Self-Attention

引入

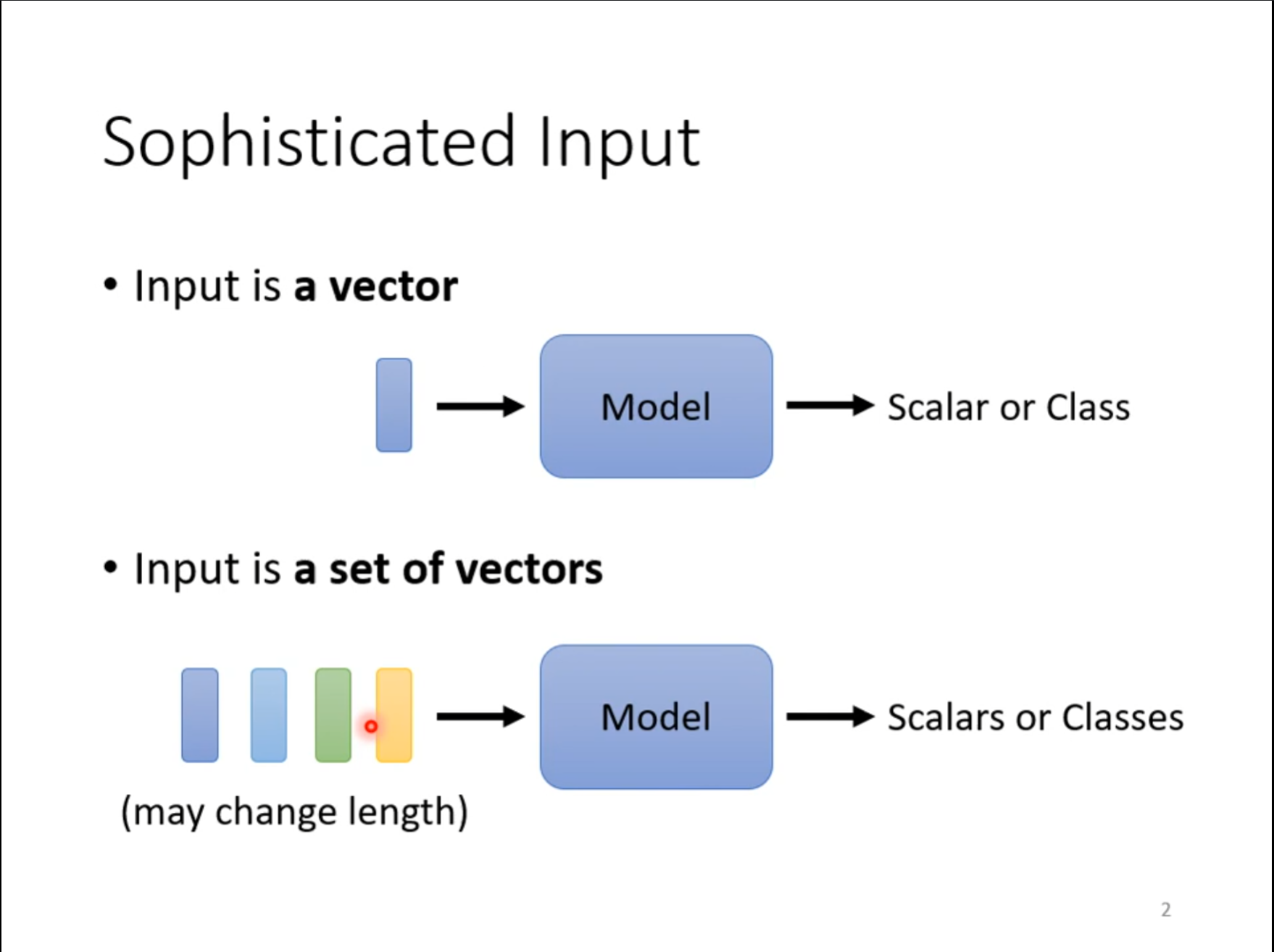
对于一个向量的输入计算我们很容易处理，但是现在我们希望对于一个句子的多个向量进行计算，这点可以体现在文字处理上。

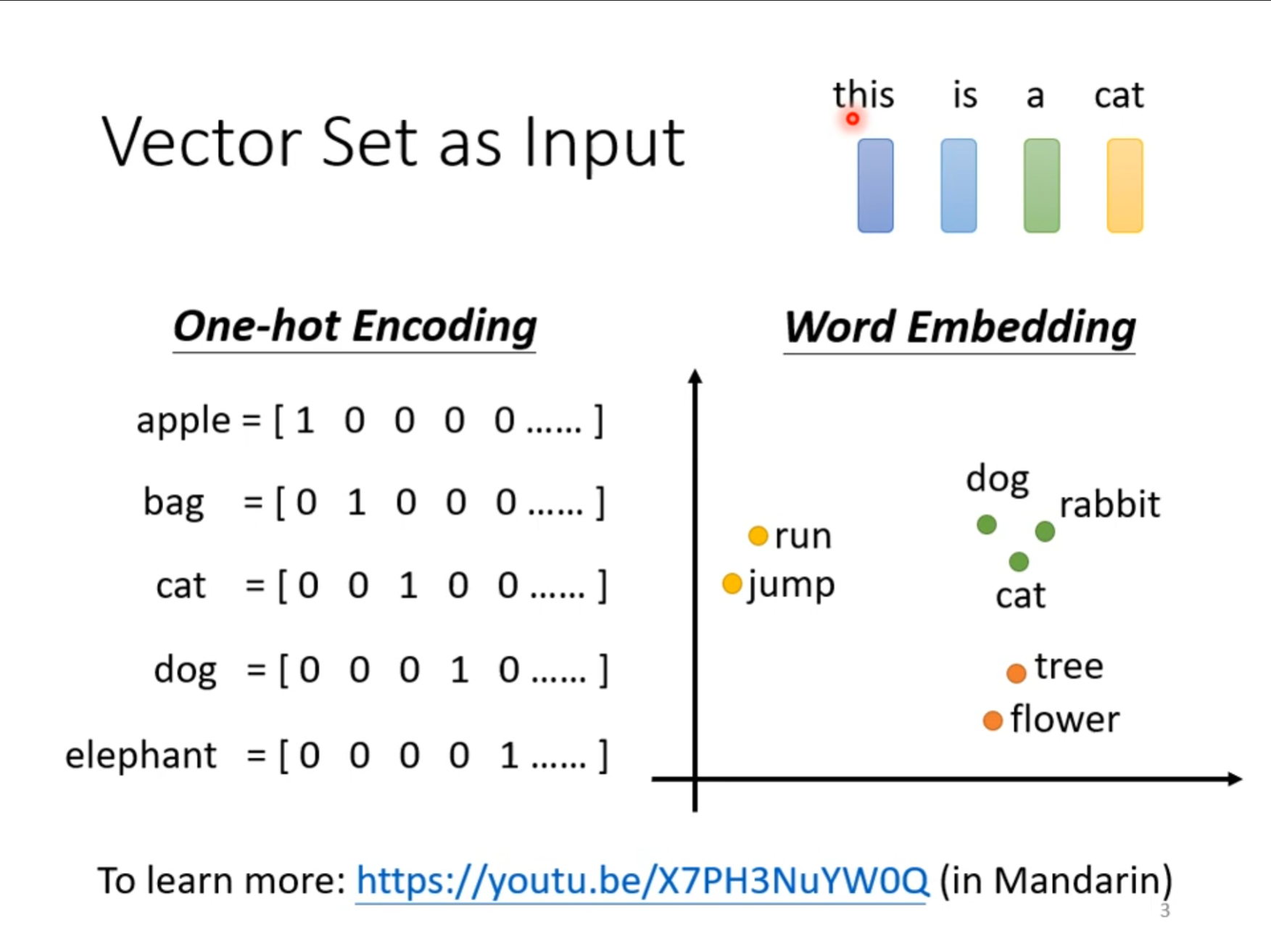
将每个单词都作为一个向量处理，那么一个句子就是多个长度不一的向量合在一起。

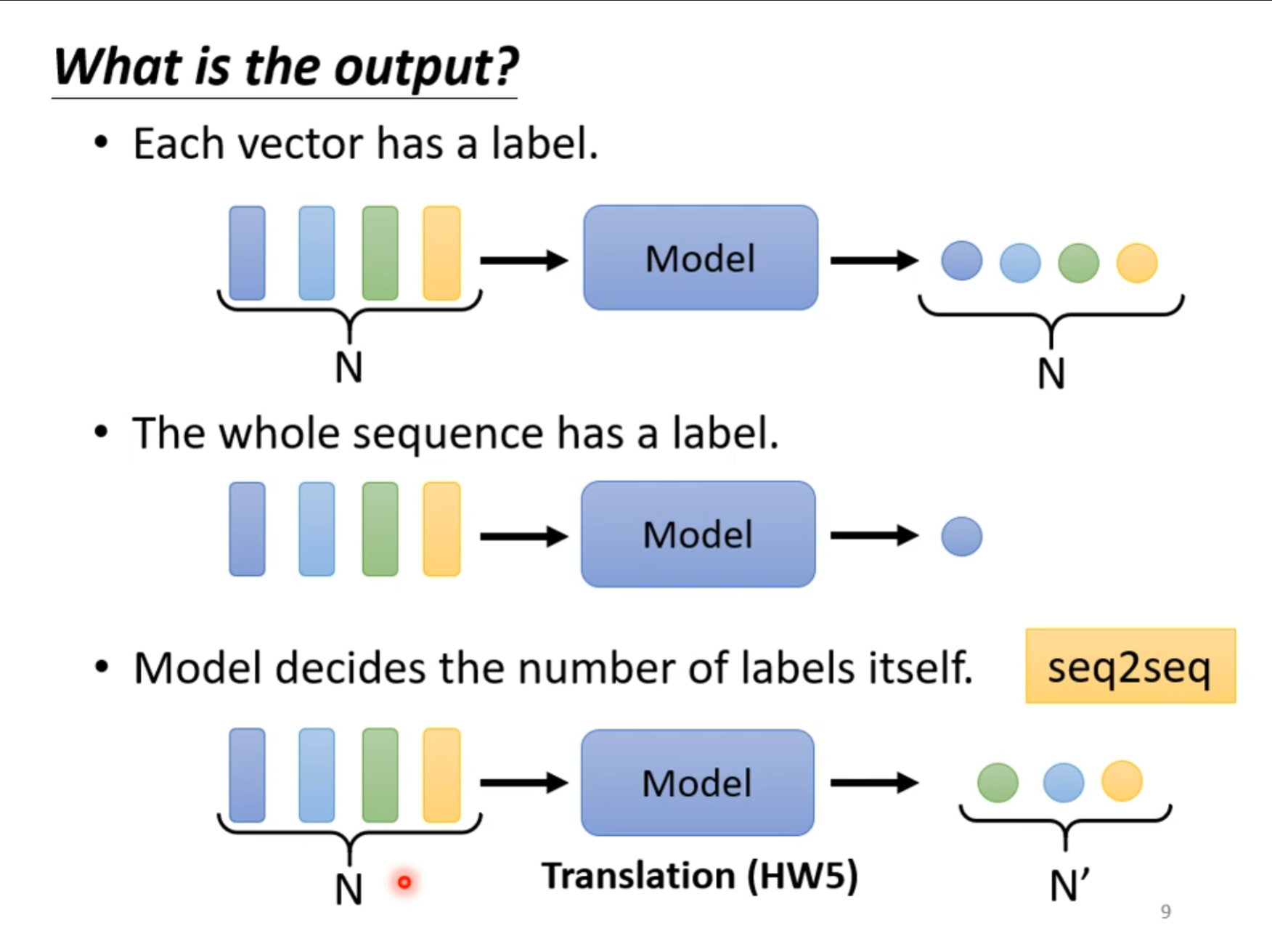
对于多个向量的输入对应的输出可能分为三种情况，每个向量对应一个标签，全部向量对应一个标签，模型自己选择输出几个标签，今天主要处理的是第一种，即一个向量对应一个标签。

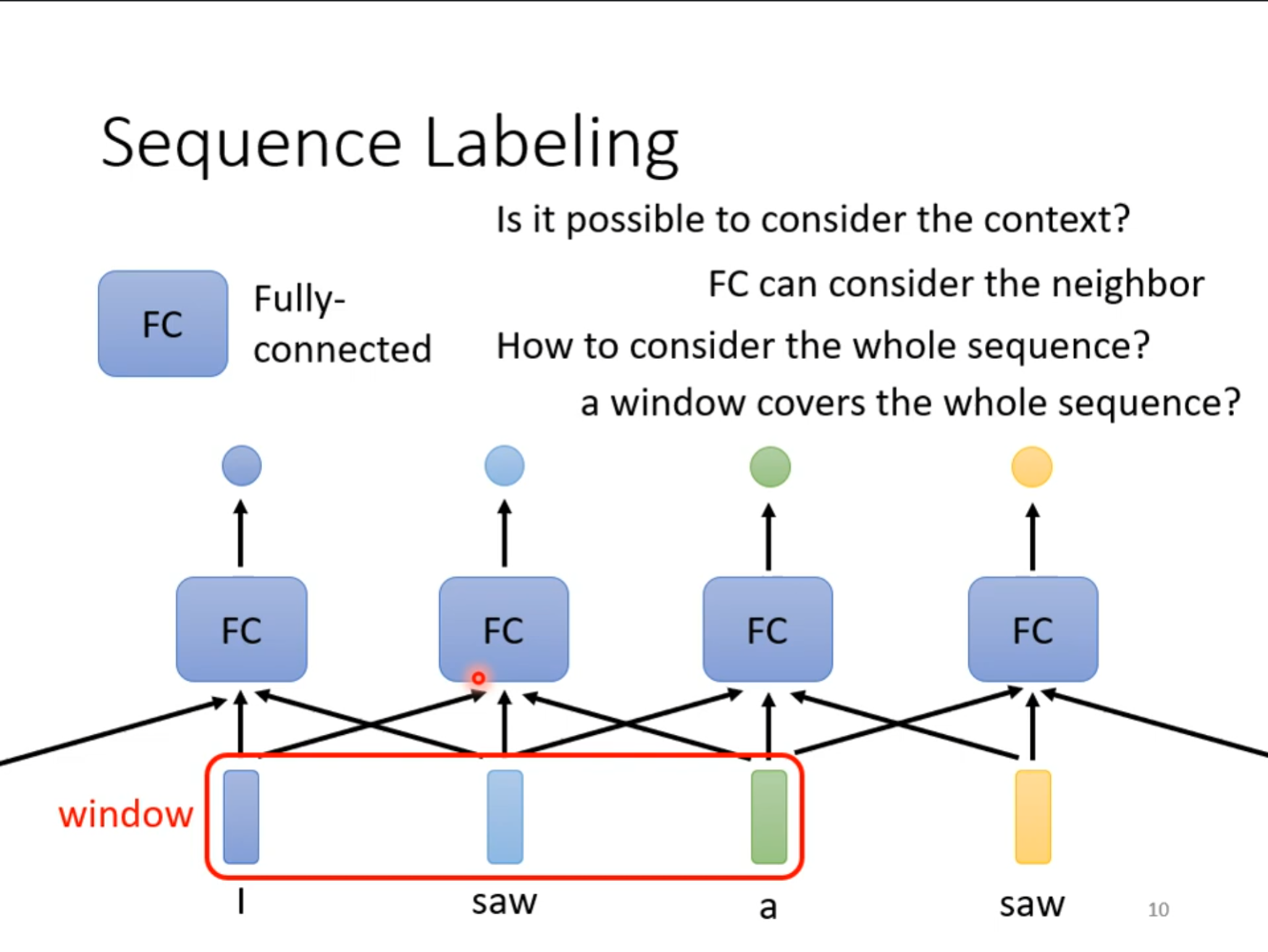
对于多个向量要想同时考虑到，可以使用一个$ window $，但是这不是最好的，因为这个窗口的大小是不固定，无法考虑到全部的向量，对于这种情况可以使用$ Self-Attention $。

Self-Attention

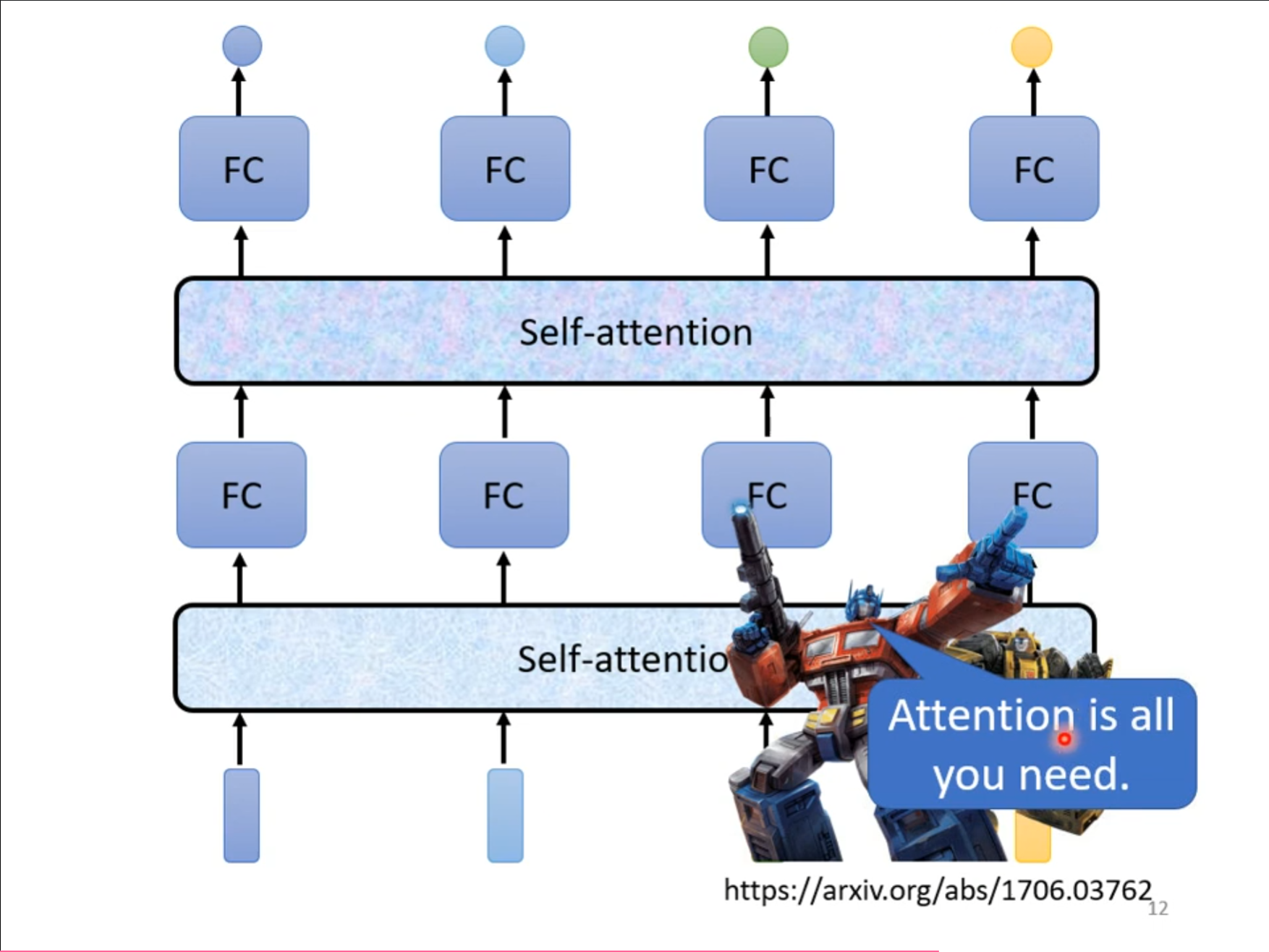
我们可以多次使用$ self-attention $，然后配合上全连接网络使用，这个也被称为自注意力机制。

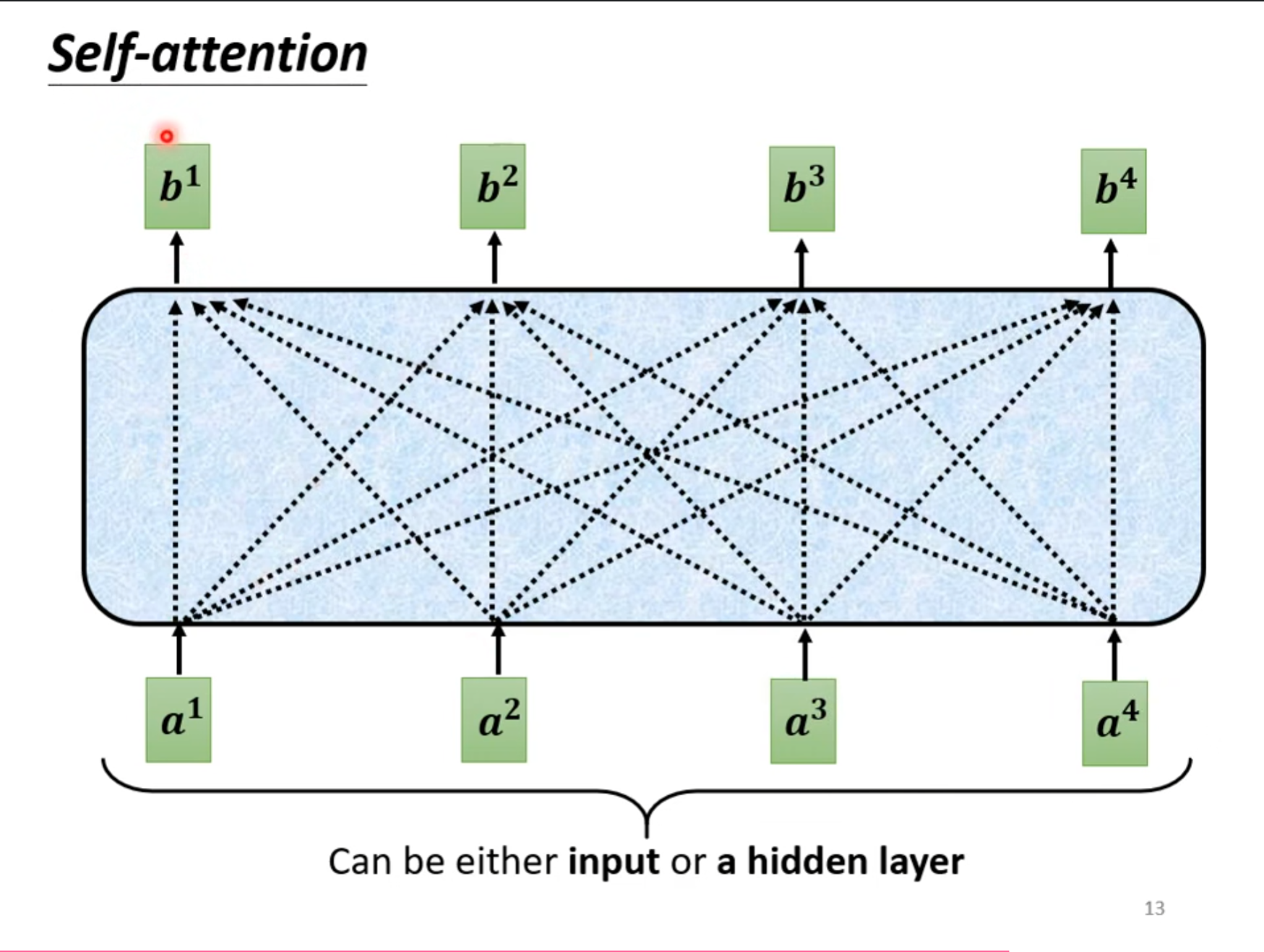
我们希望计算$ b^1 $的时候可以对于$ a^1 $同时考虑到$ a^2,a^3,a^4 $，因此我们需要知道他们彼此之间的关联性。

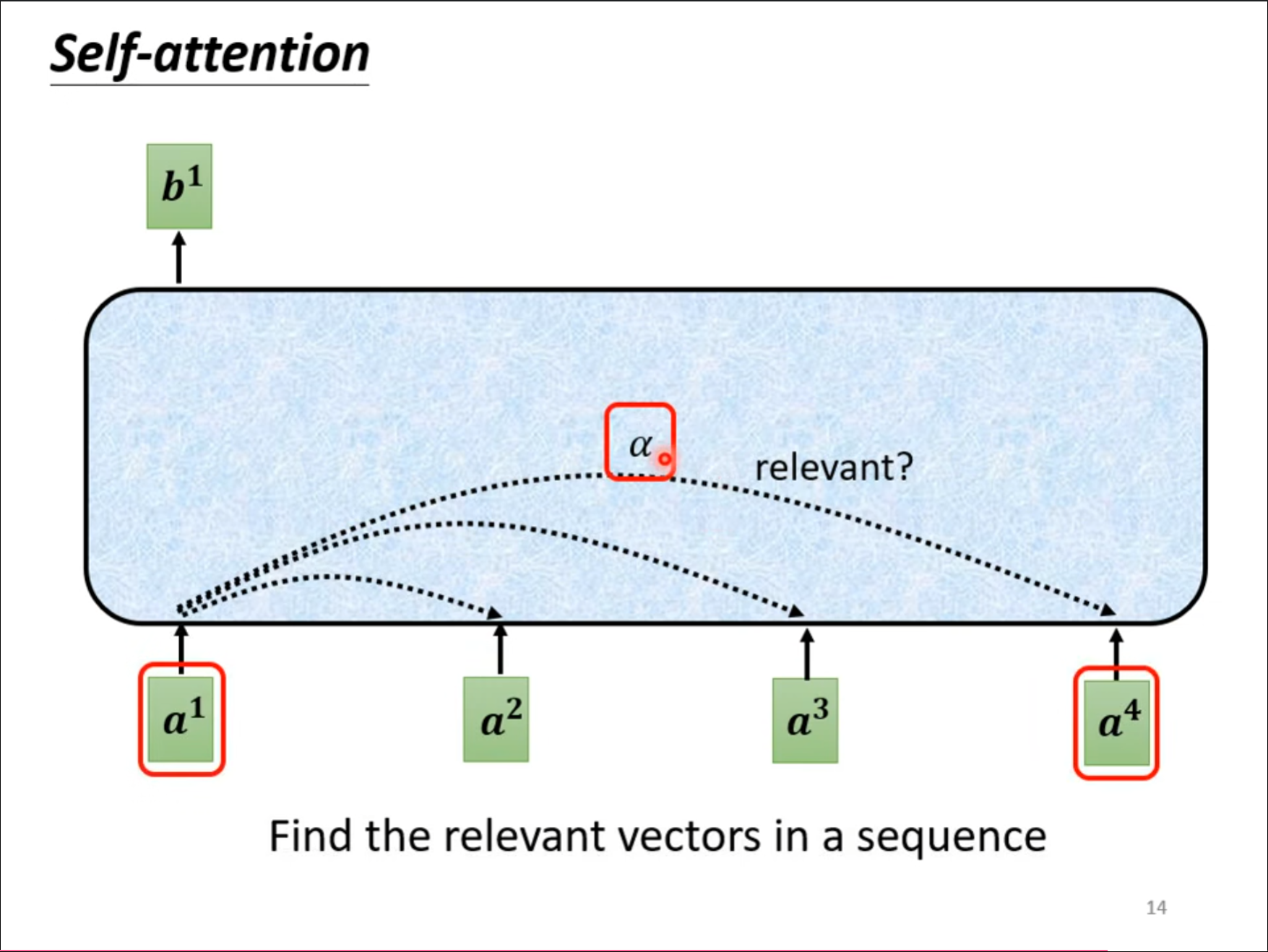
也就是使用一个$ \alpha $来计算其中的关联性，对于这个$ \alpha $的计算方法有很多种，这里提到了其中两种。

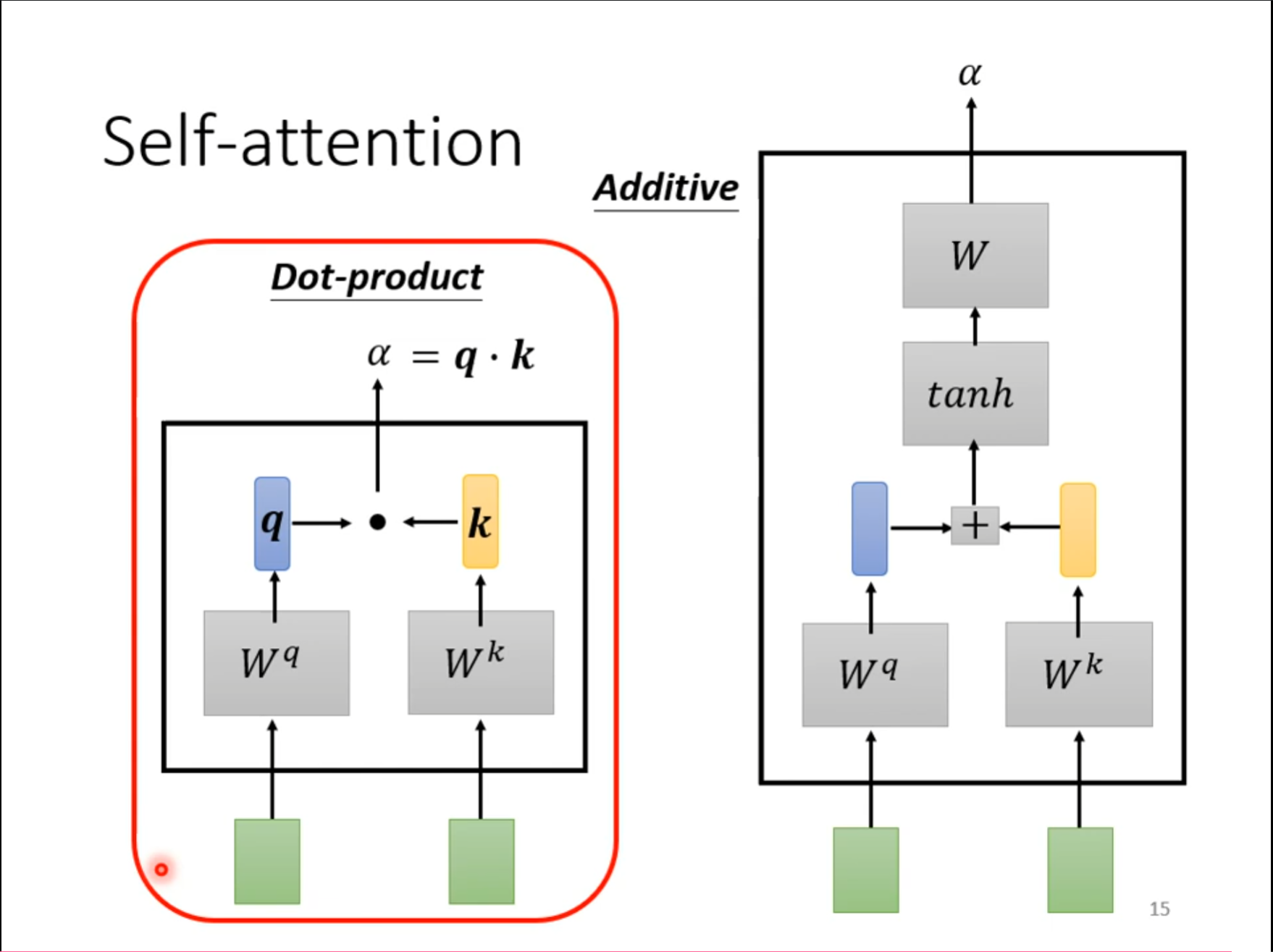
第一种是$ Dot-product $，先通过两个矩阵的变换再进行点乘，再$ self-attention $中使用的也是这个。第二种是$ Additive $，本次并没有使用。

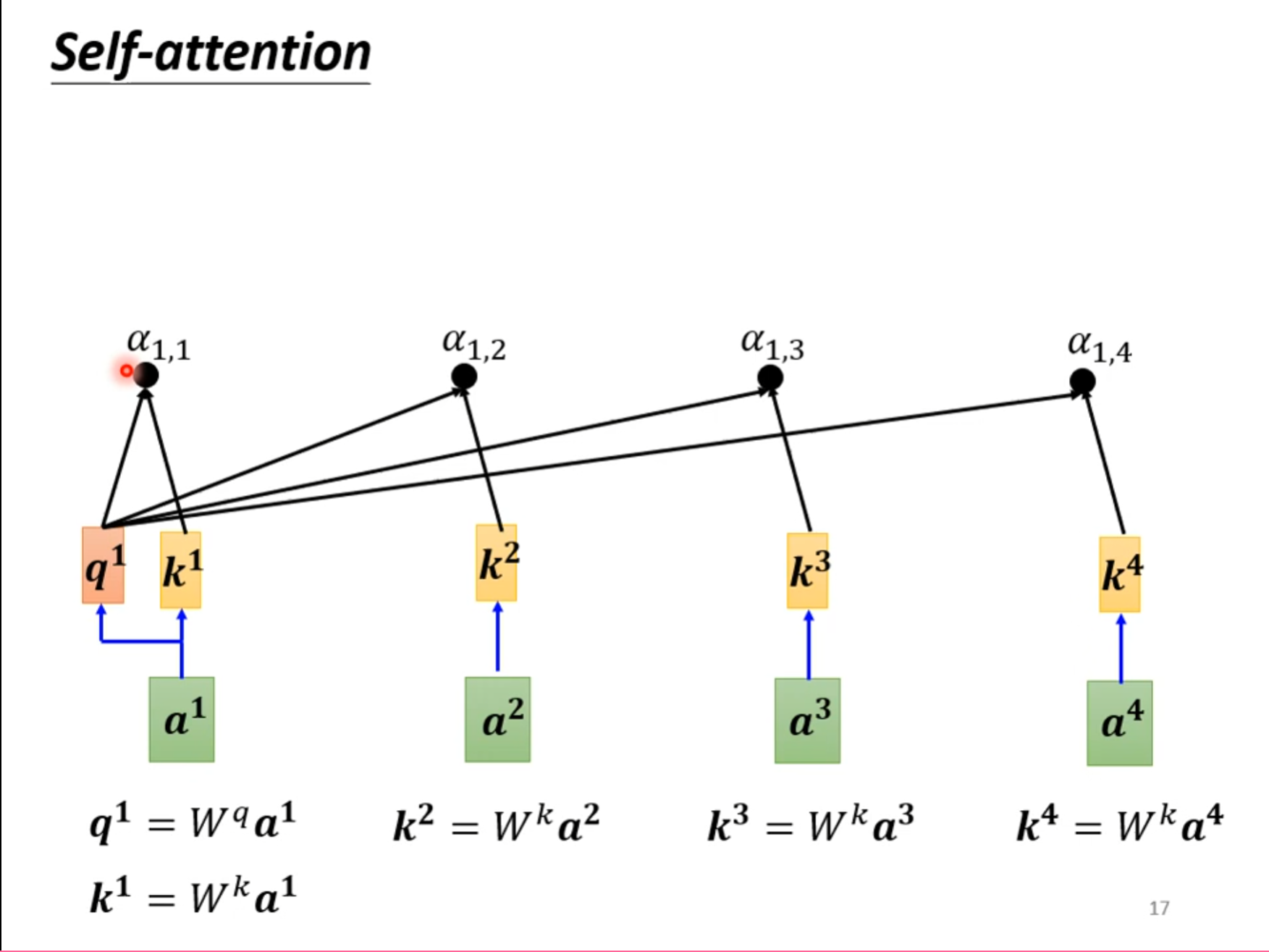
首先使用刚才的$ Dot-product $计算$ a^1 $和它本身以及其余三个的关联性。

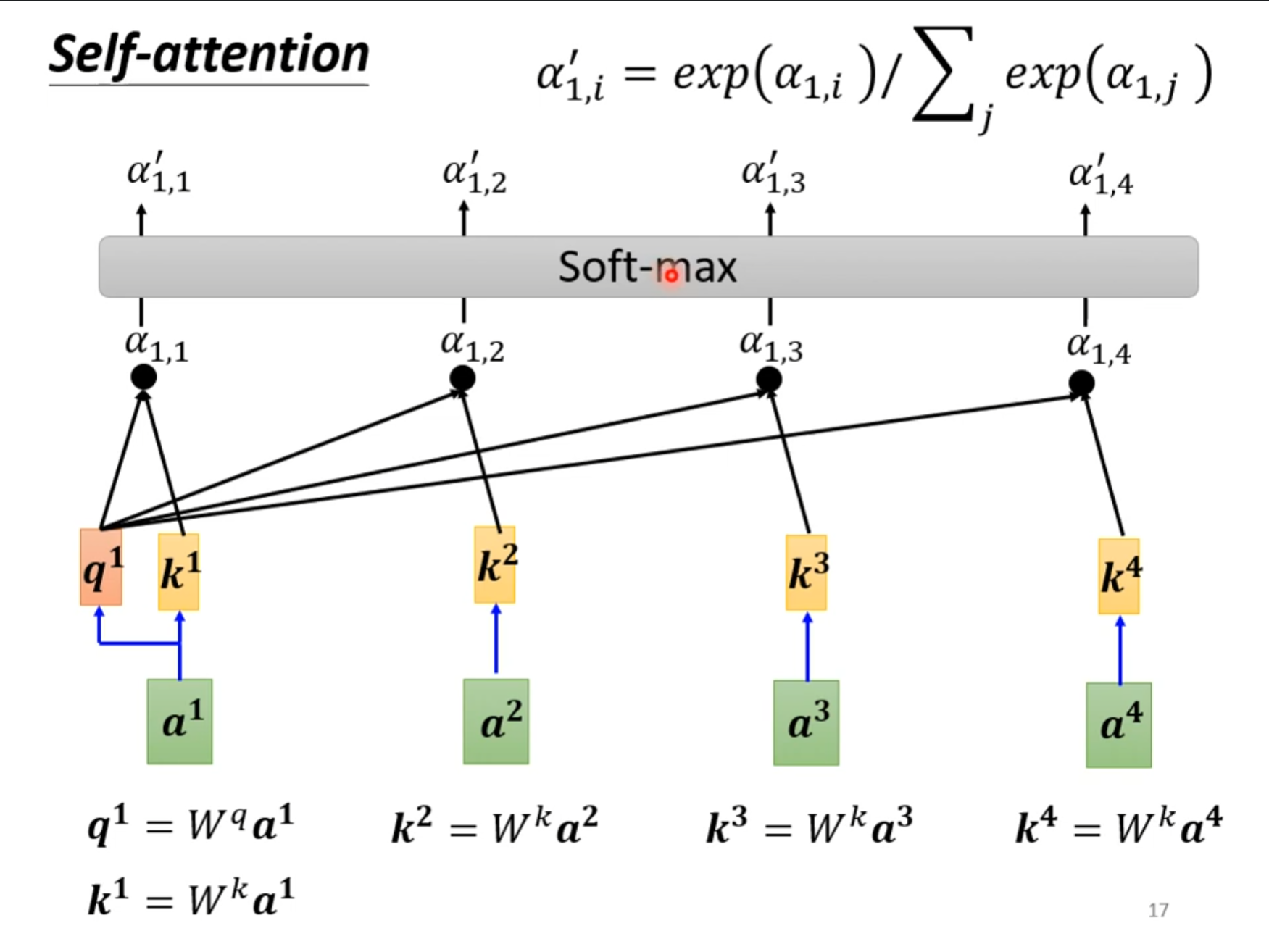
接着可以对输出的结果进行$ soft-max $，并不是一定要使用$ soft-max $，也可以使用$ relu $之类的方式。

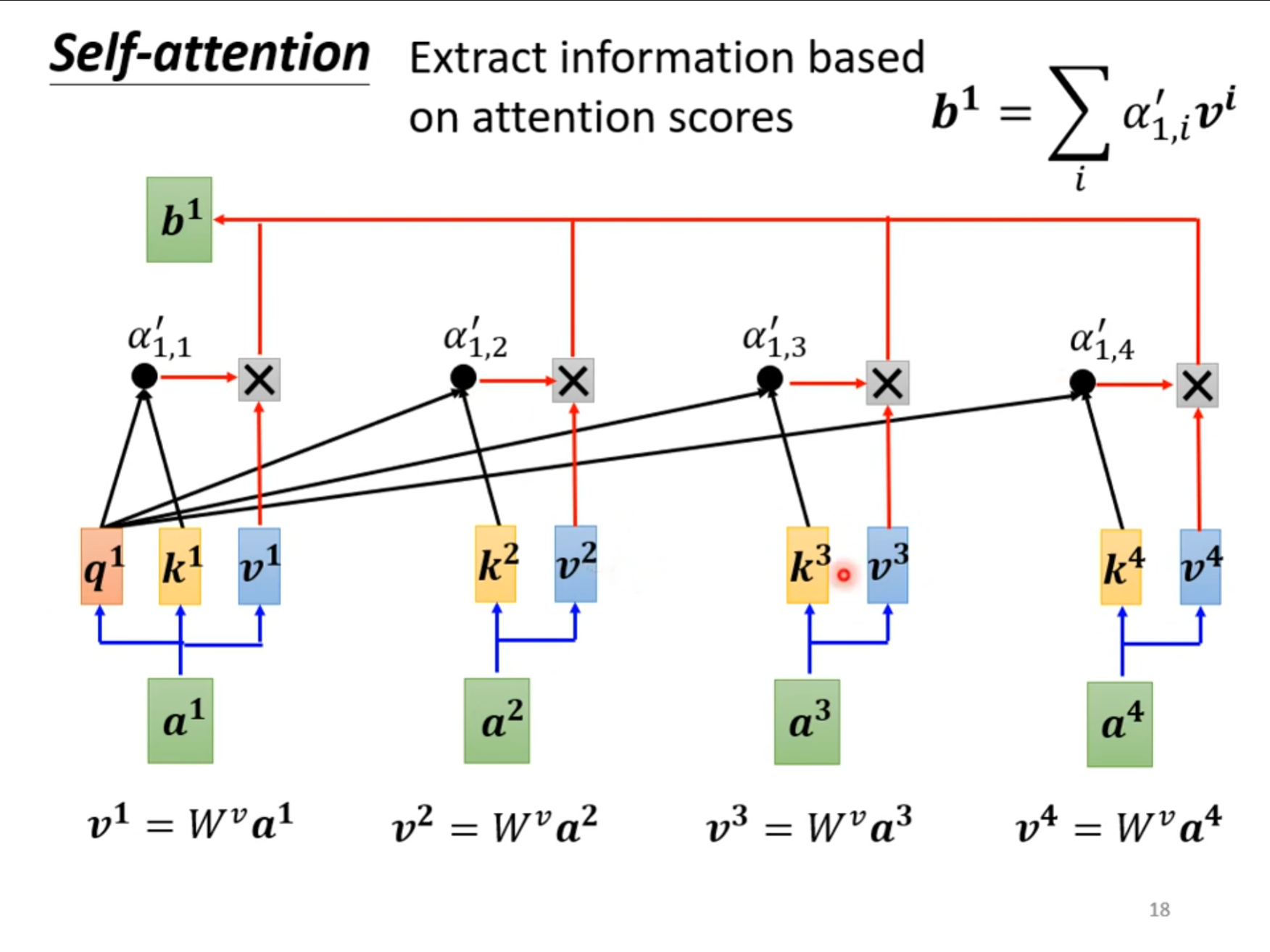
最后使用进行变化的结果和向量$ v $相乘，最后将相乘的结果加在一起就得到了$ b^1 $。

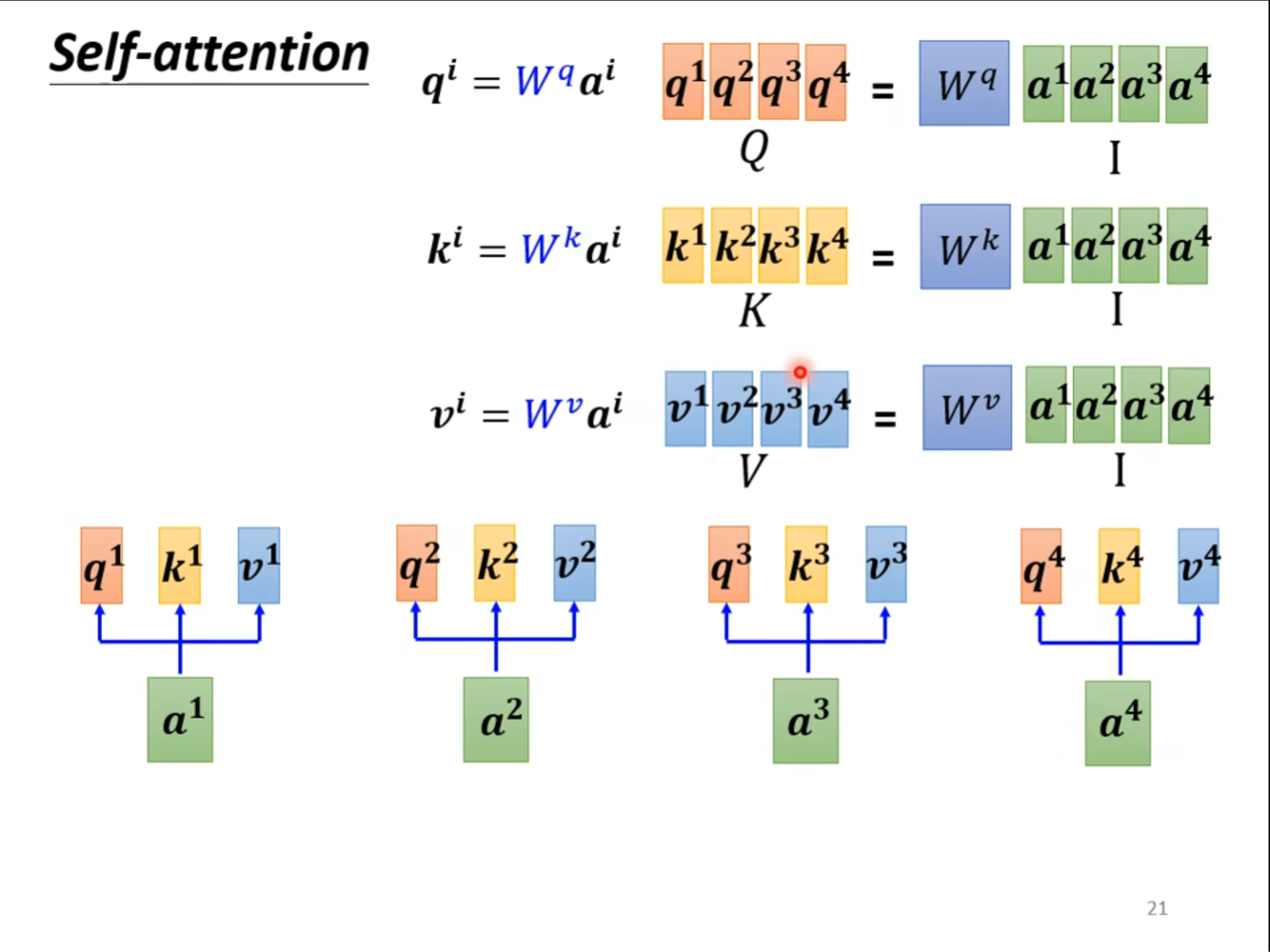
刚才介绍了怎么得到$ b^1 $的方式，现在从矩阵乘法的角度重新介绍一下，可以看到将合在一起的矩阵$ I $乘上三个不同的矩阵，就可以得到$ Q,K,V $这三个矩阵。

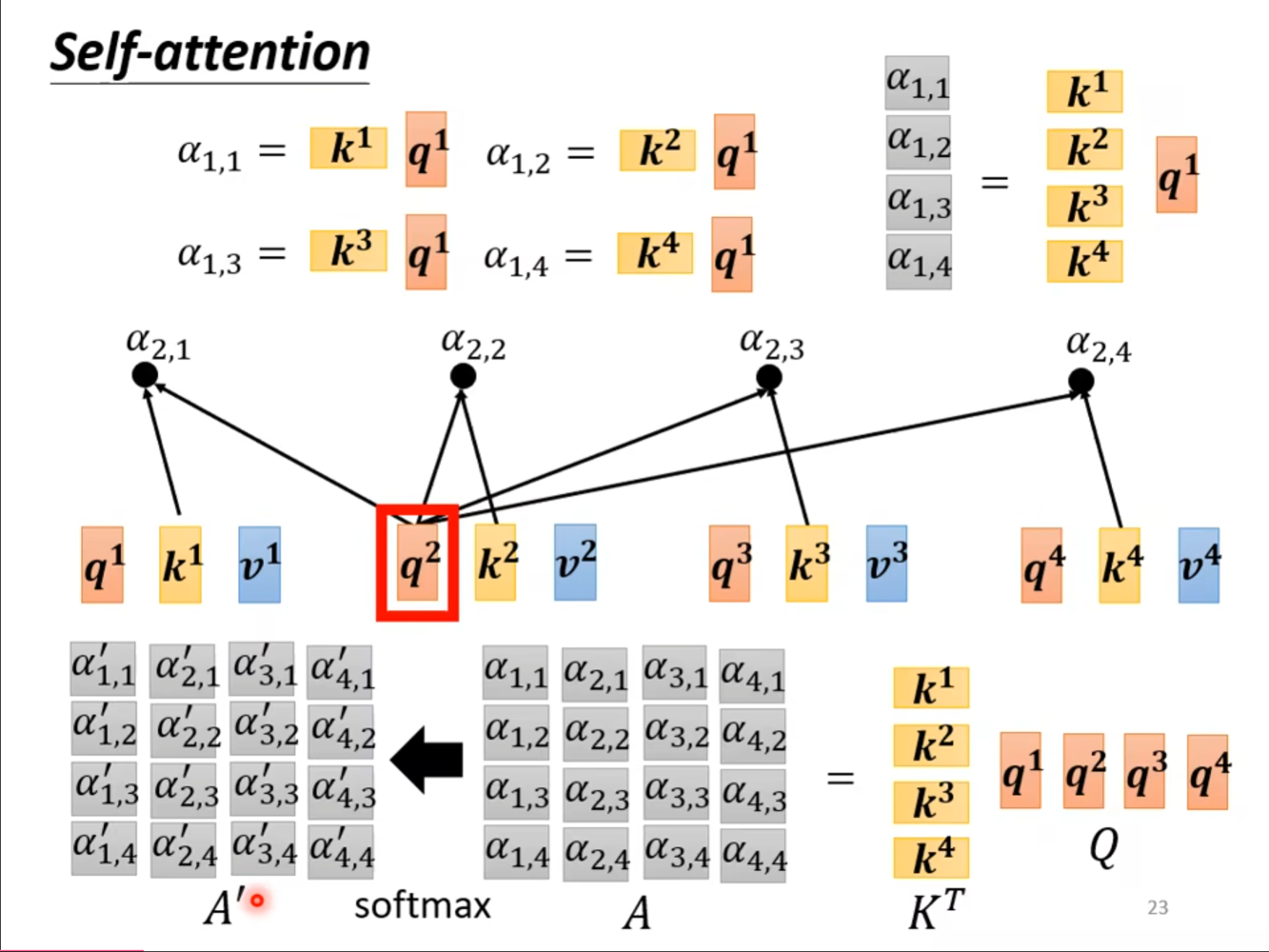
使用得到的矩阵$ K $的转置和矩阵$ Q $相乘，就可以得到矩阵$ A $，通过$ soft-max $就可以得到$ {A’} $

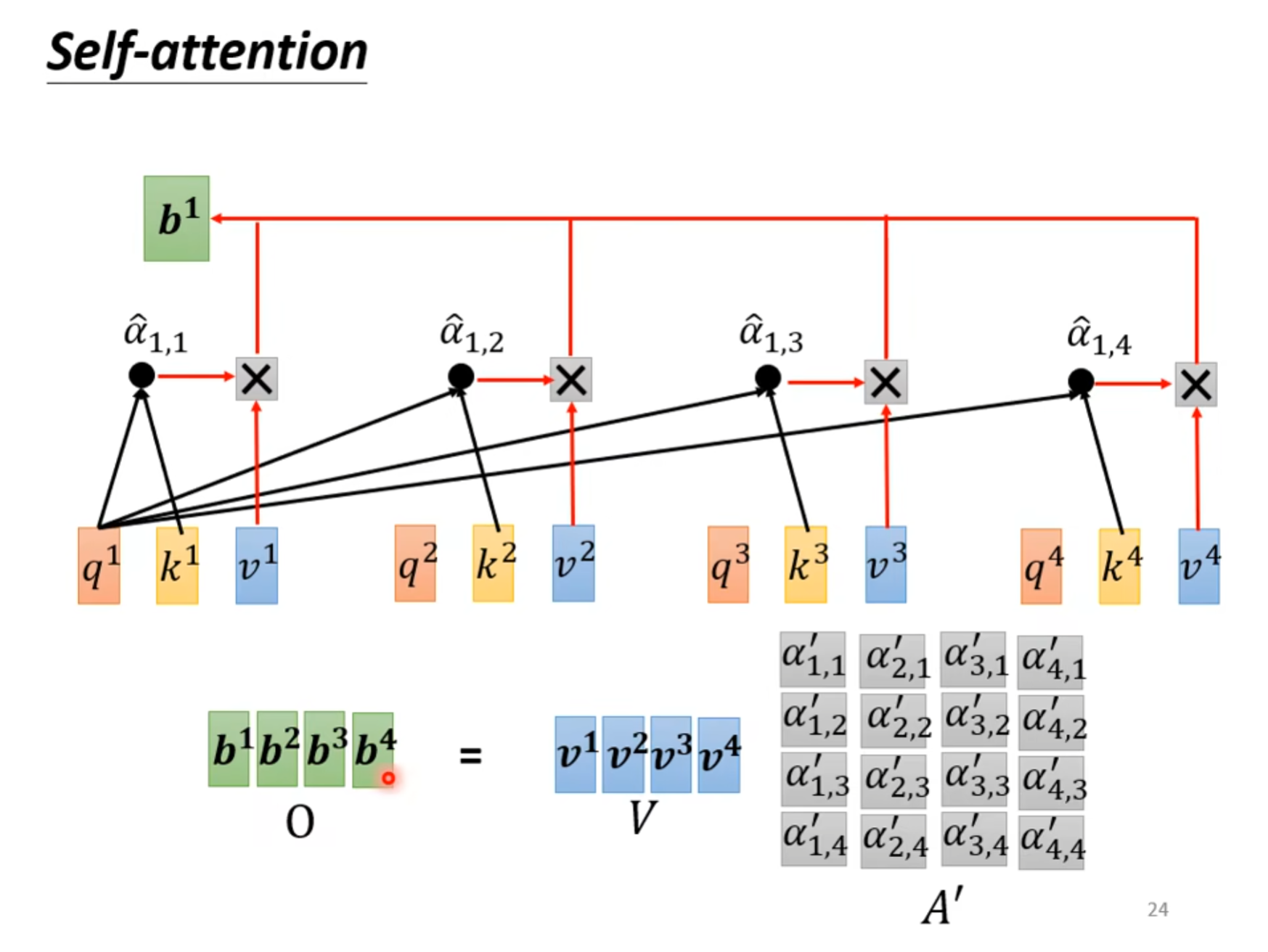
将得到的矩阵$ {A’} $和$ V $相乘就可以得到我们的输出向量$ O $，其实刚才的操作就是矩阵的相乘。

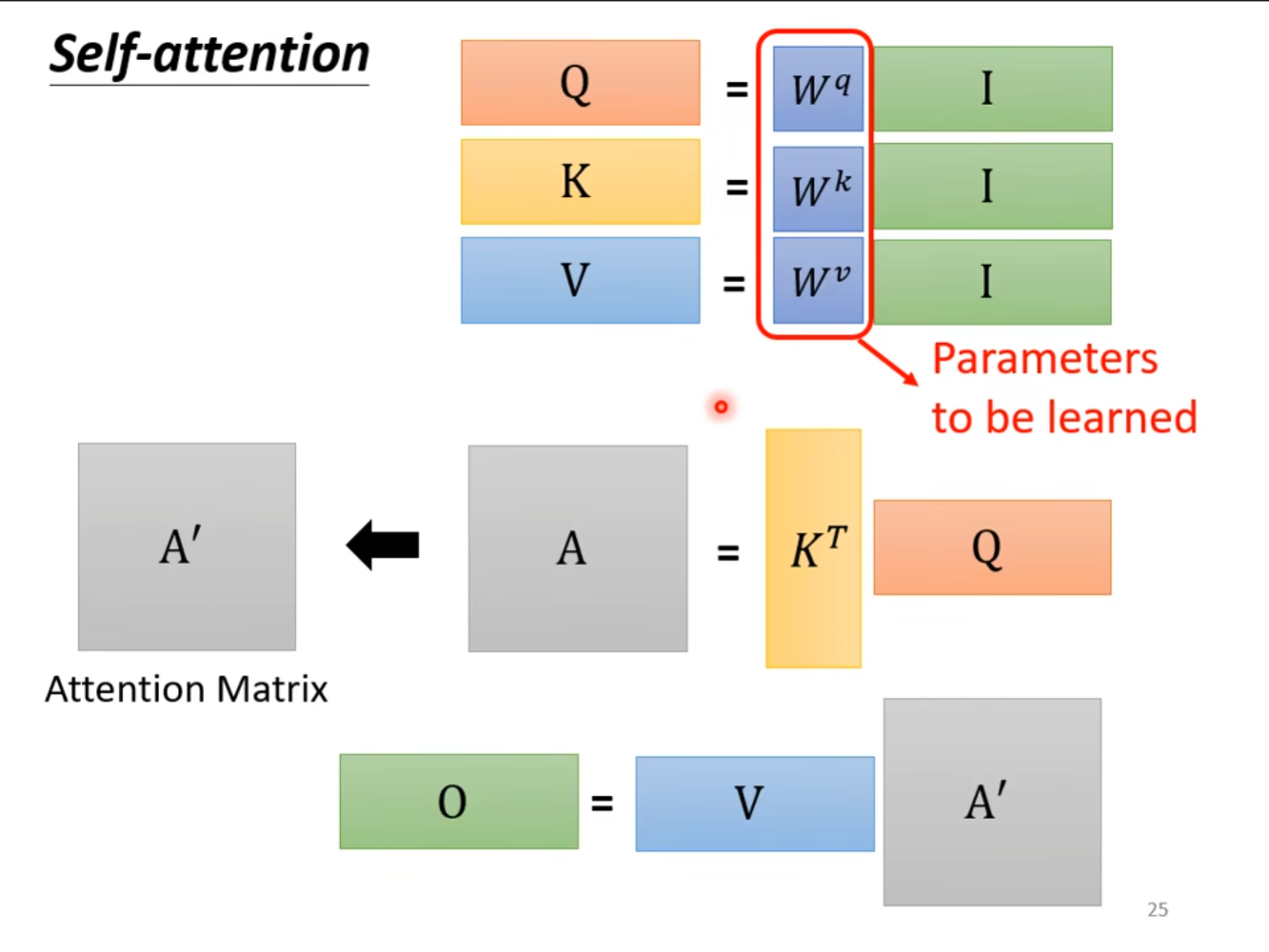
上图中从$ I $到$ O $的改变就是做的$ self-attention $的操作，其中就只有$ W^q,W^k,W^v $这三个矩阵参数是需要我们学习的。

多头自注意力机制

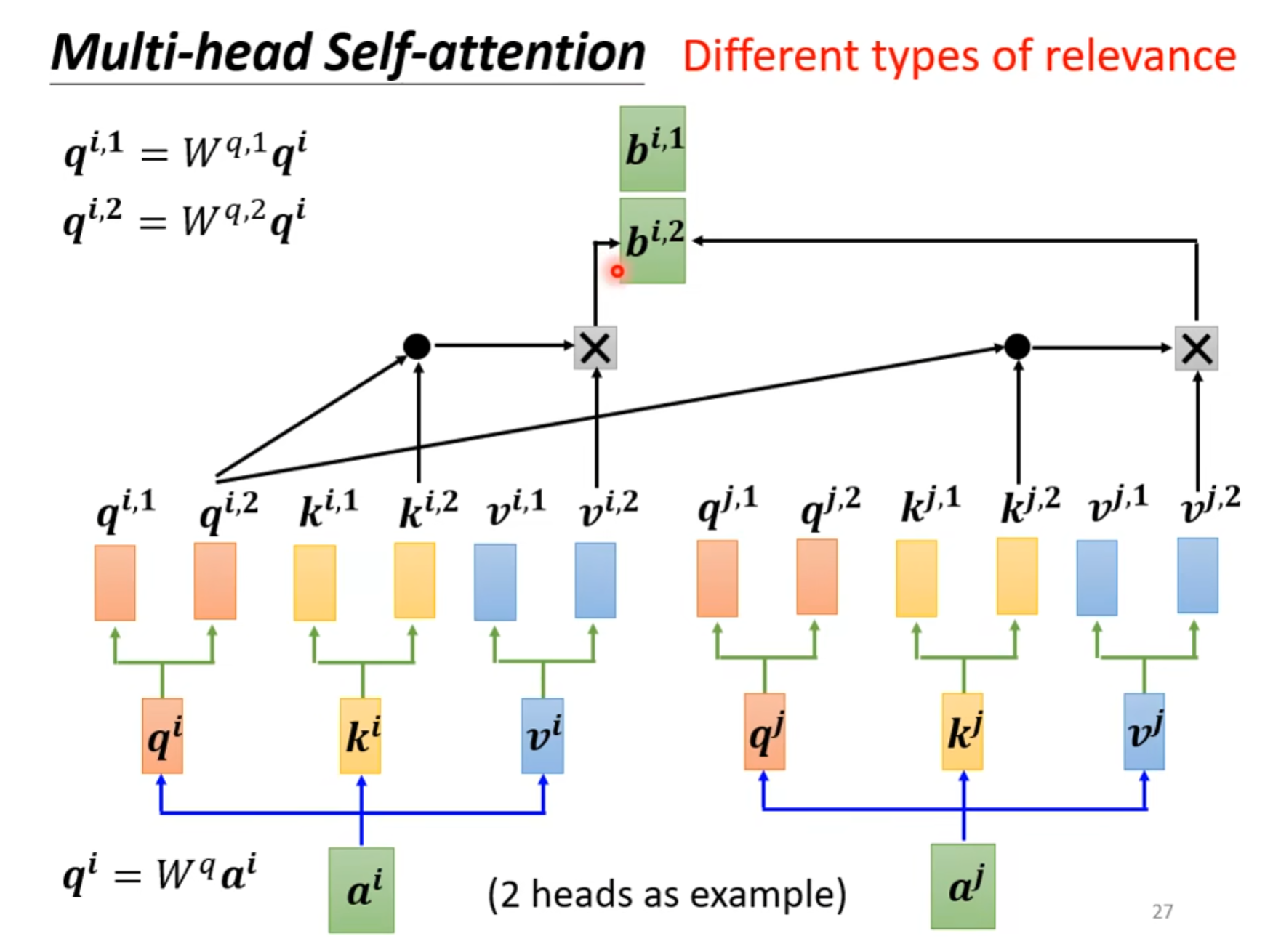
在计算相关性的时候可能不仅只有一种相关性，因此我们可以将$ q^i,k^i,v^i $的值都再乘不同的两个矩阵，最终可以得到两个$ b^{i,1},b^{i,2} $。

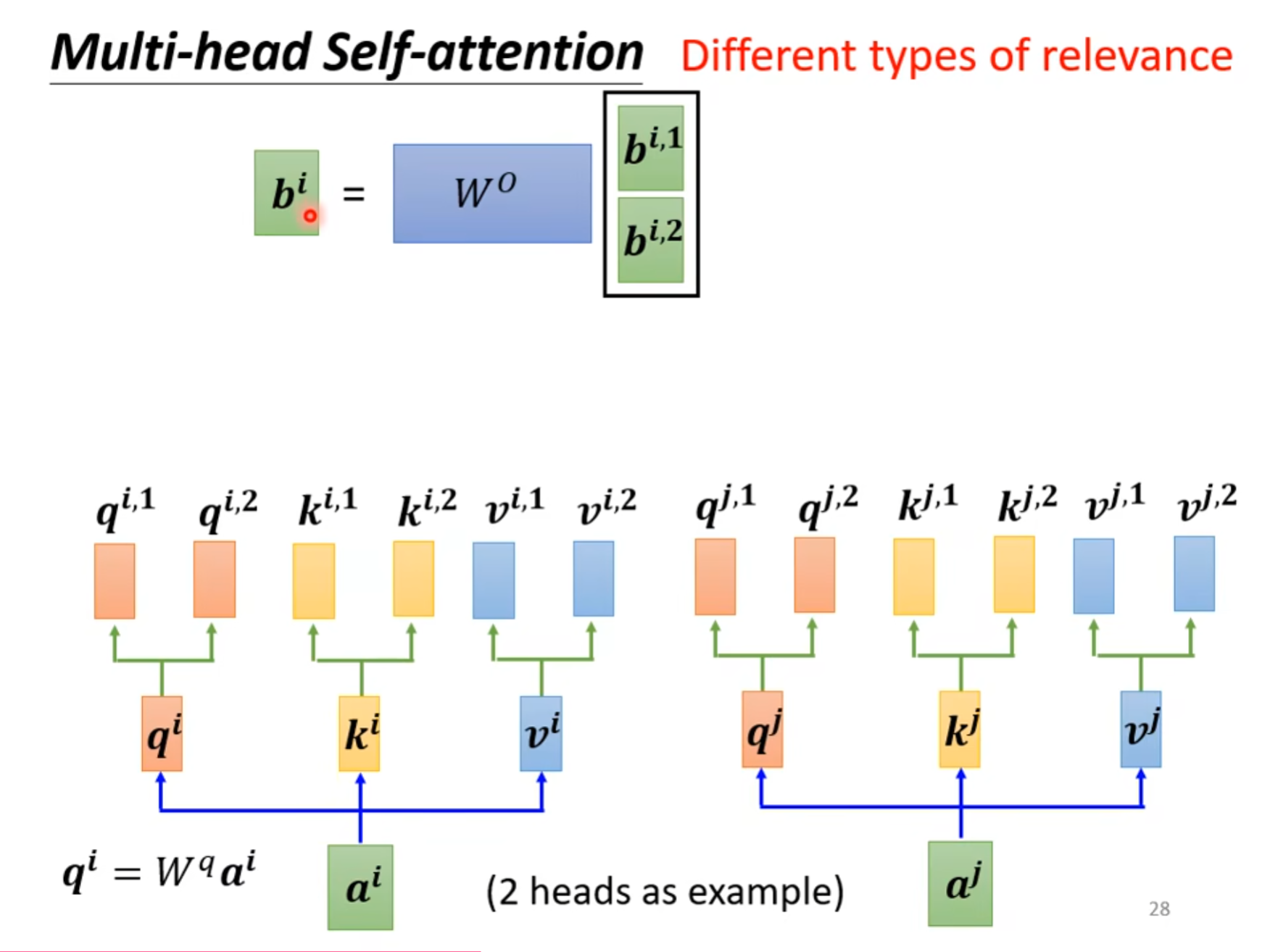
最后乘上一个$ W^o $的向量，可以得到一个$ b^i $的值。

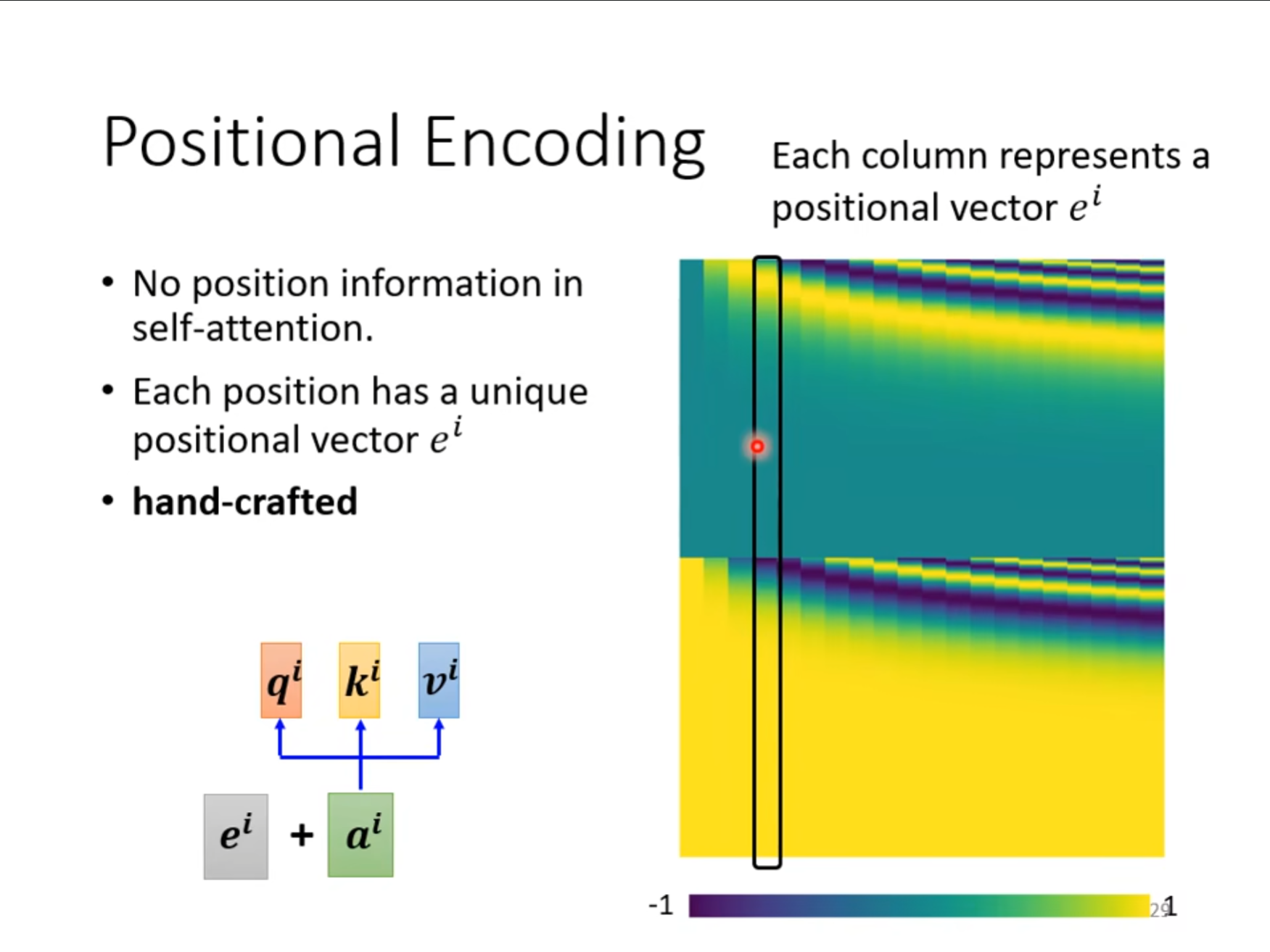
刚才的计算中还存在一个问题，我们没有考虑向量之间的位置关系，不同的位置的影响没有被考虑进来，为了解决这个问题，我们可以计算每个位置对应的向量，将这个向量和$ a^i $相加进行计算从而将位置的信息也考虑进来。

CNN v.s. self-attention

$ CNN $和$ self-attention $之间有很强的相关性，我们可以认为$ CNN $就是一个简化版的$ self-attention $，区别在于$ self-attention $更加的灵活，让机器自己去学习和自己相关的$ pixel $，而不是人为的设置感受野，对于$ self-attention $进行一些限制就可以做到$ CNN $一样的事。

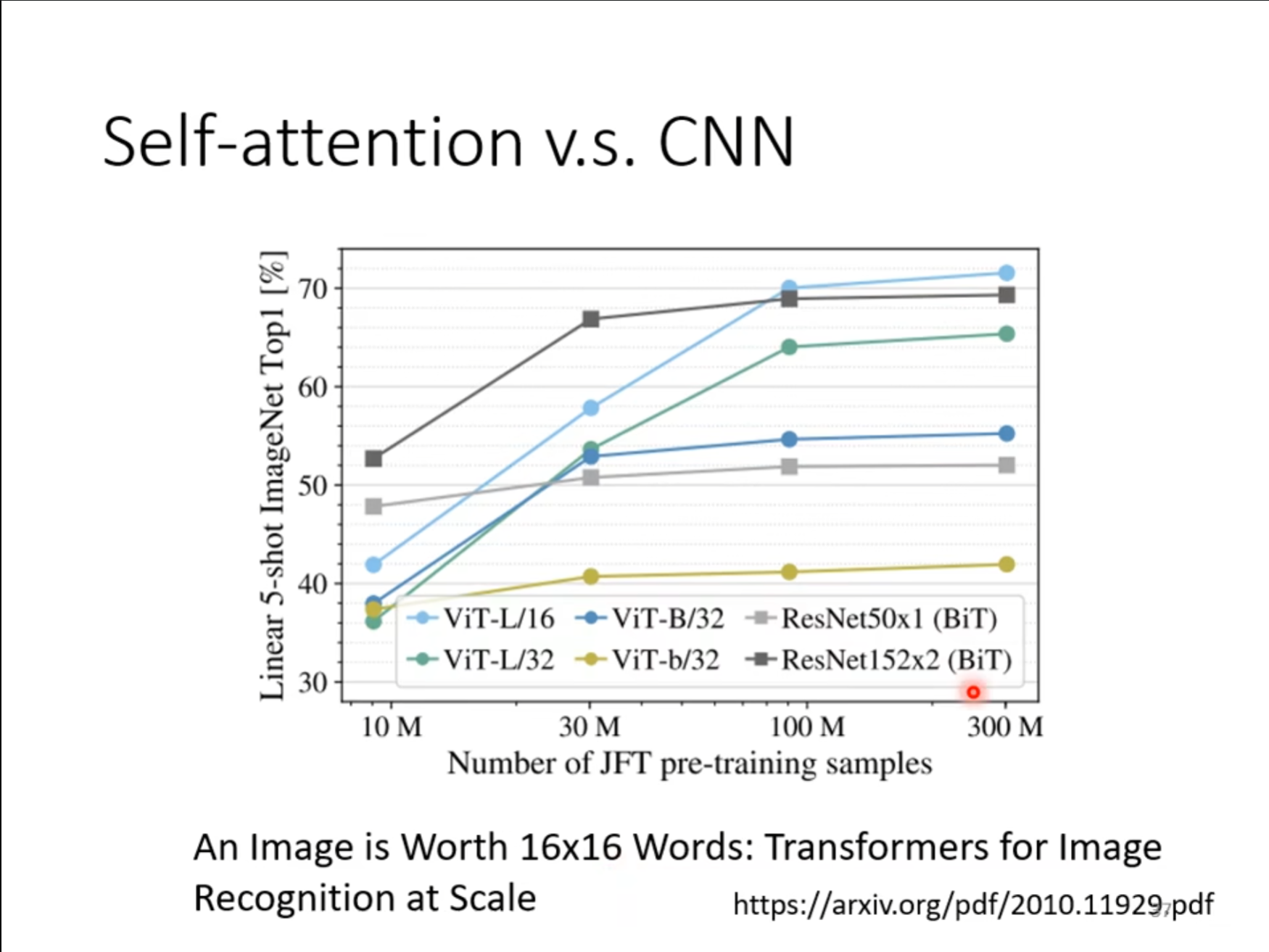
既然$ self-attention $更加的灵活，那么也就代表更加容易过拟合，因此数据量很大的时候$ self-attention $的效果是要好于$ CNN $，但数据量不足的时候$ CNN $的效果就要比$ self-attention $要好一些。

RNN v.s. self-attention

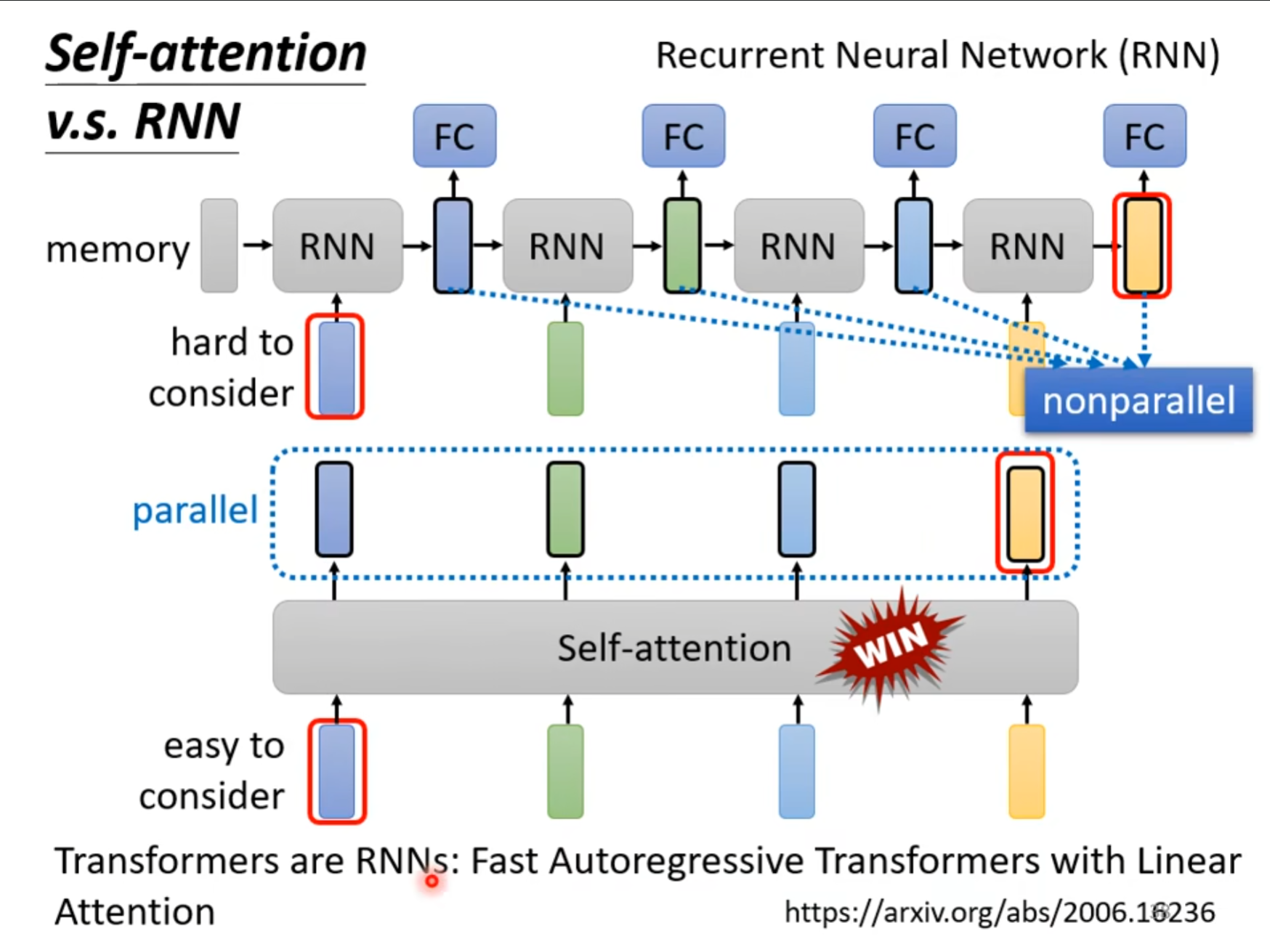
对于$ RNN $来讲，$ self-attention $虽然也都是处理多个向量的输入的，但是它并不是同时处理的，而是从左到右，在处理左边的时候无法考虑到右边，虽然也可以通过双向的$ RNN $完善，但是它也不是并行计算，因此现在更加倾向于使用$ self-attention $。

可参照：

Transformer：注意力机制（attention）和自注意力机制（self-attention）的学习总结_注意力机制和自注意力机制-CSDN博客