RNN

介绍

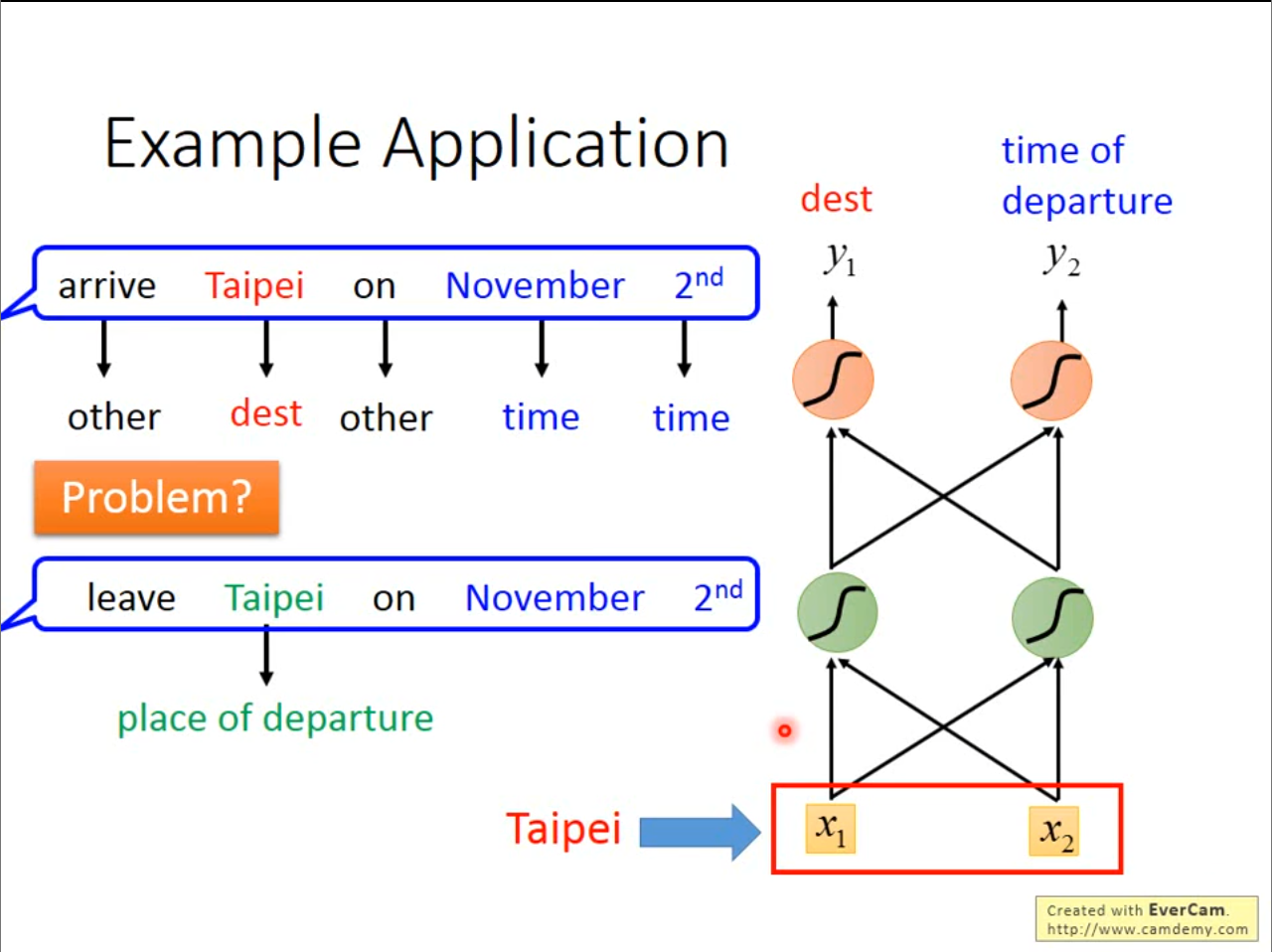
对用同一个词语在不同的话中可能具有完全相反的意思，但是如果还是使用之前神经网络，那么输入结果一定是相同的，为了解决这个问题，我们希望神经网络可以具有一些记忆性，这就是接下来要介绍的循环神经网络。

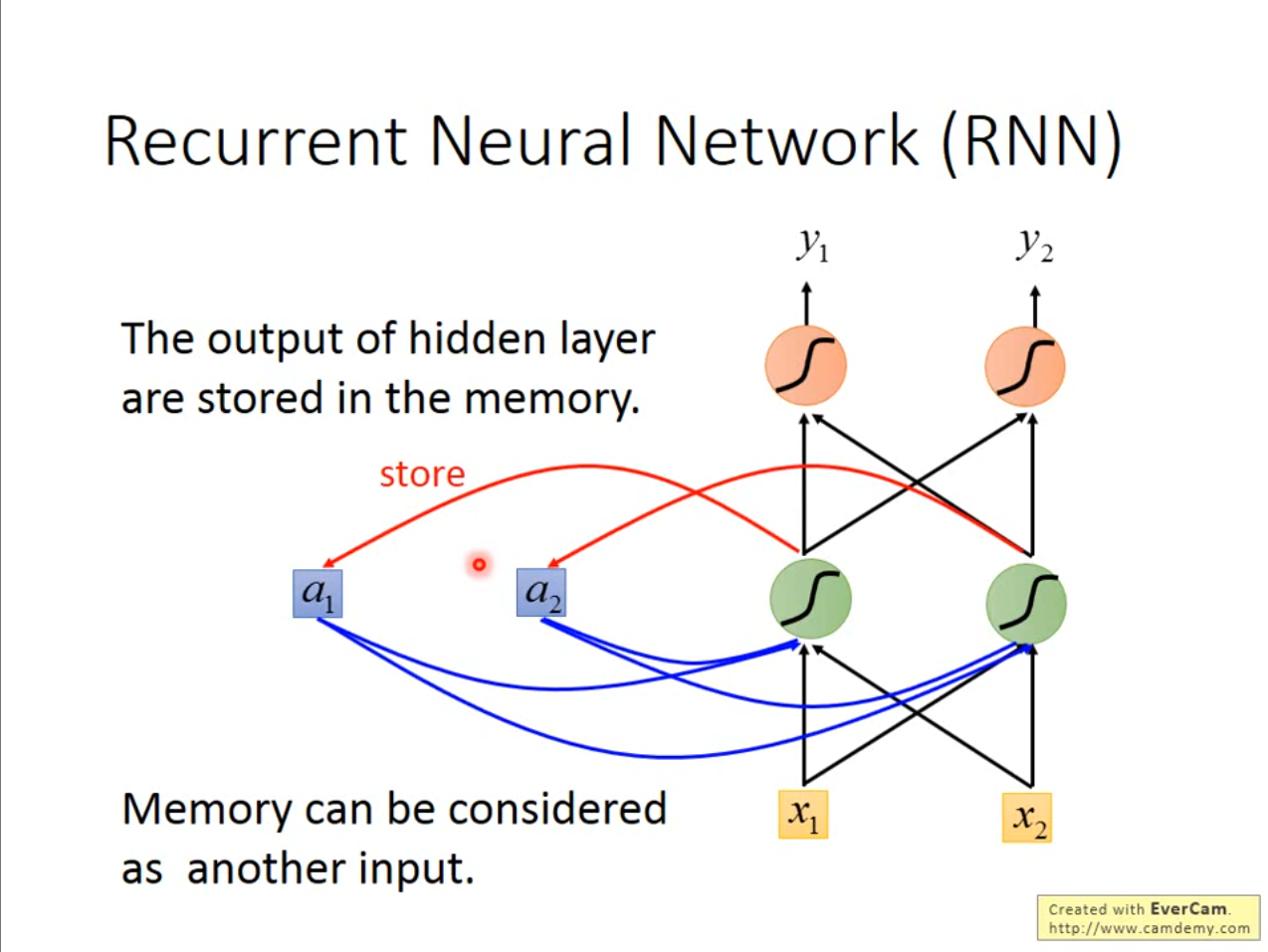
因此我们讲隐藏层的输出结果全部都放入到一个$ store $中进行存储，在下次输入中再取出来进行使用。

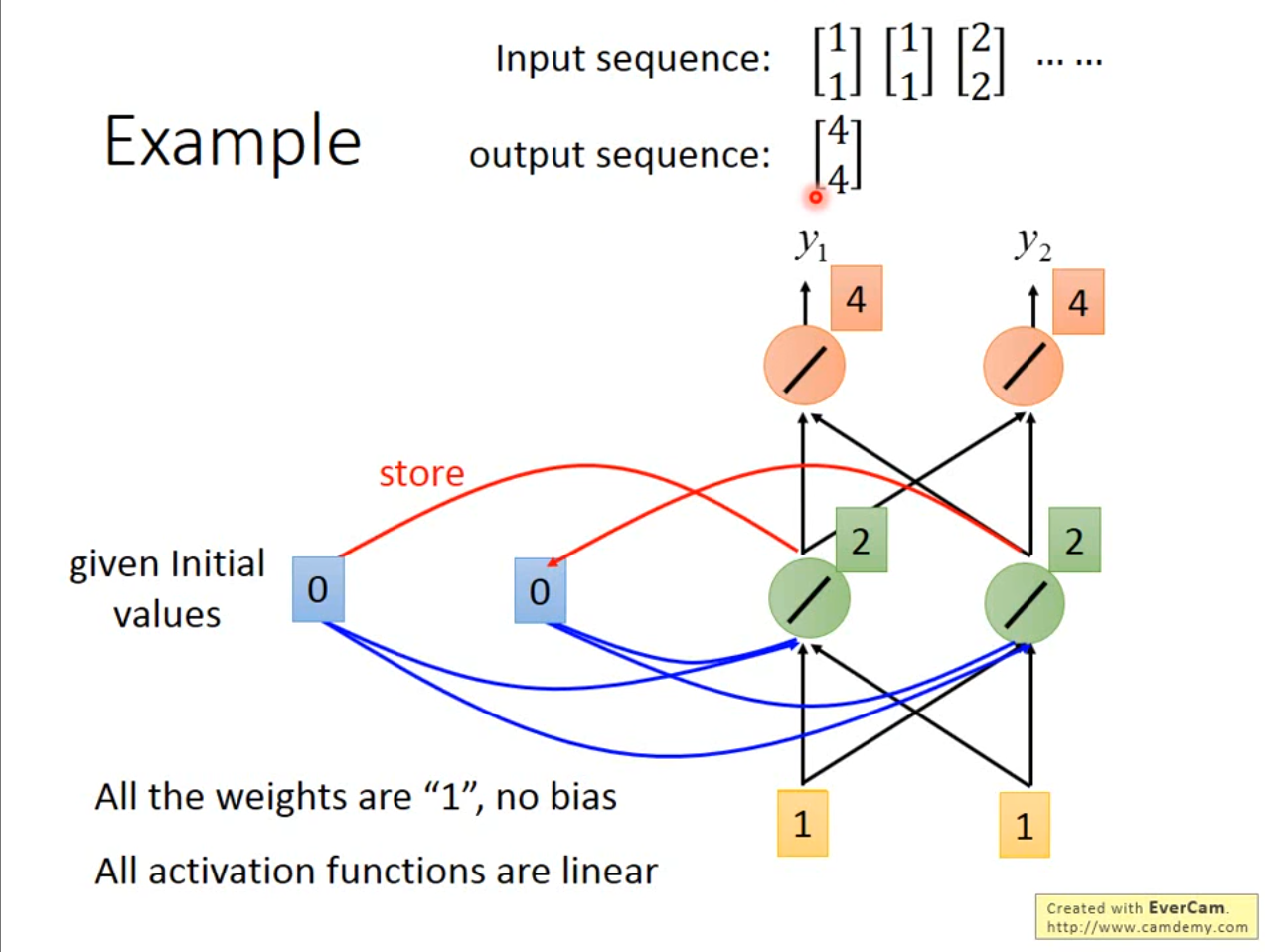
用一个例子解释，当输入为$ [1,1] $，权重为$ 1 $，无偏置的情况，第一次的输出就是$ [4,4] $，同时隐藏层的$ [2,2] $存储在$ store $中。

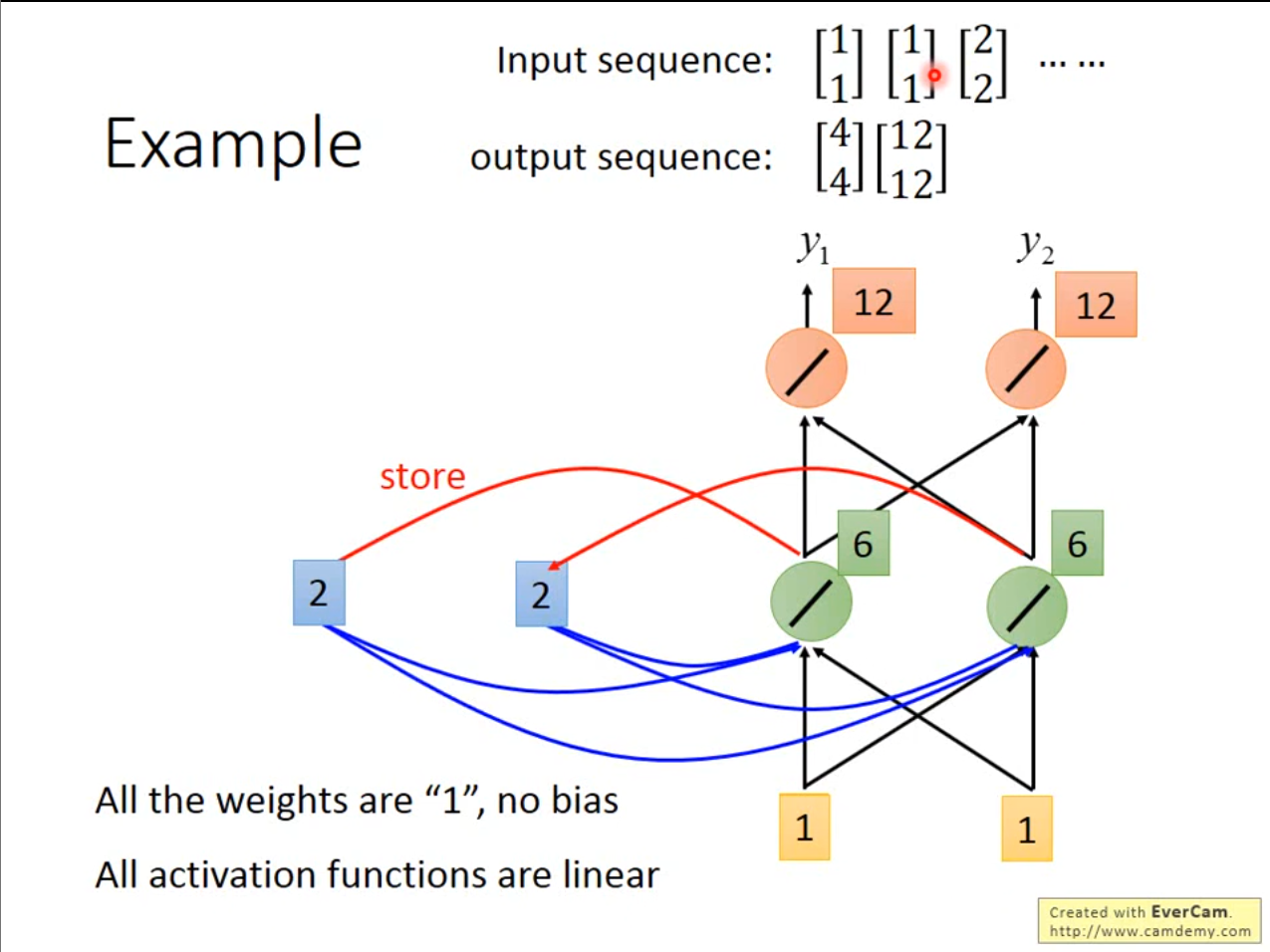
在第二次中，使用了上一次的存储值，因此就是相当于有四个输入$ 1,1,2,2 $因此最终即使输入相同，但是输出也不同。

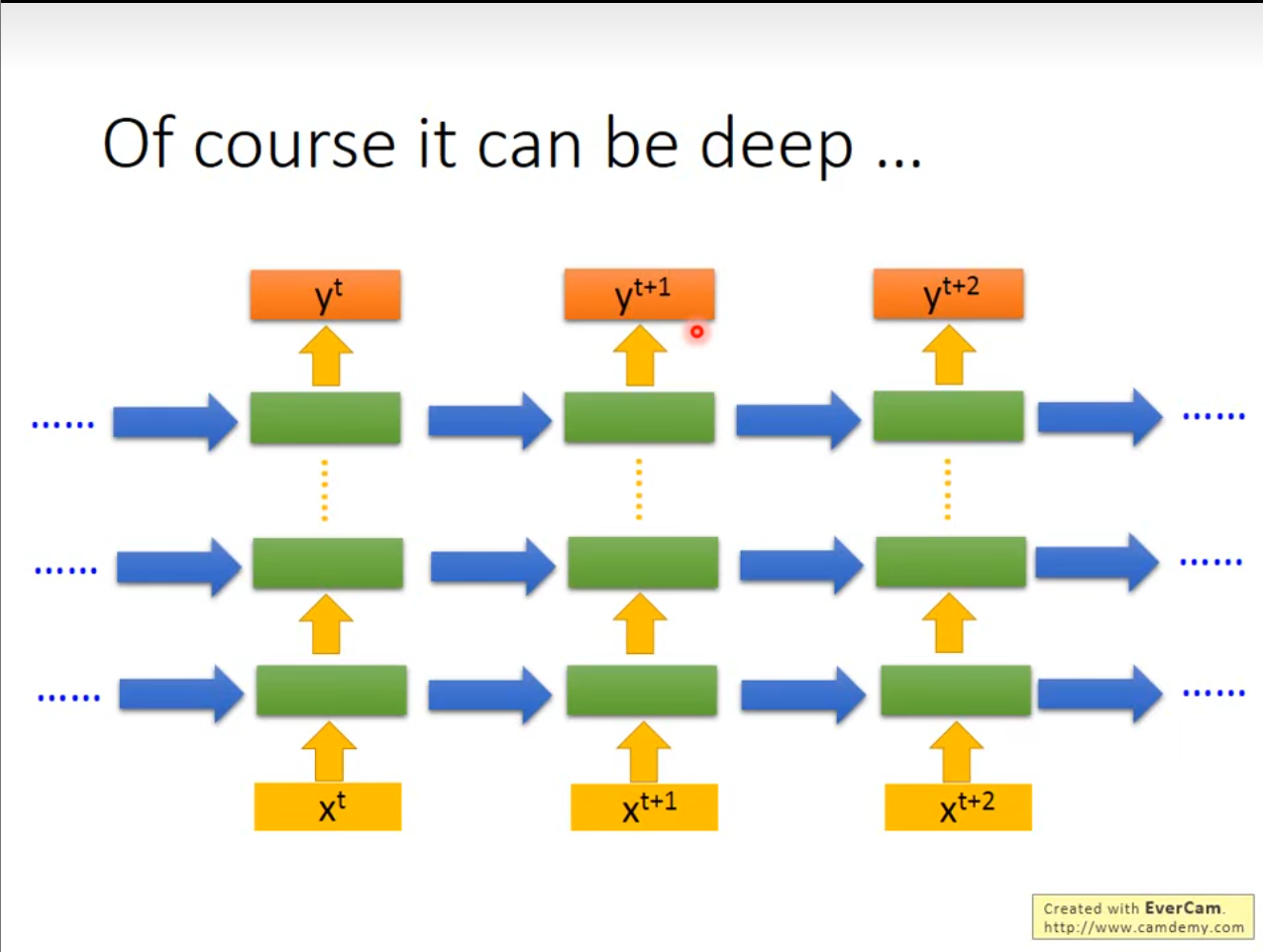
需要注意的是，输入的顺序不同，那么得到的结果也会有所不同。

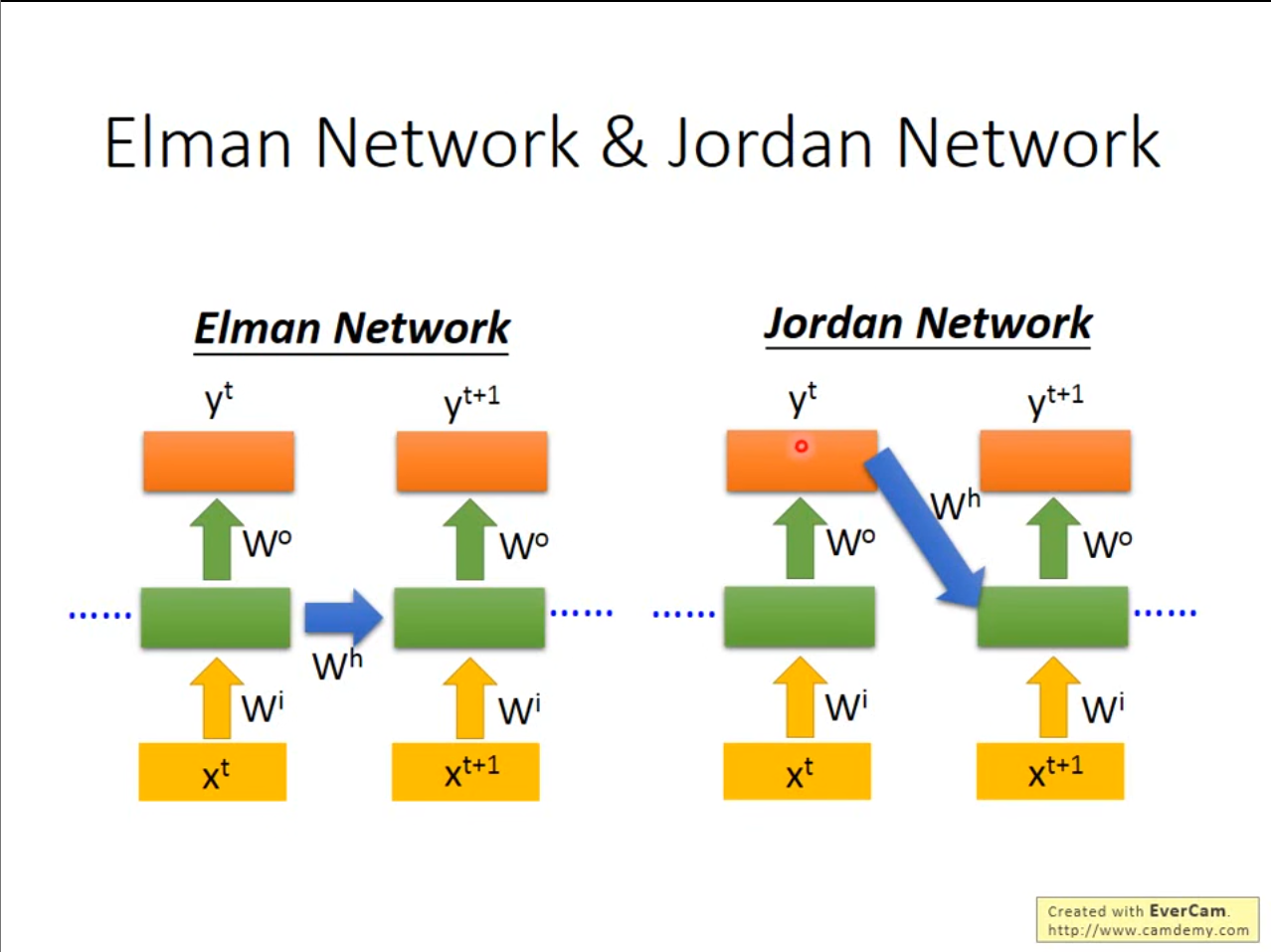
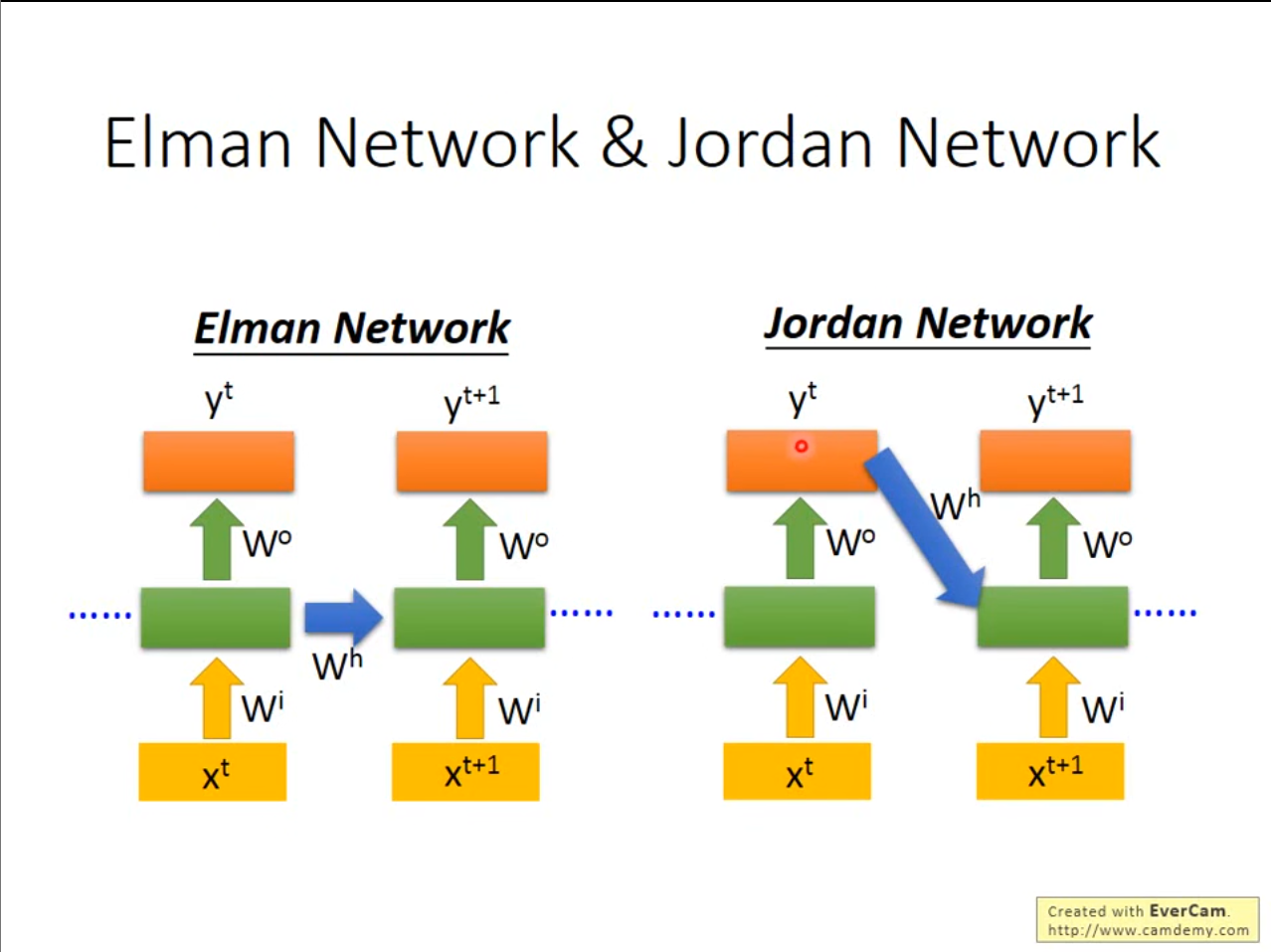
刚才讲的是$ Elman\ Network $，即存储隐藏层的数据，还可以像$ jordan\ Network $一样存储上一次的输出层的结果。

除了刚才的神经网络，还有别的变形，例如上图的双向循环神经网络。

LSTM

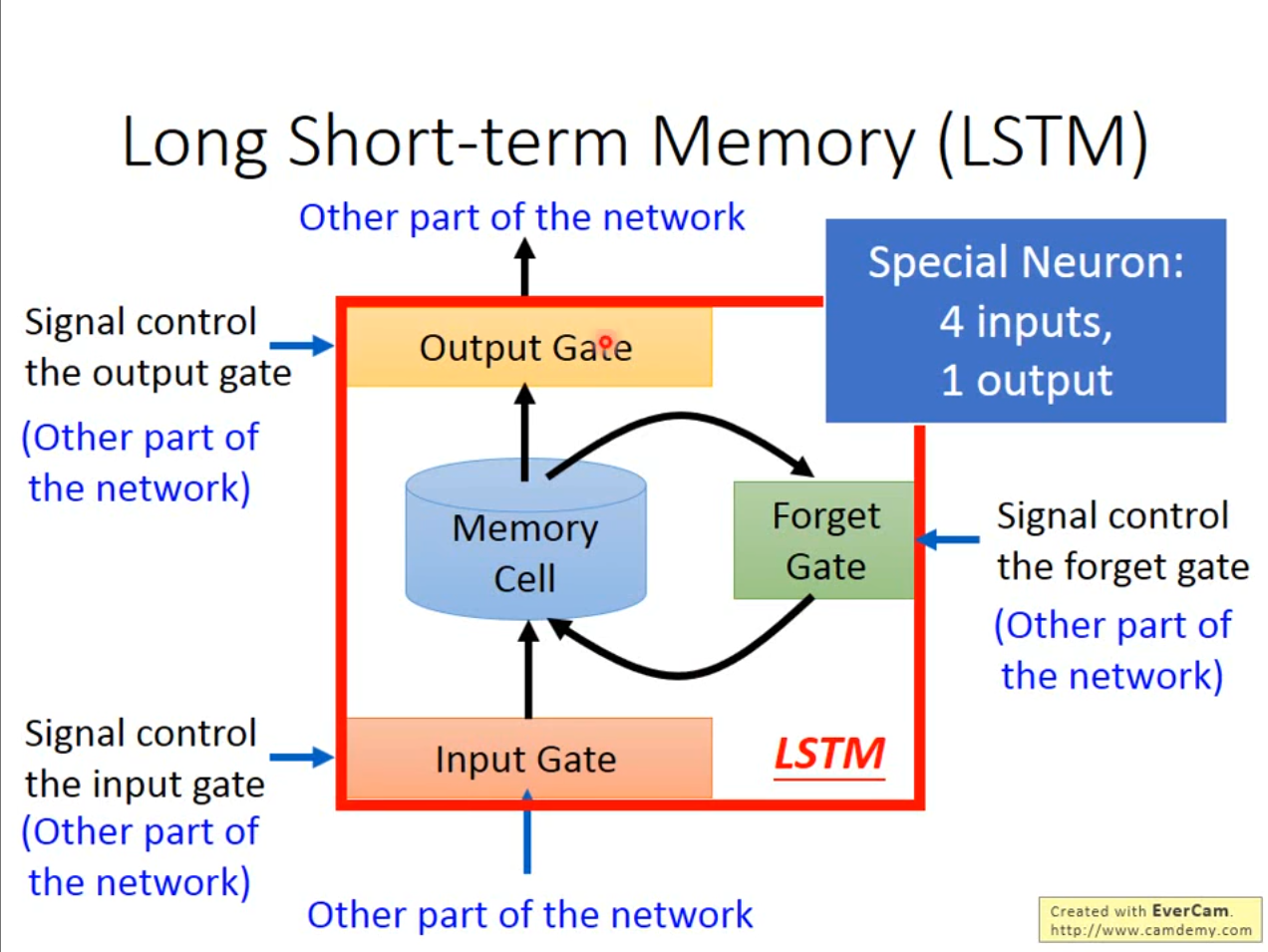
除了像刚刚讲到的最基本的$ RNN $，还可以对它的存储内容进行调整。使用$ Input\ Gate $作为输入控制，判断是否可以讲结果存储$ store $中，使用$ Forget\ Gate $作为判断是否要将存储的数据清空，使用$ Output\ Gate $作为输出控制，判断别的网络是否可以使用这个存储的结果。

有一个冷知识，这个名字长短时记忆网络的断句是长 短时记忆网络，是较长的短时记忆网络，因为比最原始的$ RNN $保留的时间长一些。

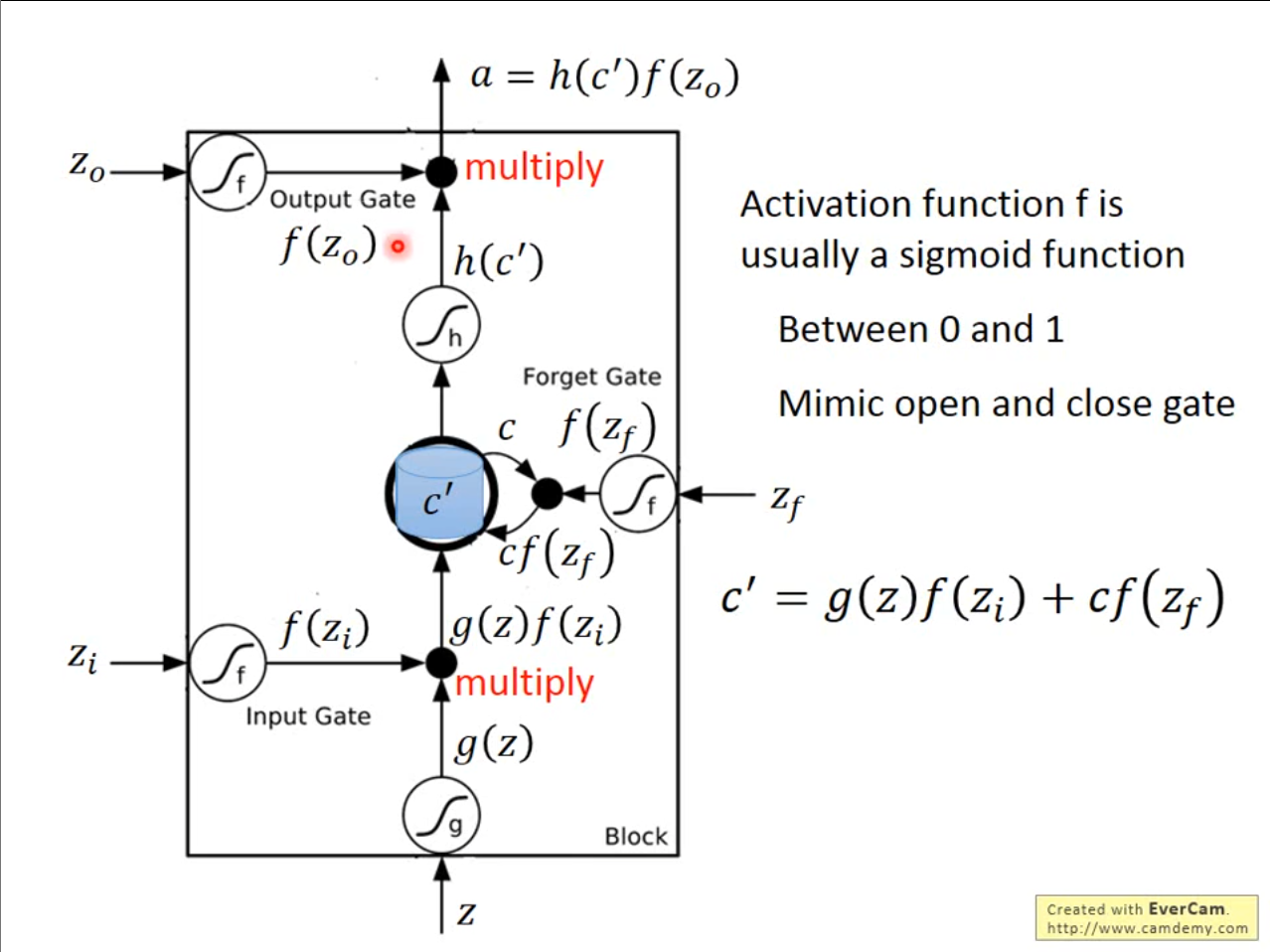
刚才提到的思路如果用数学表达的话就是，$ c’=g(z)f(z_i)+cf\big(z_f\big) $，$ a=h(c^{\prime})f(z_{0}) $。其中$ f $函数作为控制的阀门经常使用$ sigmod $激活函数，因为$ sigmod $的输出是在$ 0,1 $之间也就代表了允许进入多少，输出多少，保留多少。其中$ Forget\ Gata $有一点和名字不同，当$ f(z_f) $的值越大代表保留的越多，和名字的意思有些相反。

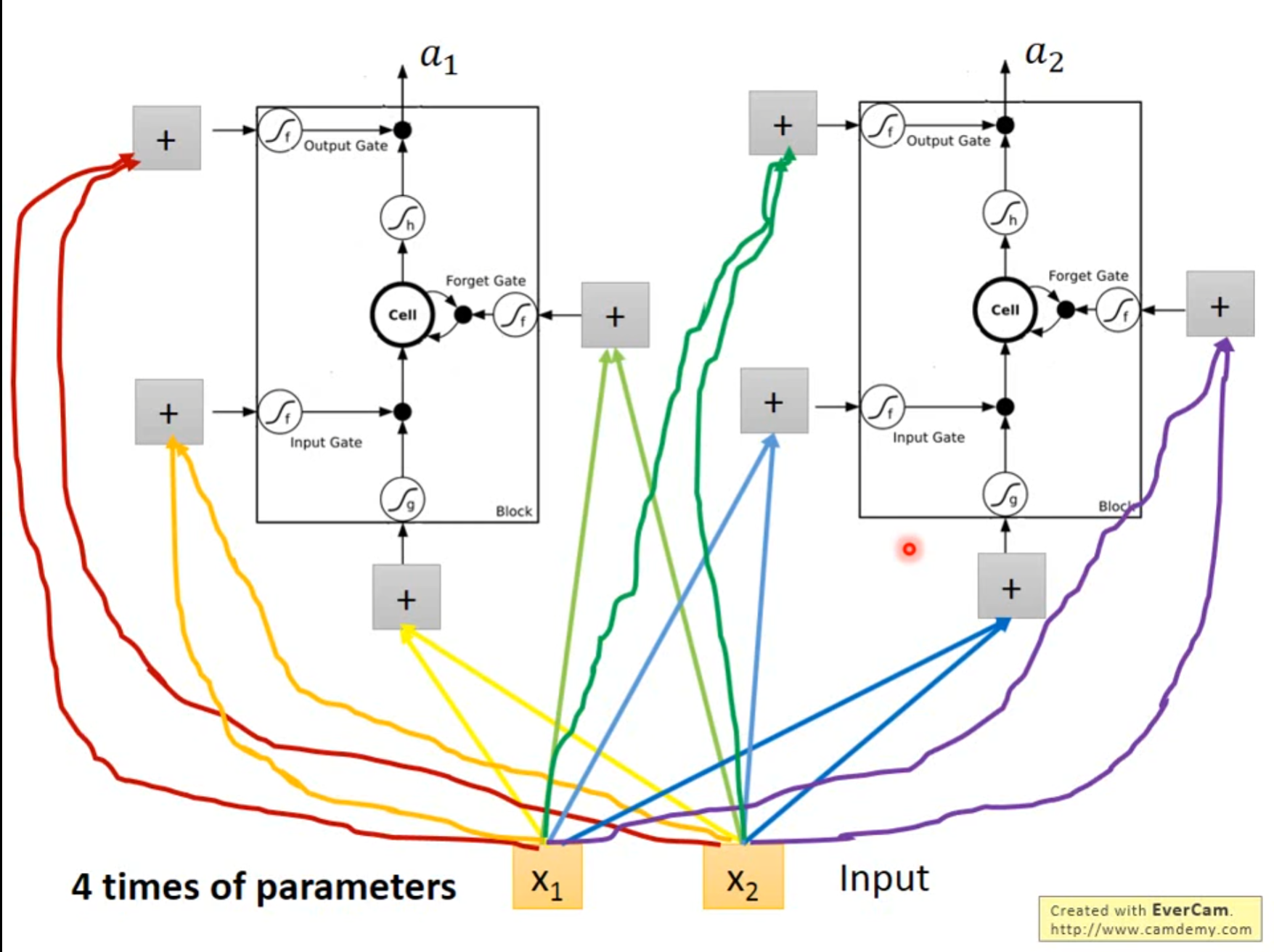
相当于每个神经元都有了四个不同的输入，比之前的输入增加了四倍。

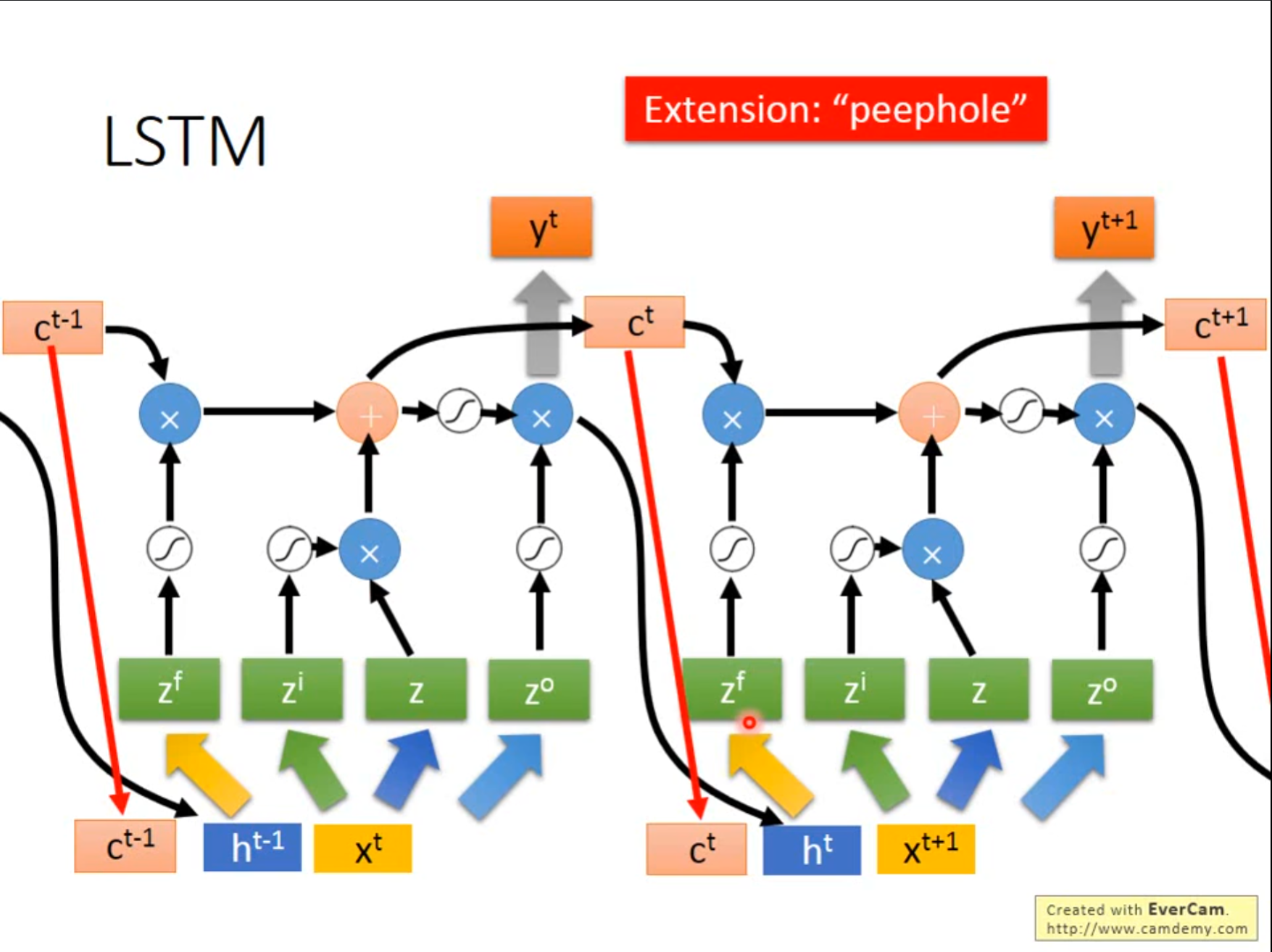
之前讲述的$ LSTM $还不是真正的$ LSTM $，实际上的应该将上次的存储值和隐藏层输出都作为这次的输入考虑进来。

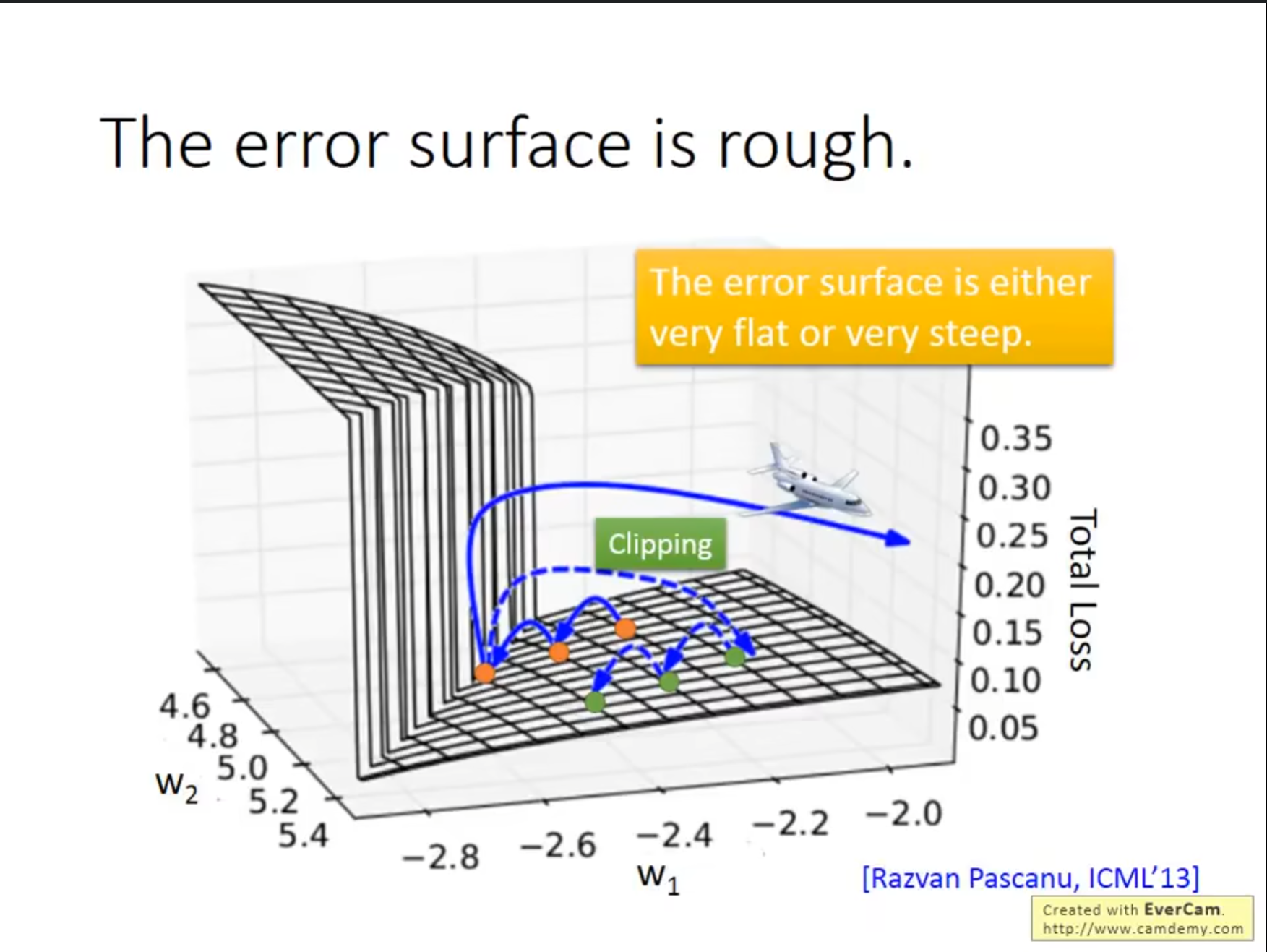
在$ RNN $中还有一个需要注意的问题就是它的梯度可能会变化的非常剧烈，如果此时的梯度较大，但是我们的学习率也比较大，很可能出现$ loss $快速增大的情况，对于这种情况可以选择在梯度达到一定值的时候将其固定。

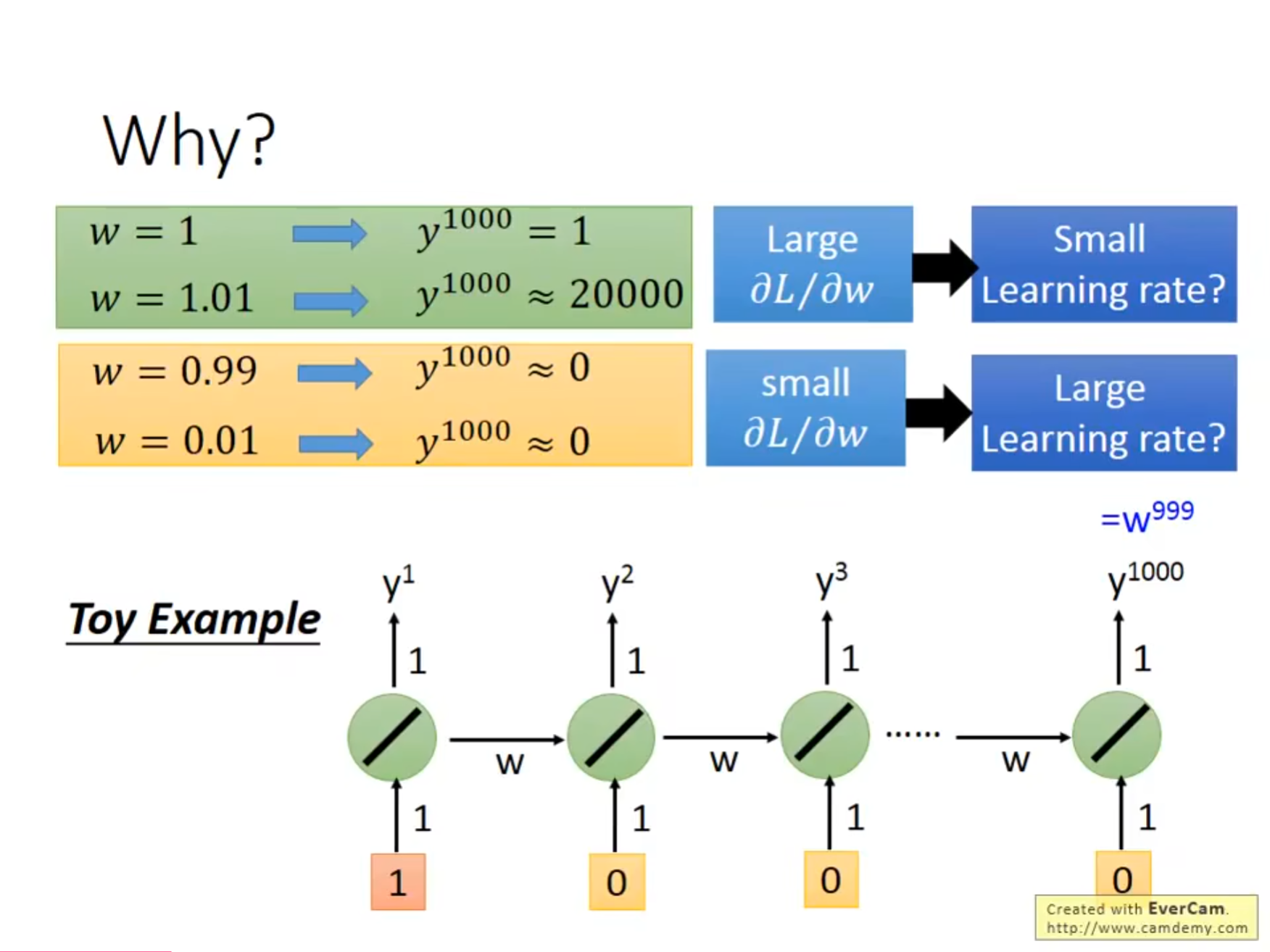
之所以会出现这种情况是因为随着迭代相同的操作可能会执行很多次，有的时候参数的改变起不到影响，但有的时候又会造成很大的改变。

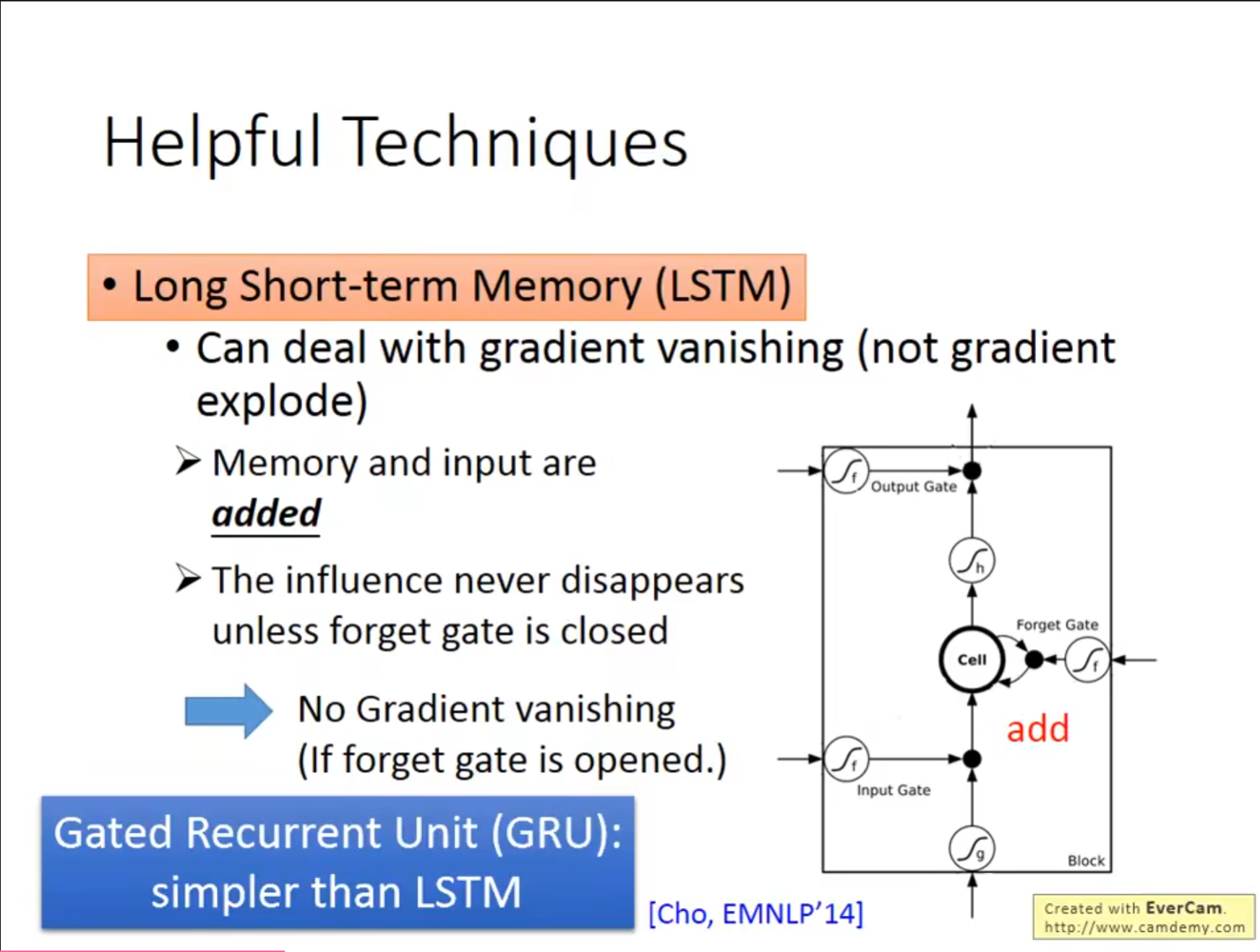
而$ LSTM $可以解决一部分的问题，也就是避免梯度消失，但无法避免梯度爆炸，这样可以将学习率设置的小一些。之所以可以是因为$ LSTM $中始终保存了之前的结果，之前的过程对现在始终有影响，甚至一开始的$ LSTM $是没有$ Forget\ Gate $这个设置的，而通常也将$ Forget\ Gate $的值设置的很大，只有少数的情况会将原来的值重置。