神经网络
引入
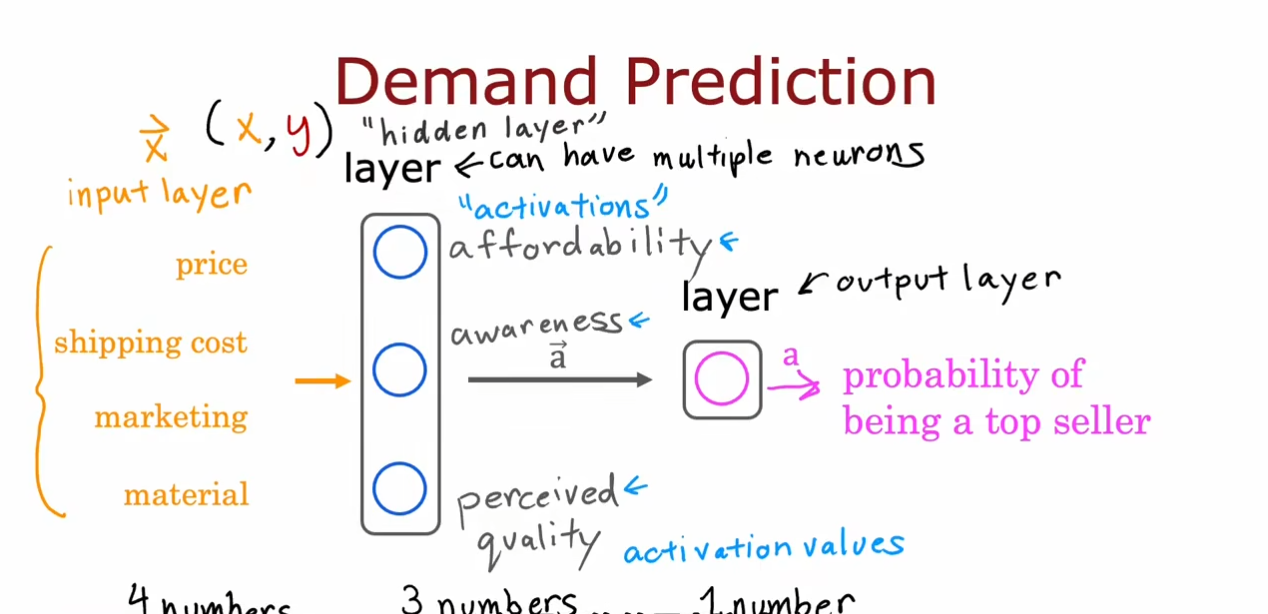
我们使用一个需求预测的例子引入神经网络,再输入层中输入四个特征,接着通过激活函数在隐藏层得到三个激活值。最后将这三个输出作为输出层的输入通过逻辑回归得到一个概率预测。
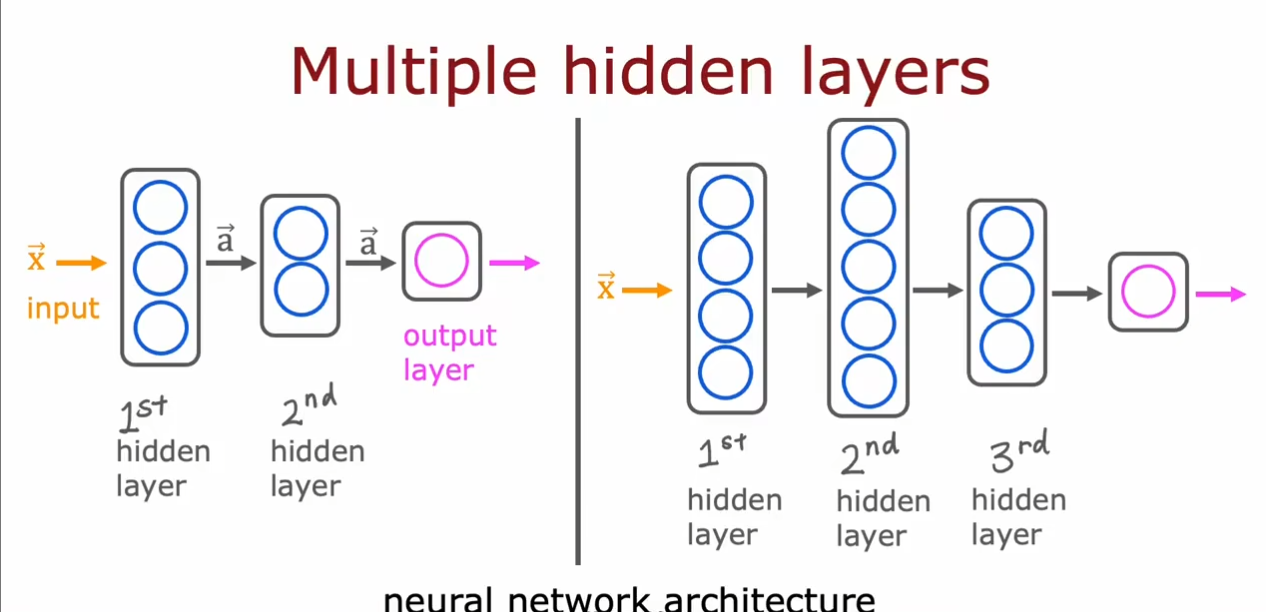
我们可以有多个隐藏层,同时每个隐藏层中的具体特征选择不需要我们自己考虑,但是总共的层数和每层的神经元数量需要我们选择。
图像感知
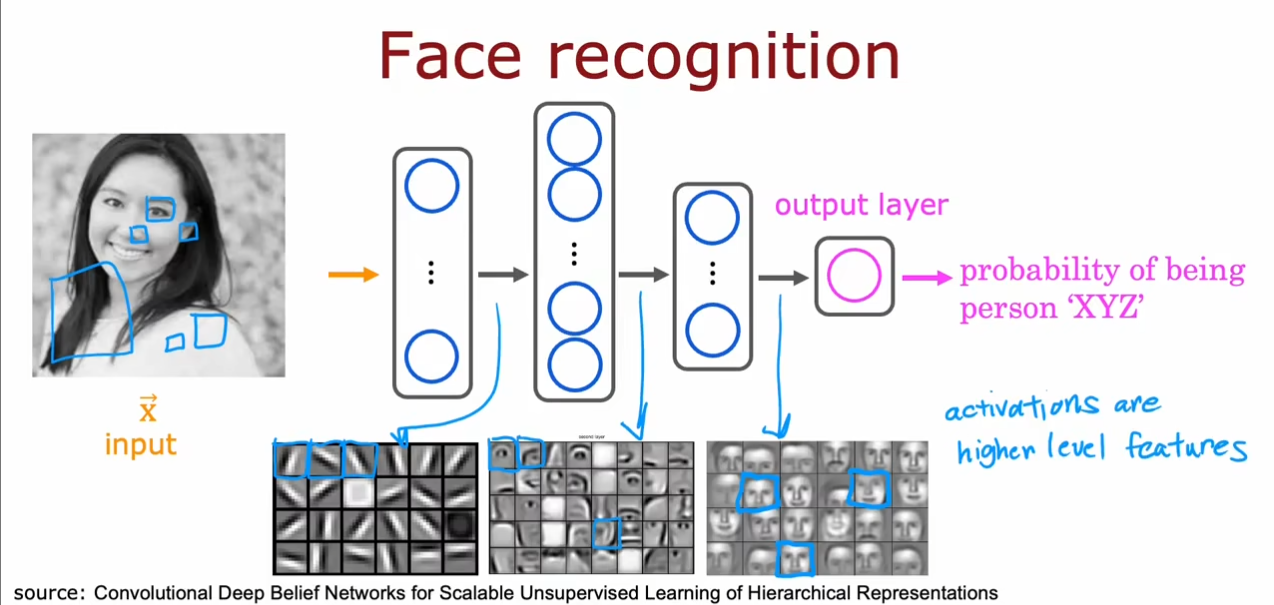
在第一个隐藏层中我们选择一些小的线条,在第二个中选择了眼睛或鼻子等器官,在第三个中选择了整个脸部,最终得到一个预测的可能值。对于这些隐藏层中神经元的内容我们没有指定,而是神经网络根据数据集自己训练的结果。
神经网络中的网络层
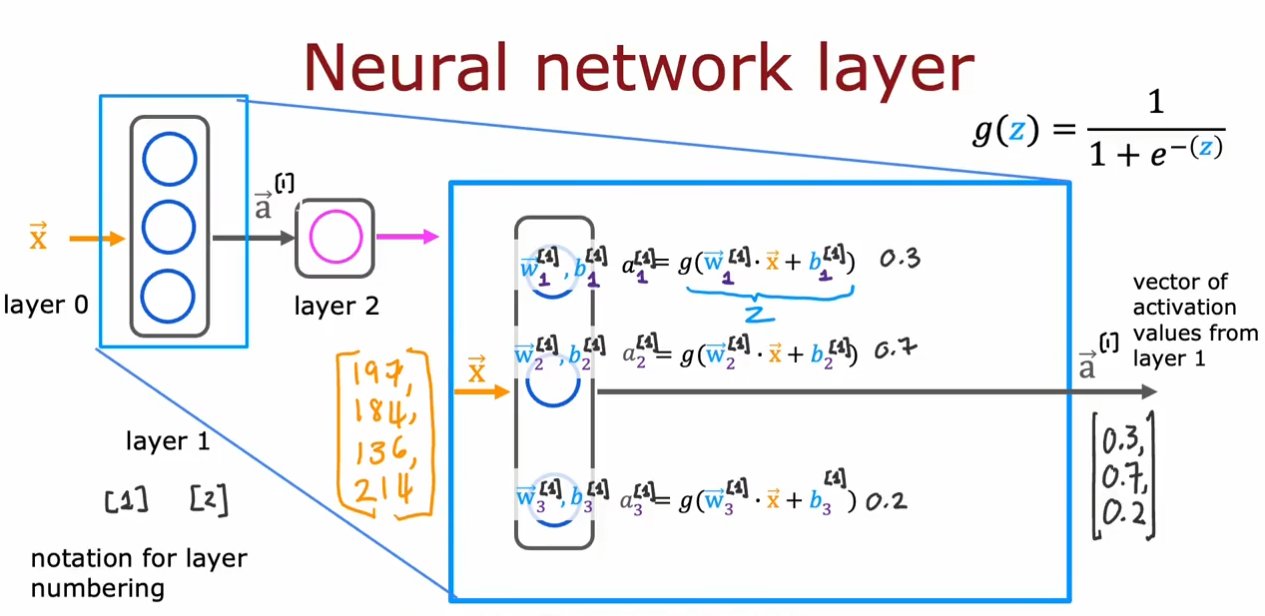
我们将输入层成为第$ 0 $层,接着是第$ 1 $层,第$ 2 $层,第$ n $层,我们放大看第$ 1 $层。
为了区分,我们将上标作为层数标志,例如$ \vec{a}^{[1]} $表示第$ 1 $层的数据。使用下标表示第几个神经元,例如$ \vec{w}_{1}^{[1]} $表示第$ 1 $层中第一个神经元的$ \vec{w} $向量。
我们的输入向量在每个神经元中都进行一个小的逻辑回归运算得到一个概率值$ a $,结合在一起得到了一个输出向量$ \vec{a} $。同时这个向量也可以作为下一层的输入向量。
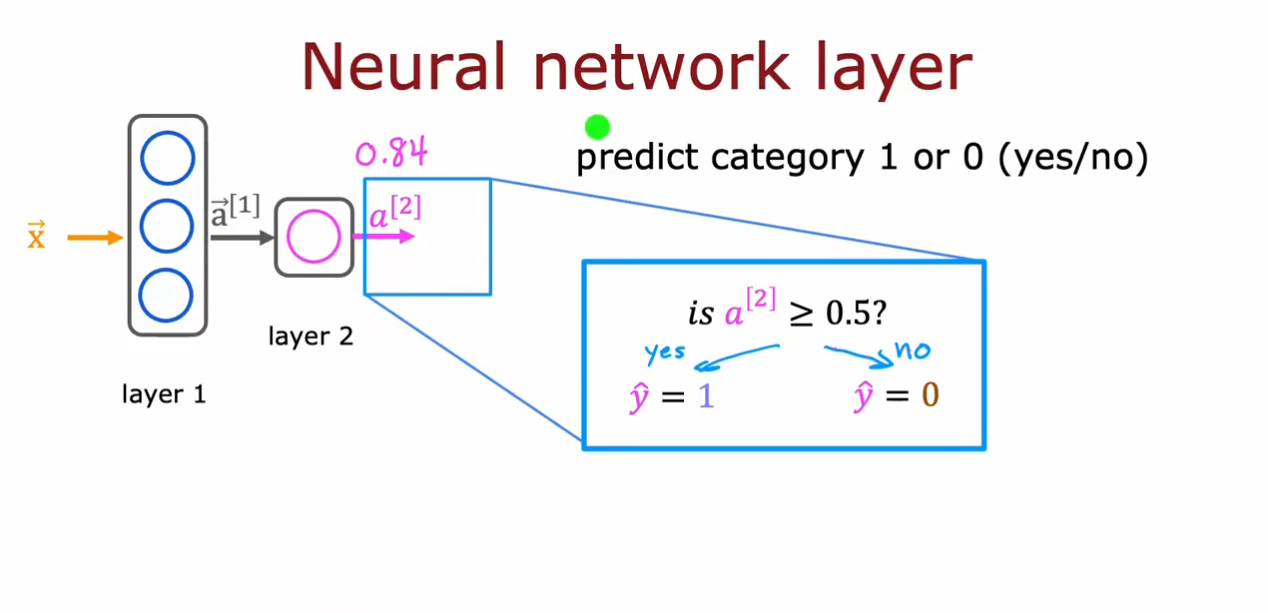
最终我们通过输出层的一个神经元的逻辑回归运算得到一个输出值$ 0.84 $,我们可以设置一个阈值,如果大于这个值就为$ 1 $,否则为$ 0 $。
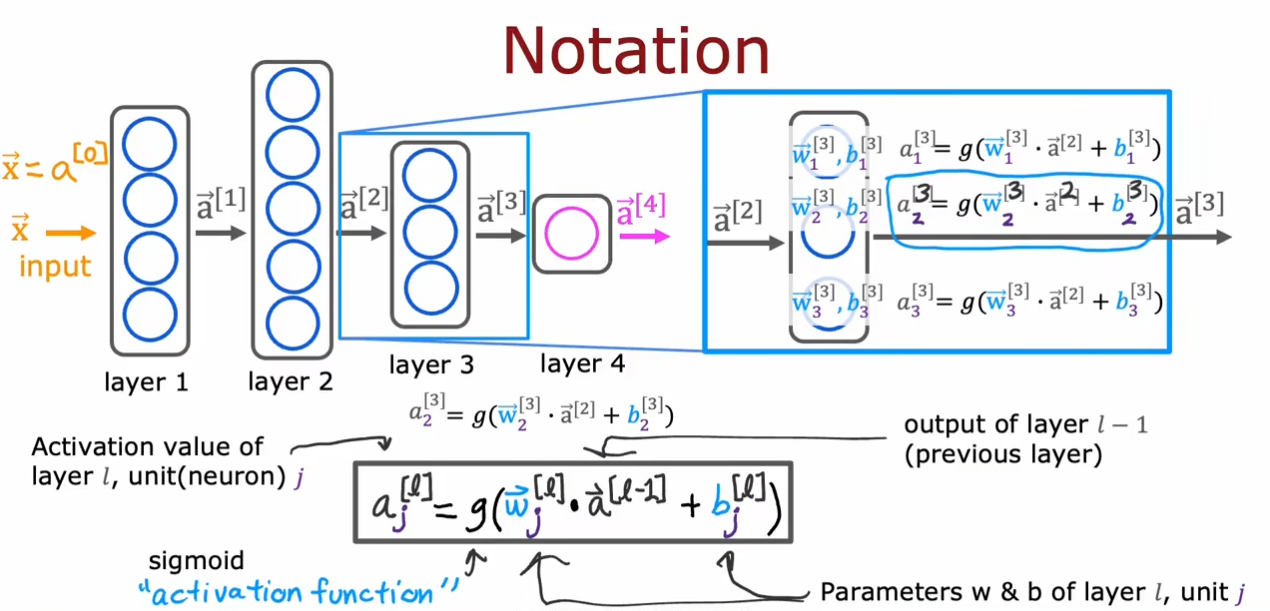
其中$ a $为激活值,$ g $为激活函数$sigmoid$,$ l $为层数,$ j $代表第几个神经元,最后,$ w,b $表示权重和偏置。
前向传播
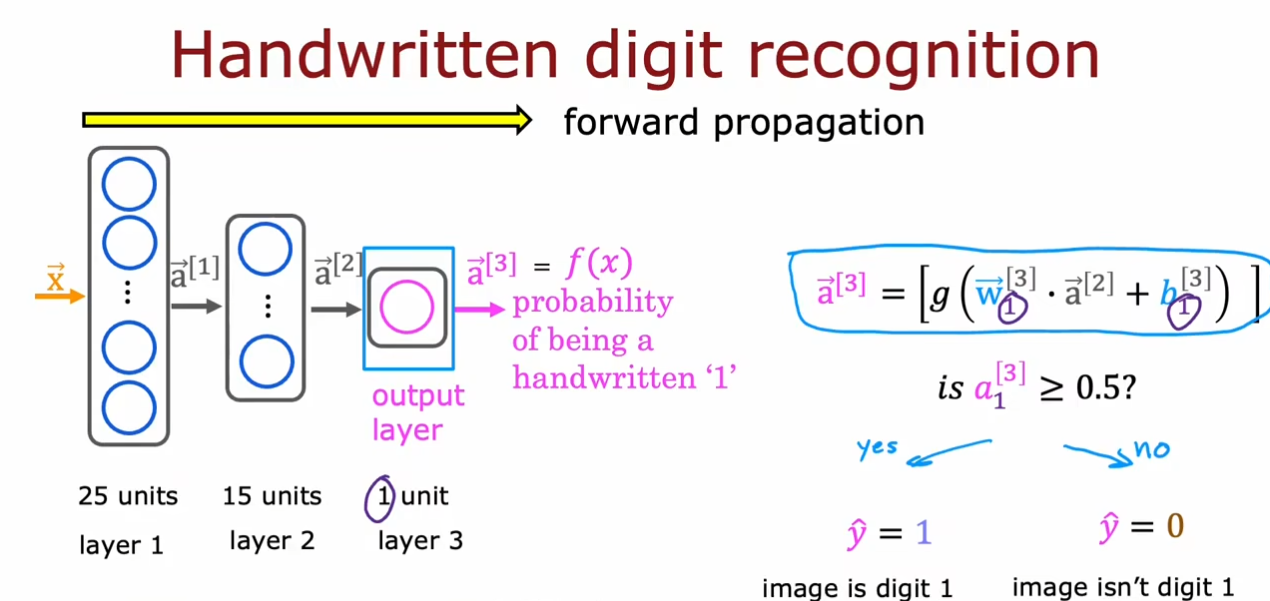
图中从左向右依次计算激活值的过程被称为前向传播。
优化算法
待优化参数$ w $,损失函数$ loss $,学习率$ lr $,每次迭代一个$ batch $,$ t $表示当前$ batch $迭代的总次数:
- 计算$ t $时刻损失函数关于当前参数的梯度$ g_{t}=\nabla loss=\frac{\partial loss}{\partial(w_{t})} $
- 计算$ t $时刻一阶动量$ m_t $和二阶动量$ V_t $
- 计算$ t $时刻下降梯度:$ \eta_t=lr\cdot m_t/\sqrt{V_t} $
- 计算$ t+1 $时刻参数:$ w_{t+1}=w_t-\eta_t=w_t-lr\cdot m_t/\sqrt{V_t} $
一阶动量:与梯度相关的函数
二阶动量:与梯度平方相关的函数
- SGD(随机梯度下降)
$m_t=g_t\quad V_t=1$
$\eta_\mathrm{t}=lr\cdot m_\mathrm{t}/\sqrt{V_t}=lr\cdot g_t$
$w_{t+1}=w_t-\eta_t$
$=w_t-lr\cdot m_t/\sqrt{V_t}=w_t-lr\cdot g_t$
$w_{t+1}=w_t-lr*\frac{\partial loss}{\partial w_t}$
- SGDM(含momentum的SGD),在SGD的基础上增加一阶动量
$ m_t=\beta\cdot m_{t-1}+(1-\beta)\cdot g_t \quad V_t=1 $
$ \begin{aligned}
\eta_{t}=lr\cdot m_{t}/\sqrt{V_{t}}=lr\cdot m_{t} \ =lr\cdot(\beta\cdot m_{t-1}+(1-\beta)\cdot g_{t})
\end{aligned} $
$w_{t+1}=w_\mathrm{t}-\eta_\mathrm{t}$
$=w_\mathrm{t}-lr\cdot(\beta\cdot m_{\mathrm{t-1}}+(1-\beta)\cdot g_\mathrm{t})$
- Adagrad,在SGD的基础上增加二阶动量
$ m_{t}=g_{t}\quad V_{t}=\sum_{\tau=1}^{t}g_{\tau}^{2} $
$\eta_\mathrm{t}=lr\cdot m_t/\left(\sqrt{V_t}\right)$
$=lr\cdot g_t/(\sqrt{\sum_{\tau=1}^tg_\tau^2})$
$w_{t+1}=w_t-\eta_t$
$=w_t-lr\cdot g_t/(\sqrt{\sum_{t=1}^tg_\tau^2})$
- RMSProp,在SGD的基础上增加了二阶动量
$ m_t=g_t\quad V_t=\beta\cdot V_{t-1}+(1-\beta)\cdot g_t^2 $
$\eta_t=lr\cdot m_t/\sqrt{V_t}$
$=lr\cdot g_t/(\sqrt{\beta\cdot V_{t-1}+(1-\beta)\cdot g_t^2})$
$w_{t+1}=w_t-\eta_t$
$=w_t-lr\cdot g_t/(\sqrt{\beta\cdot V_{t-1}+(1-\beta)\cdot g_t^2})$
- Adam,同时结合SGDM一阶动量和RMSProp二阶动量
$m_t=\beta_1\cdot m_{t-1}+(1-\beta_1)\cdot g_t$
修正一阶动量的偏差:$\widehat{m_{t}}=\frac{m_{t}}{1-\beta_{1}^{t}}$
$V_t=\beta_2\cdot V_{step-1}+(1-\beta_2)\cdot g_t^2$
修正二阶动量的偏差:$\widehat{V_{t}}=\frac{V_{t}}{1-{\beta_{2}}^{t}}$
$\eta_t=lr\cdot\widehat{m}_t/\sqrt{\widehat{V}_t}$
$=lr\cdot\frac{m_t}{1-\beta_1^t}/\sqrt{\frac{V_t}{1-\beta_2^t}}$
$w_{t+1}=w_t-\eta_t$
$=w_t-lr\cdot\frac{m_t}{1-{\beta_1}^t}/\sqrt{\frac{V_t}{1-{\beta_2}^t}}$
激活函数
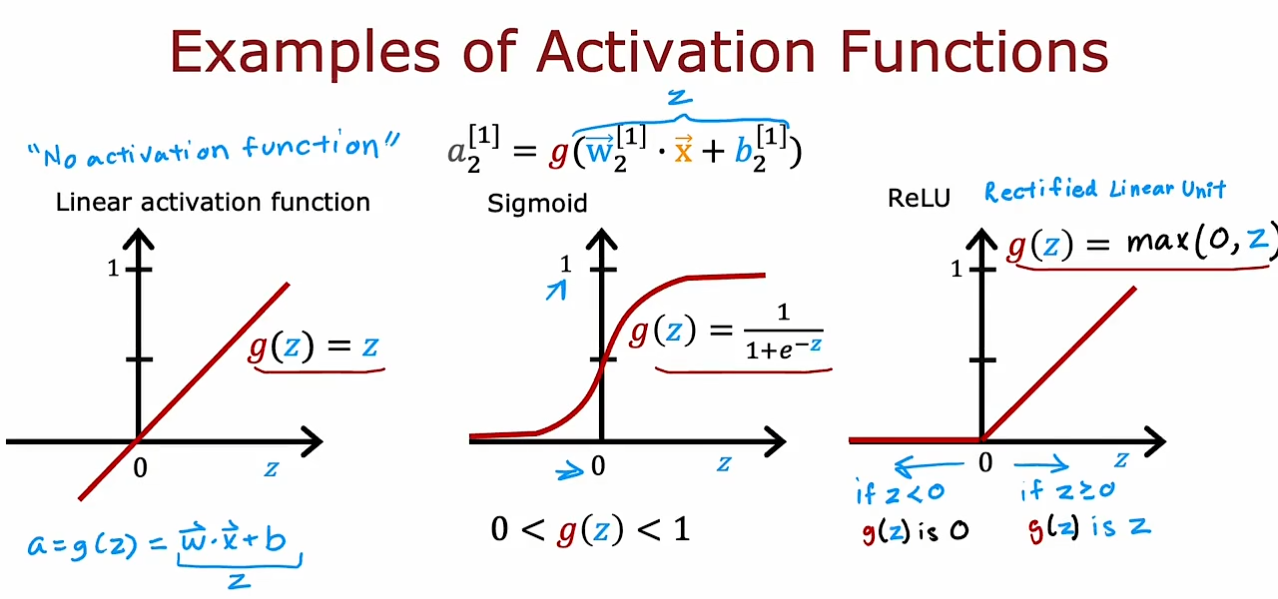
我们可以看到除了我们已经学习过的线性激活函数和$ sigmod $函数,这里还有一种新的激活函数-$ ReLU $函数,也就是$ g(z)=max(0,z) $,适用于输出都是非负数的情况。
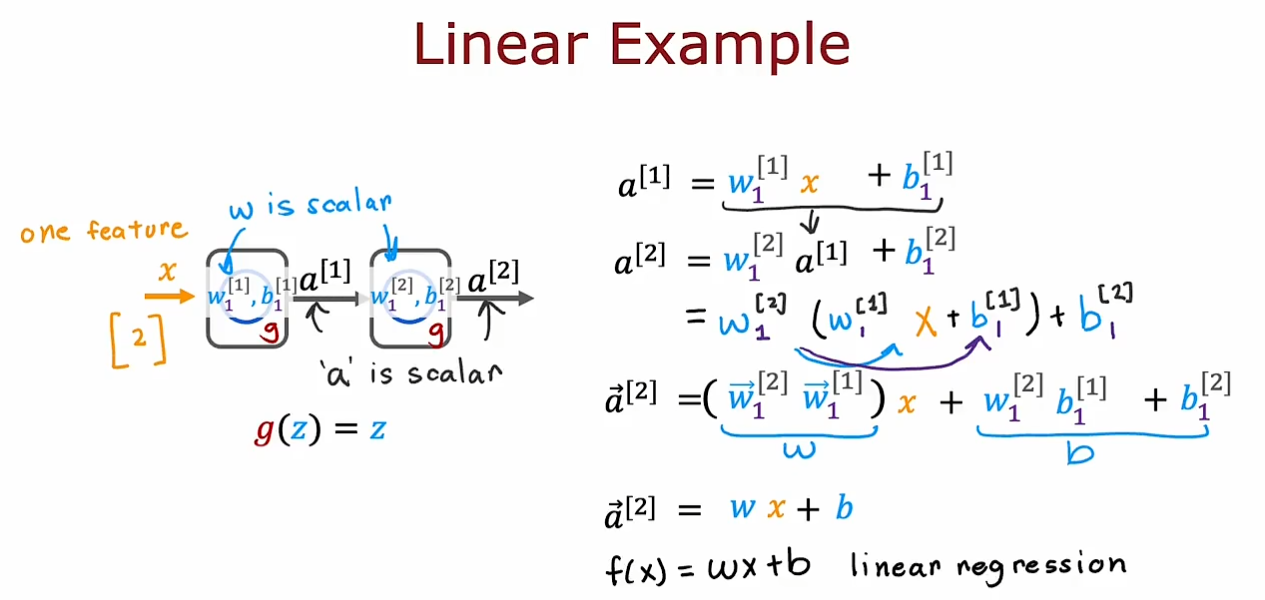
我们现在要学习一下为什么需要非线性的激活函数,如果我们仅仅只是使用线性的激活函数,那么无论我们的隐藏层中有多少的神经元我们也无法拟合一个非线性的目标函数。
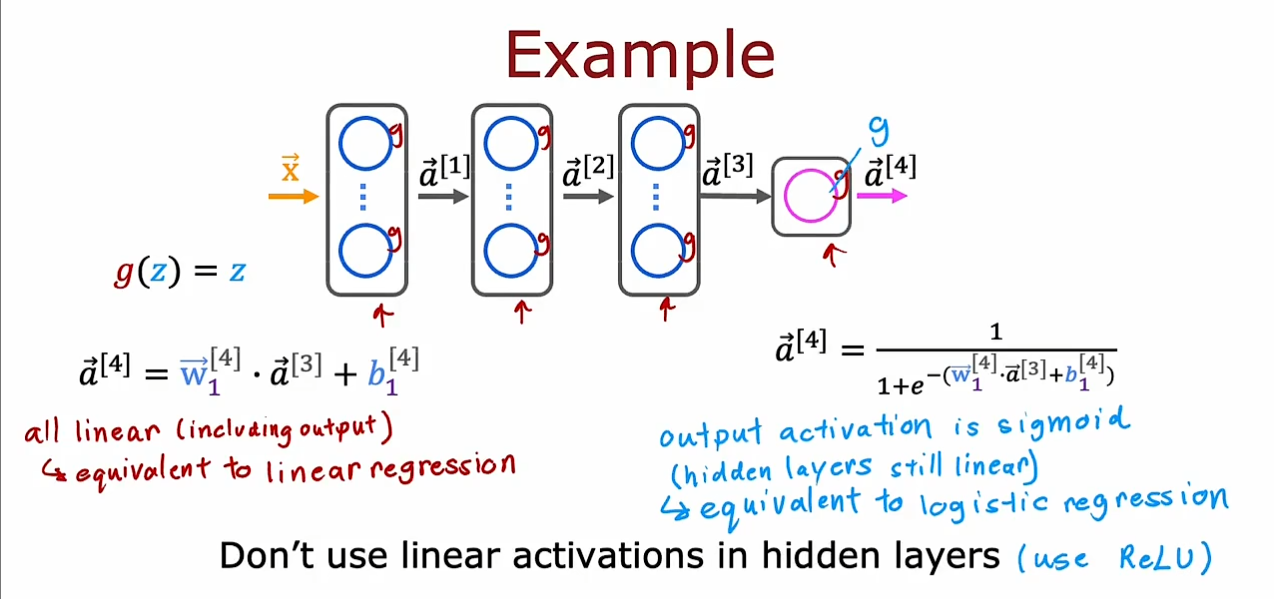
不要在隐藏层中使用线性激活函数,这样的话即使我们在输出层中使用$ sigmod $函数,我们也仅仅是实现了一个逻辑回归函数,因此我们最好是使用$ ReLU $函数。
多分类问题

我们不再仅仅预测一个二分类的问题,而是对多分类问题进行预测,我们使用$ Softmax $函数对线性运算的结果进行处理,使其成为一些列合为$ 1 $的值。其中的$ Softmax $为$ a_{j}=\frac{e^{z_{j}}}{\sum_{k=1}^{N}e^{z_{k}}}=\mathrm{P(y=j|\vec{x})} $
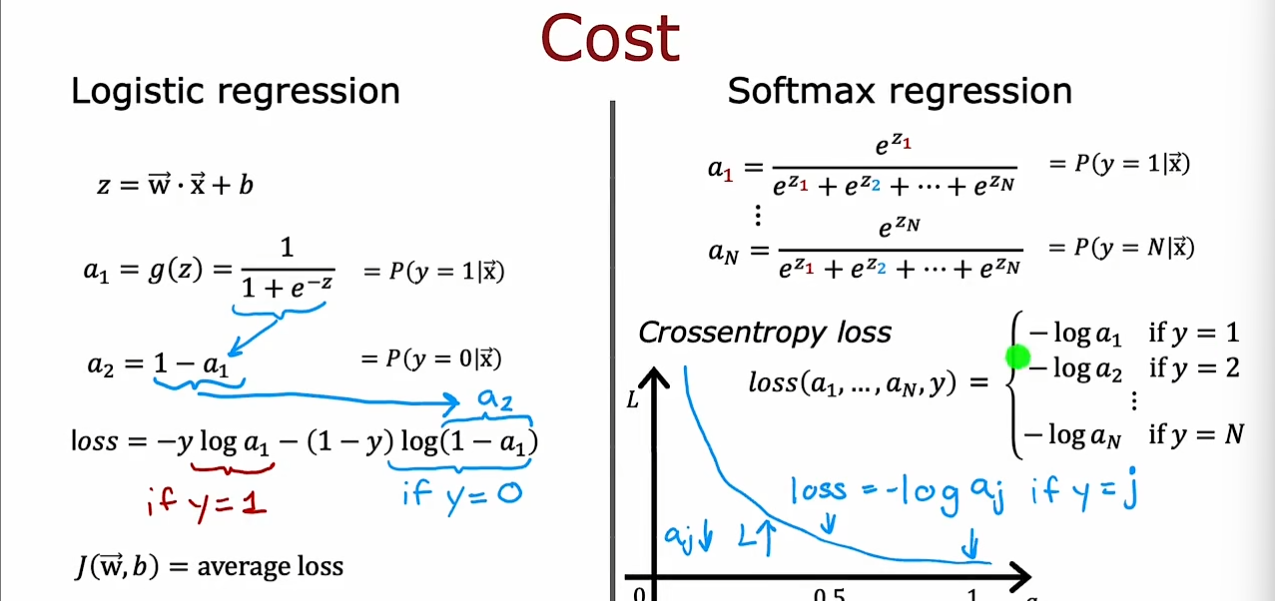
类比$ sigmod $的损失函数,我们可以得到$ Softmax $函数的损失函数为$ loss=-log{a_j} \quad if ~ y=j $

由于$ Softmax $函数中出现了上溢和下溢的问题,我们需要使用指数归一化或者$ LSE $函数对其进行优化,因此,我们可以使用$\text{from logits=True}$对其进行操作,使得$ Softmax $操作和交叉熵的操作放在一起进行并使用$ LSE $避免溢出问题。
同时由于我们在输出层不再进行$ Softmax $操作,因此我们最后的结果依然是具体的数值而不是概率值,因此需要在最后的结果预测时经过$ Softmax $的计算。
具体分析参照:
关于$ Softmax $函数的由来参照:
softmax函数名字的由来(代数&几何原理)——softmax前世今生系列(2)_softmax的由来-CSDN博客
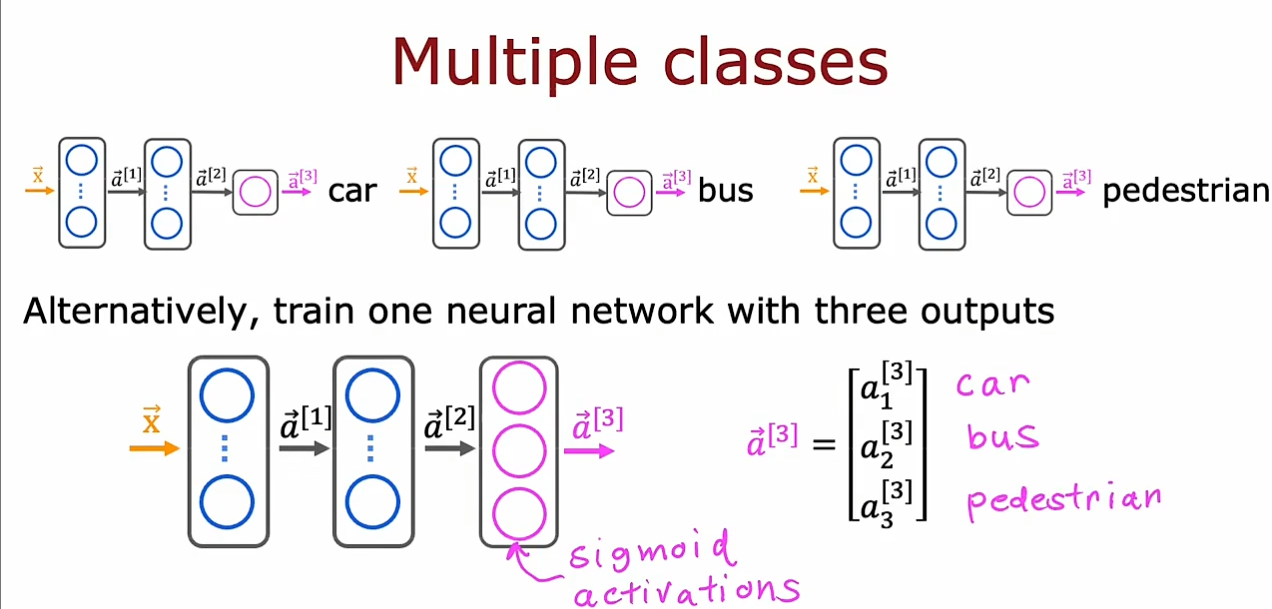
多标签问题和多分类问题不同,多标签问题不具有排他性,可以既是car,又是bus,因此可以使用$ sigmod $激活函数,但是多分类问题时稀疏的,仅可以具有一种性质,采用$ Softmax $。
高级优化方法
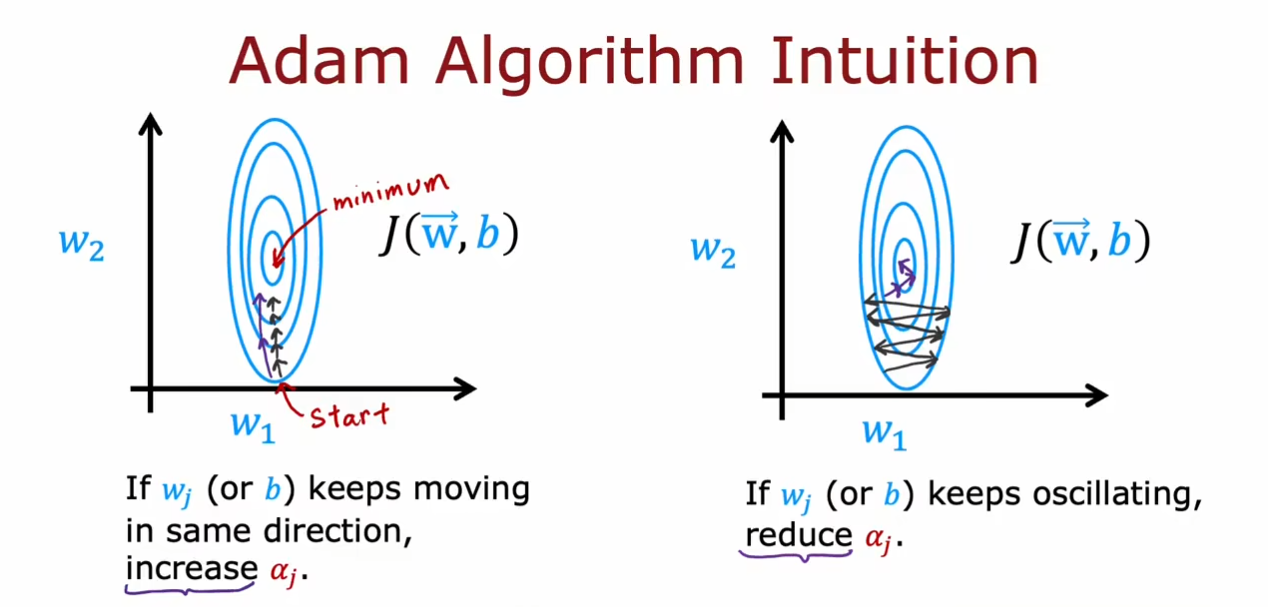
我们可以看到Adam优化器的算法比我们之前的原始梯度下降算法要优秀,可以根据学习率的过大或过小自动调整。
卷积神经网络
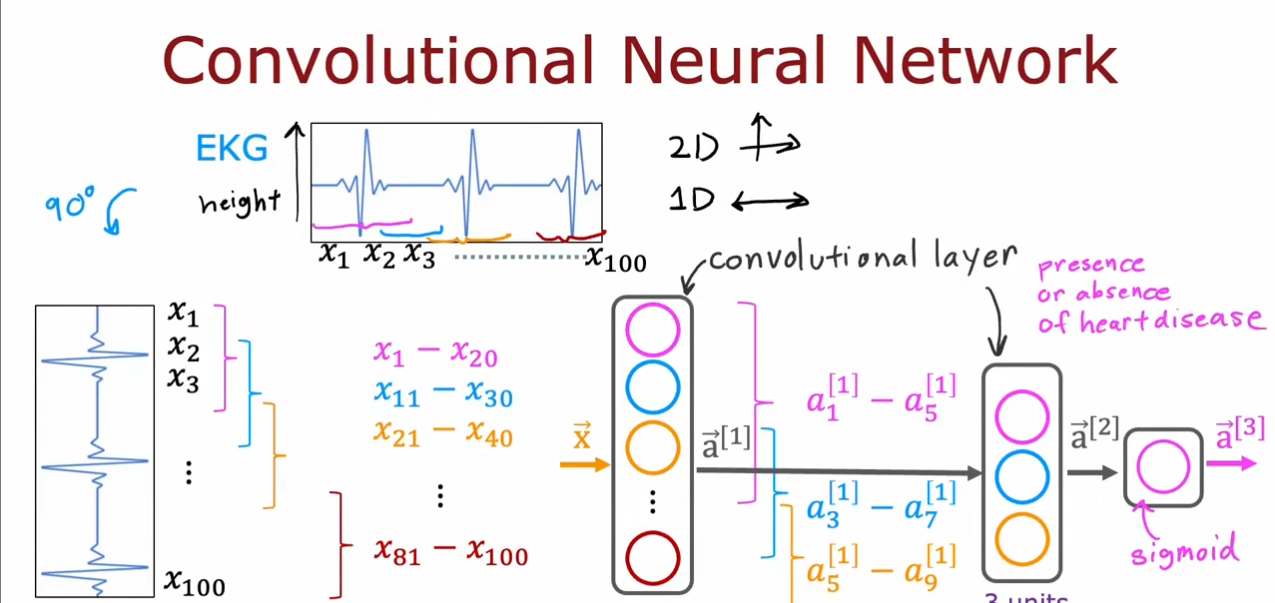
我们可以看到,卷积神经网络和之前学习的全连接网络的区别,我们可以调整每个卷积层的神经元的窗口大小和神经元个数。
计算图

对于自动求导,我们采用了三种方式,分别是符号求导,数值求导和计算图。
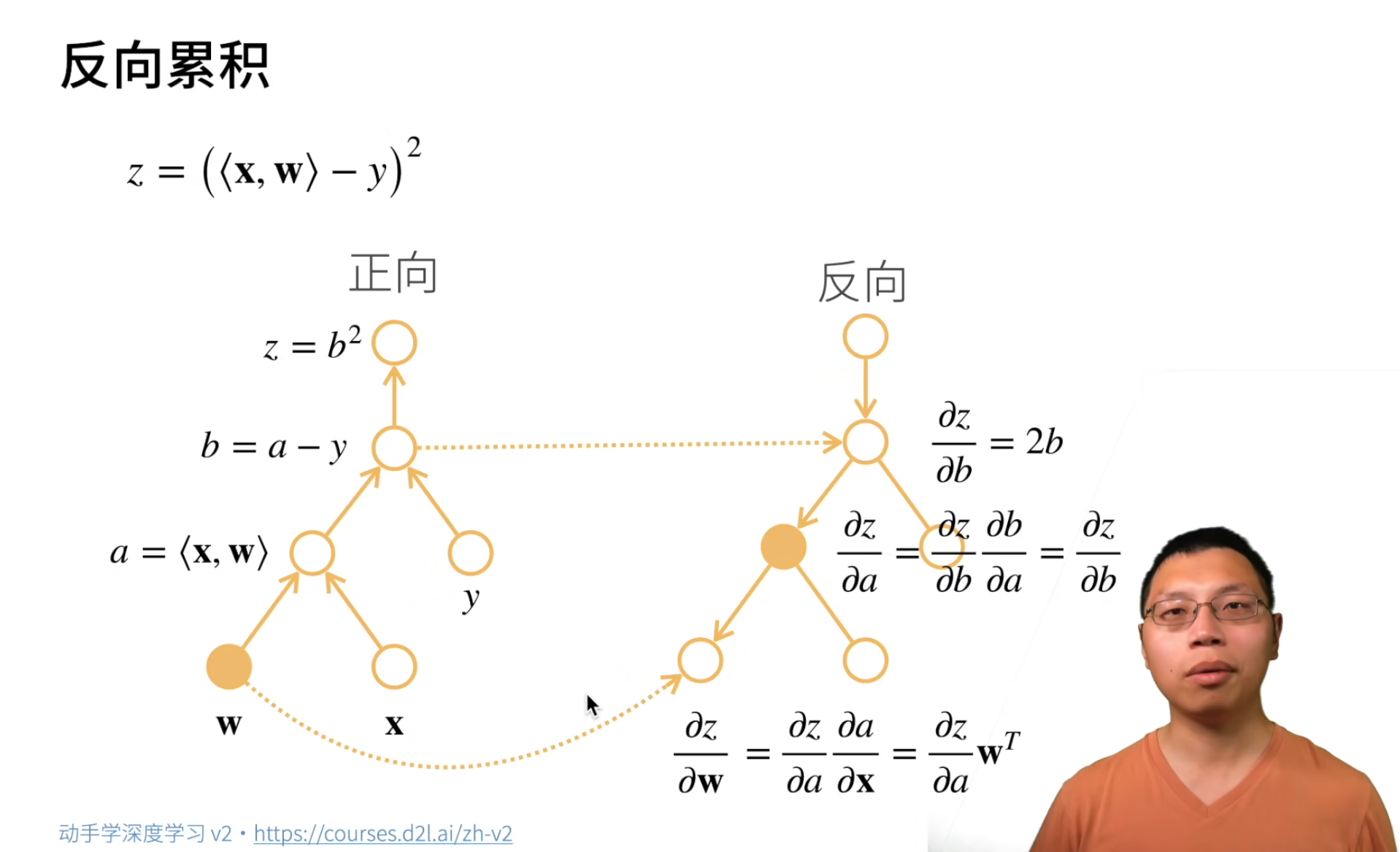
我们在这里采用了计算图的方式来进行自动求导,使用一个有向无环图进行求导。分为两步,分别是前向传播和反向传播。前向传播中我们计算数值,实际上就是为反向传播的求导过程准备数值。如图中,$ \frac{\partial z}{\partial b}=2b $我们就用到了前向传播中的$ b $。

反向累积中我们无论时正向传播还是反向传播,我们需要的计算都是相同的,同时由于需要保存中间变量,需要的内存会是$ O(n) $,但是对于正向累计来讲,由于每次计算一个导数都需要遍历后面的节点,因此它的时间复杂度远远大于反向累积,同时由于它不需要存储中间变量,它的空间复杂度很低。