卷积神经网络
介绍CNN
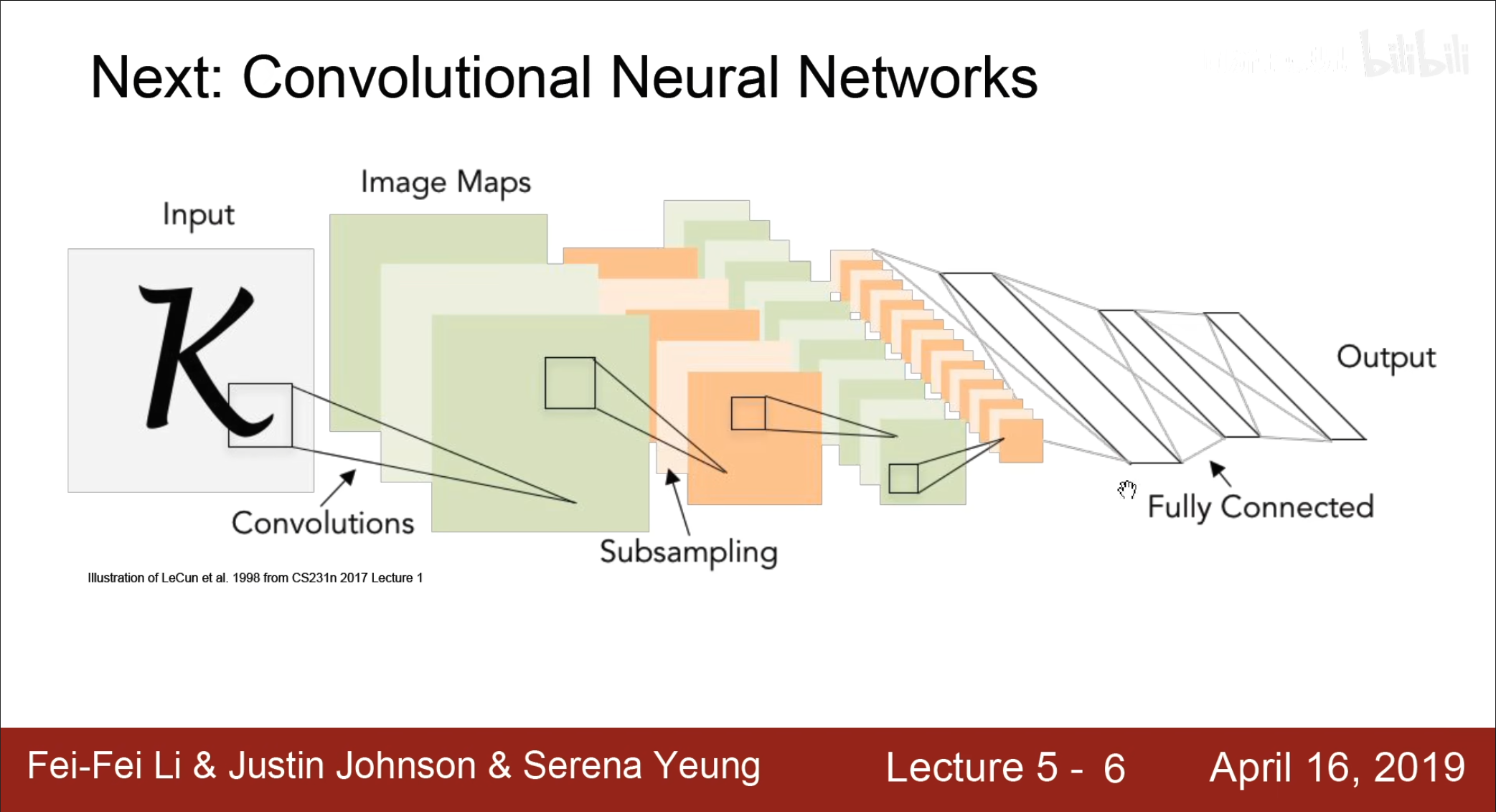
对于卷积神经网络来讲,卷积,下采样,全连接是属于卷积神经网络最重要三个部分,接下来分别进行介绍。
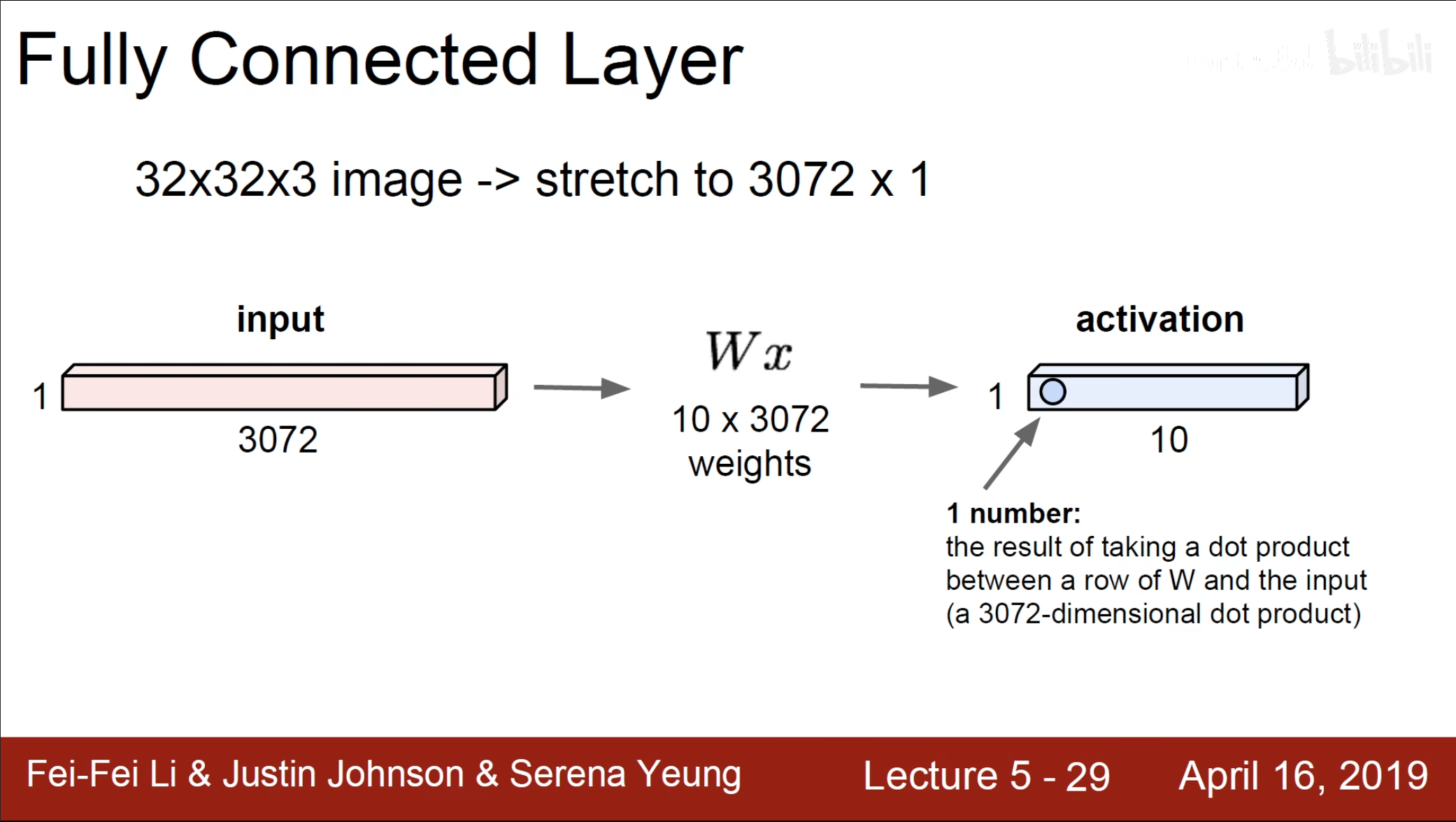
在之前的全连接中,在处理数据之前我们通常将全部的数据拉伸为一个直线,接着进行数据处理,但是这样的话会丢失一些空间信息。
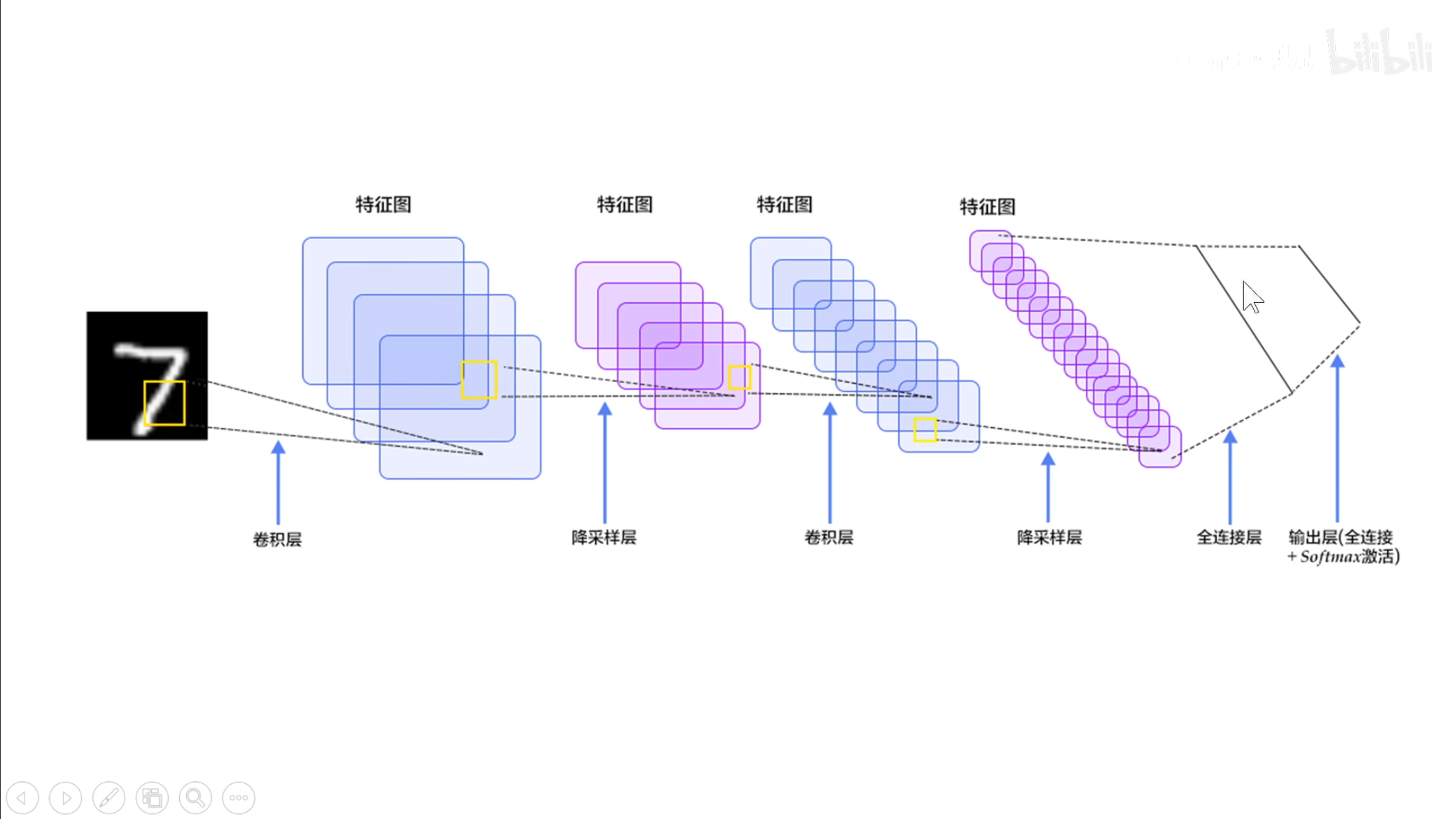
因此,我们就需要使用这个卷积神经网络,每个卷积层跟着一个池化,最终加上全连接和输出层。
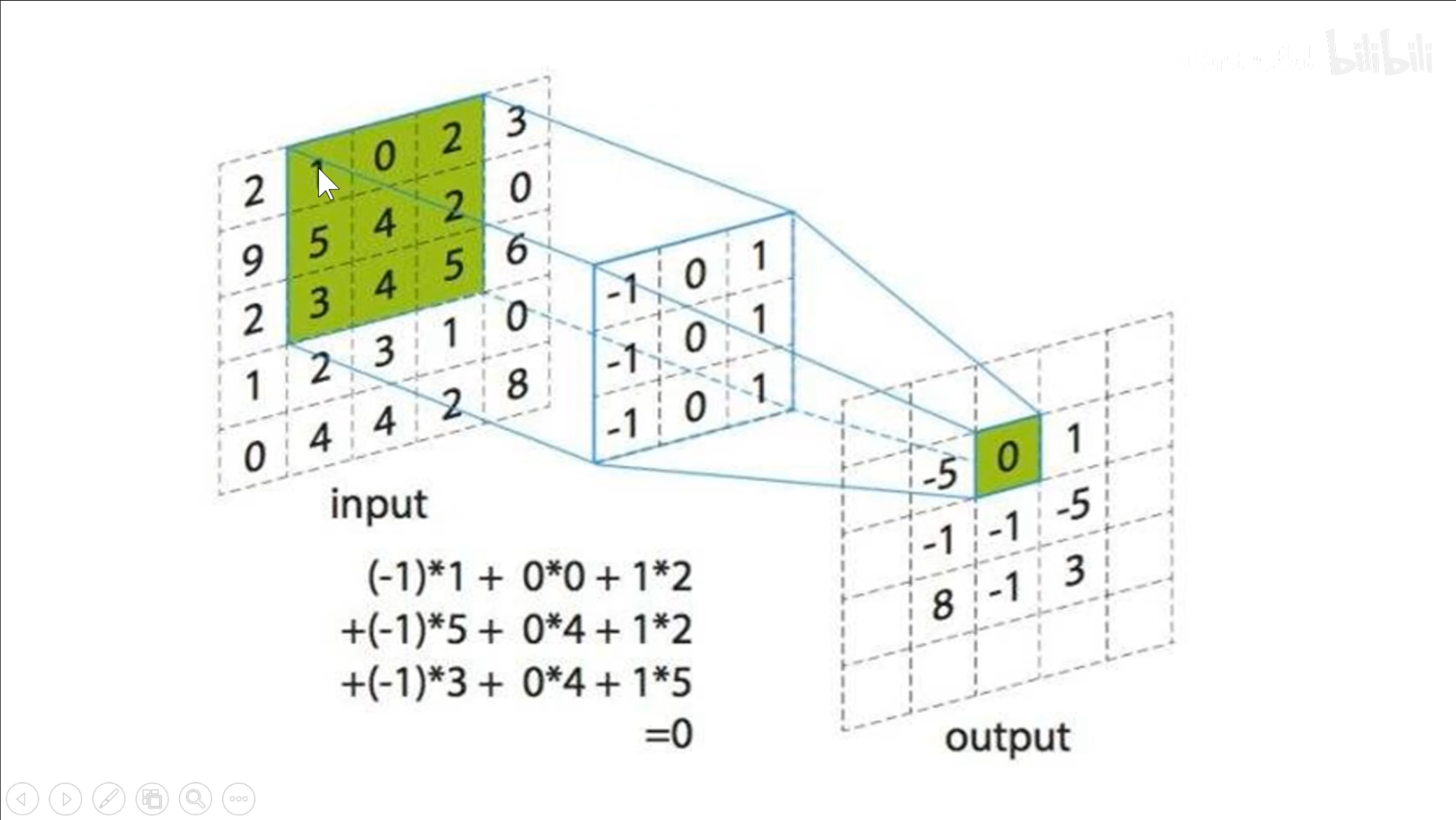
上图就是具体的卷积过程,其中$ input $中的绿色部分就是一个局部感受野,中间的$ 3\times3 $的矩阵就是一个卷积核,将这两个内容两两相乘再相加,最终得到的数据就是输出的值。
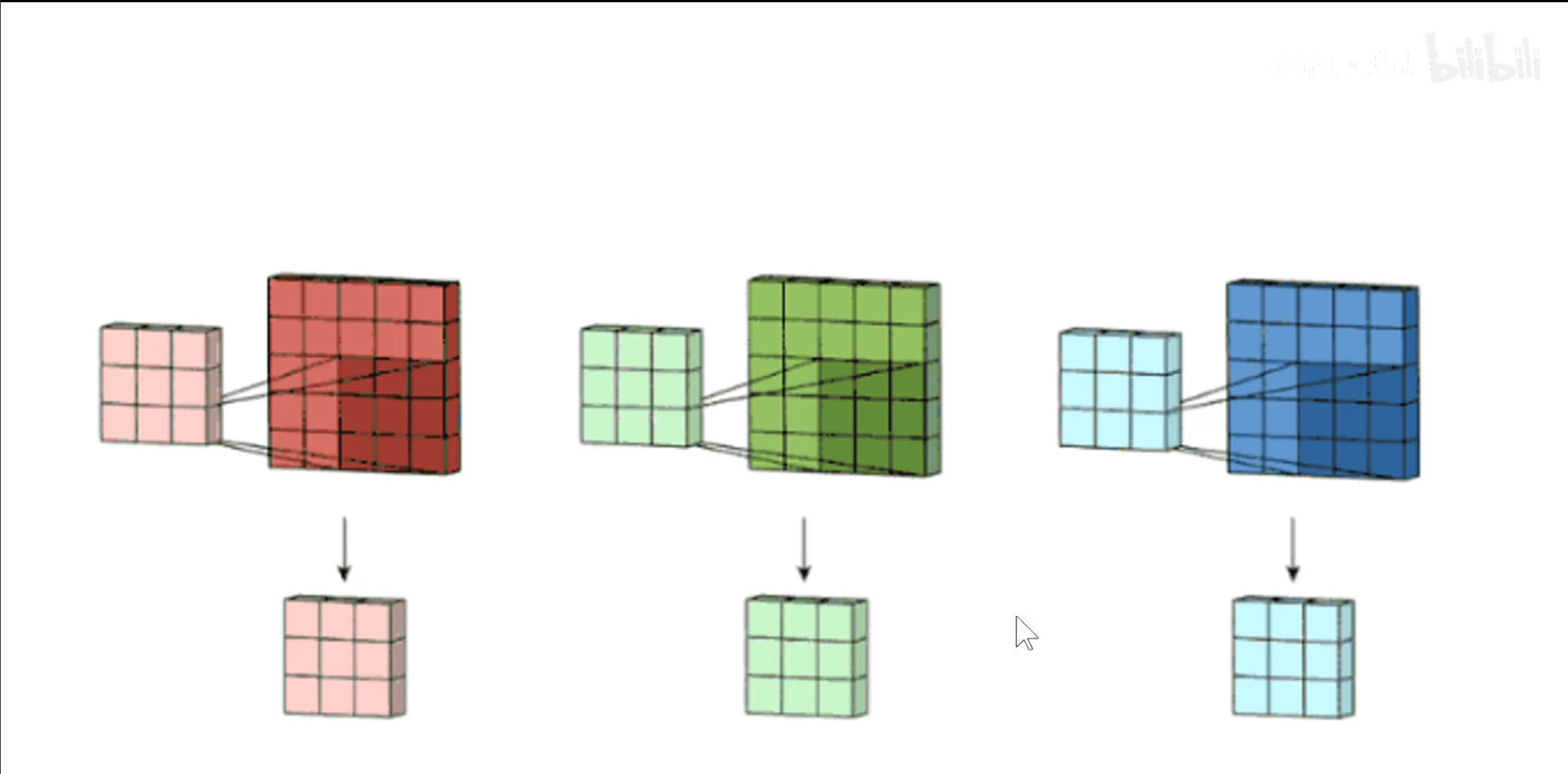
每个卷积核经过计算之后都会得到一个$ feature\ map $(特征图),上图中存在三个卷积核,因此得到三个$ feature\ map $,将这三个$ feature\ map $叠加在一起就是下一层的输入值。
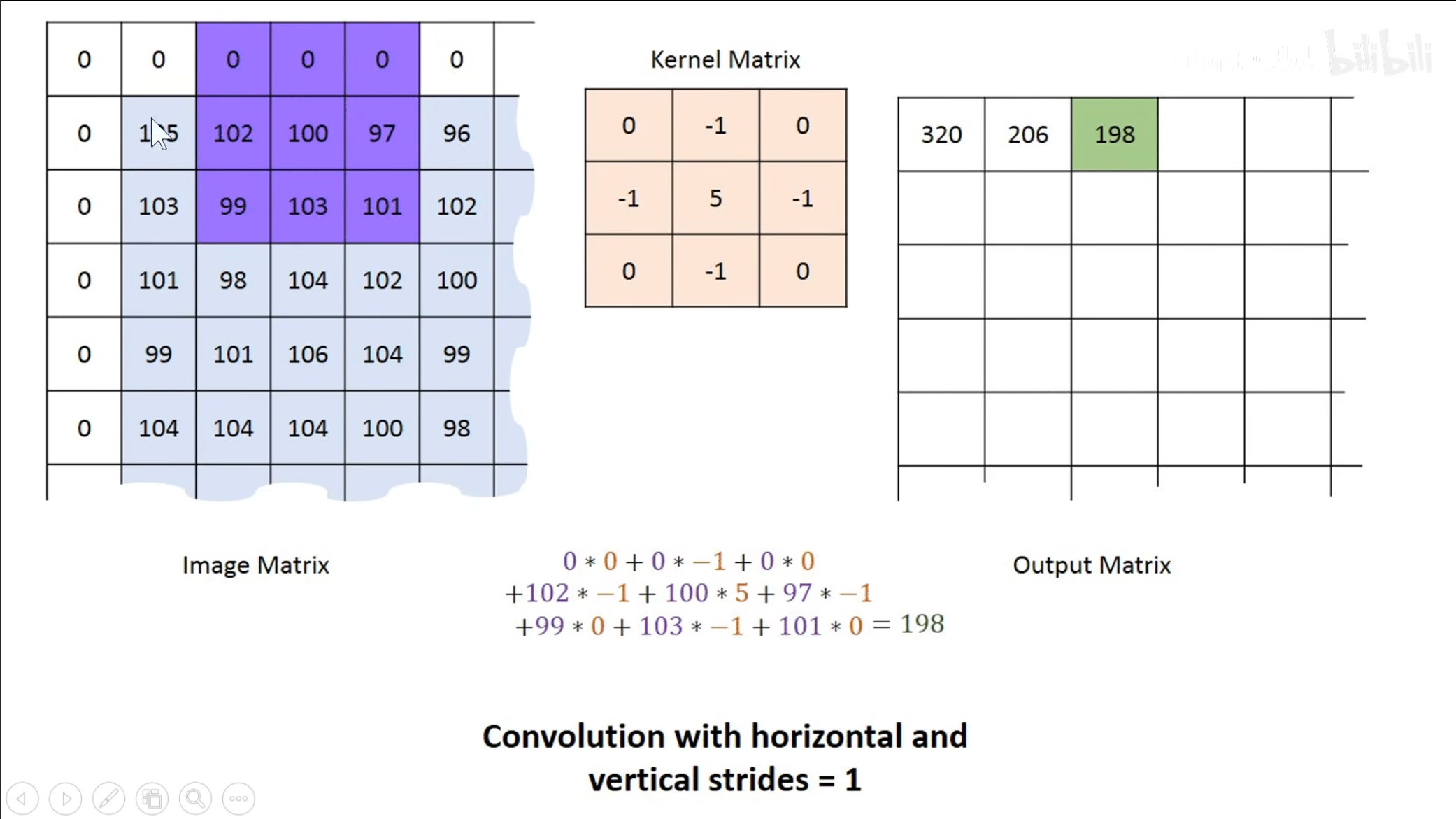
同时需要注意的是,在计算中边缘数据的访问要少于中间数据的访问,因此我们可以通过填充数据$ 0 $来进行优化,这样也可以避免随着卷积计算得到的$ feature\ map $越来越小。
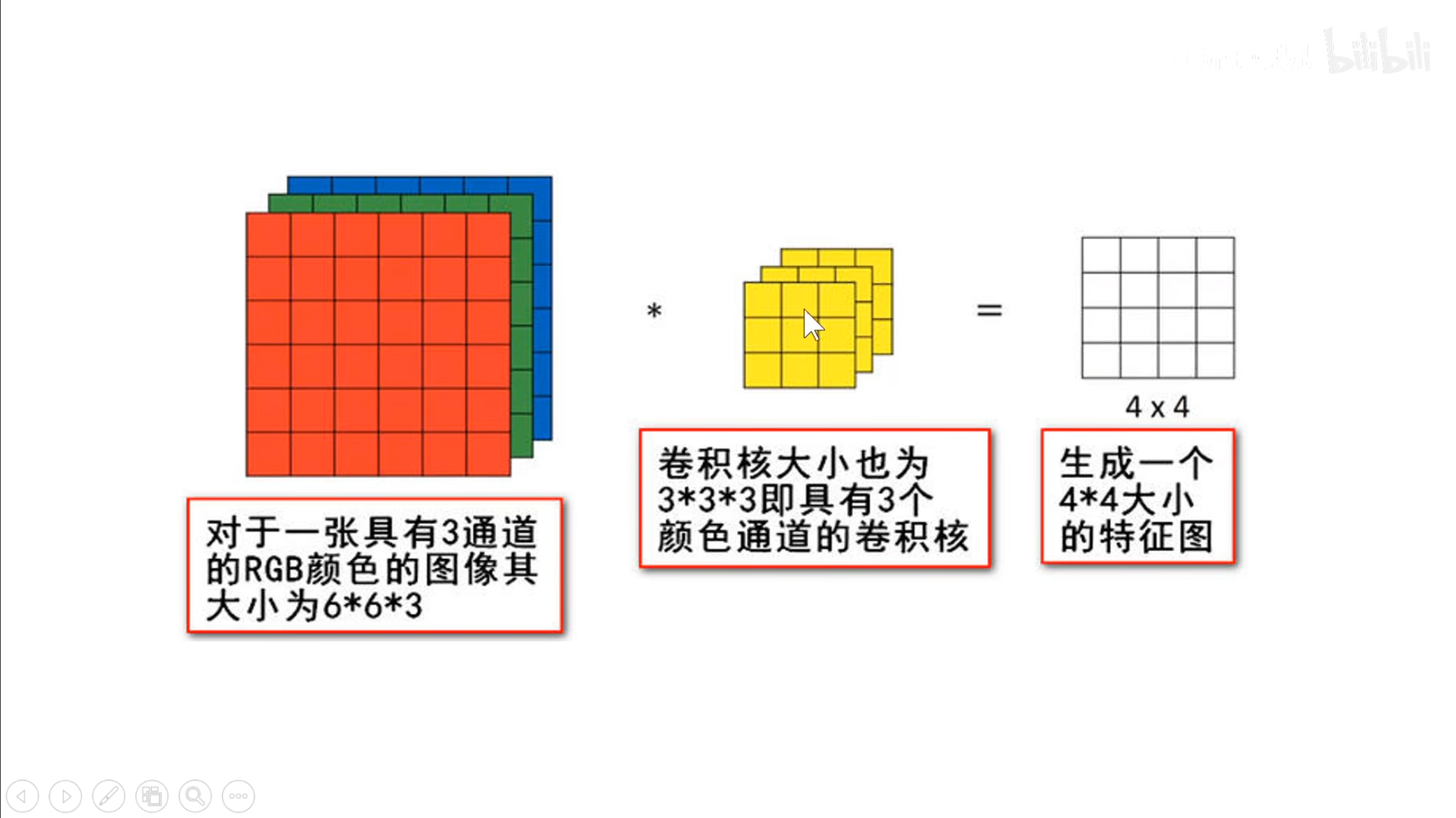
还需要注意的是,对于一个多通道的输入,对应的卷积核也要有相应的通道数,也就是对于一个三通道的输入,它的卷积核也要是三通道的。
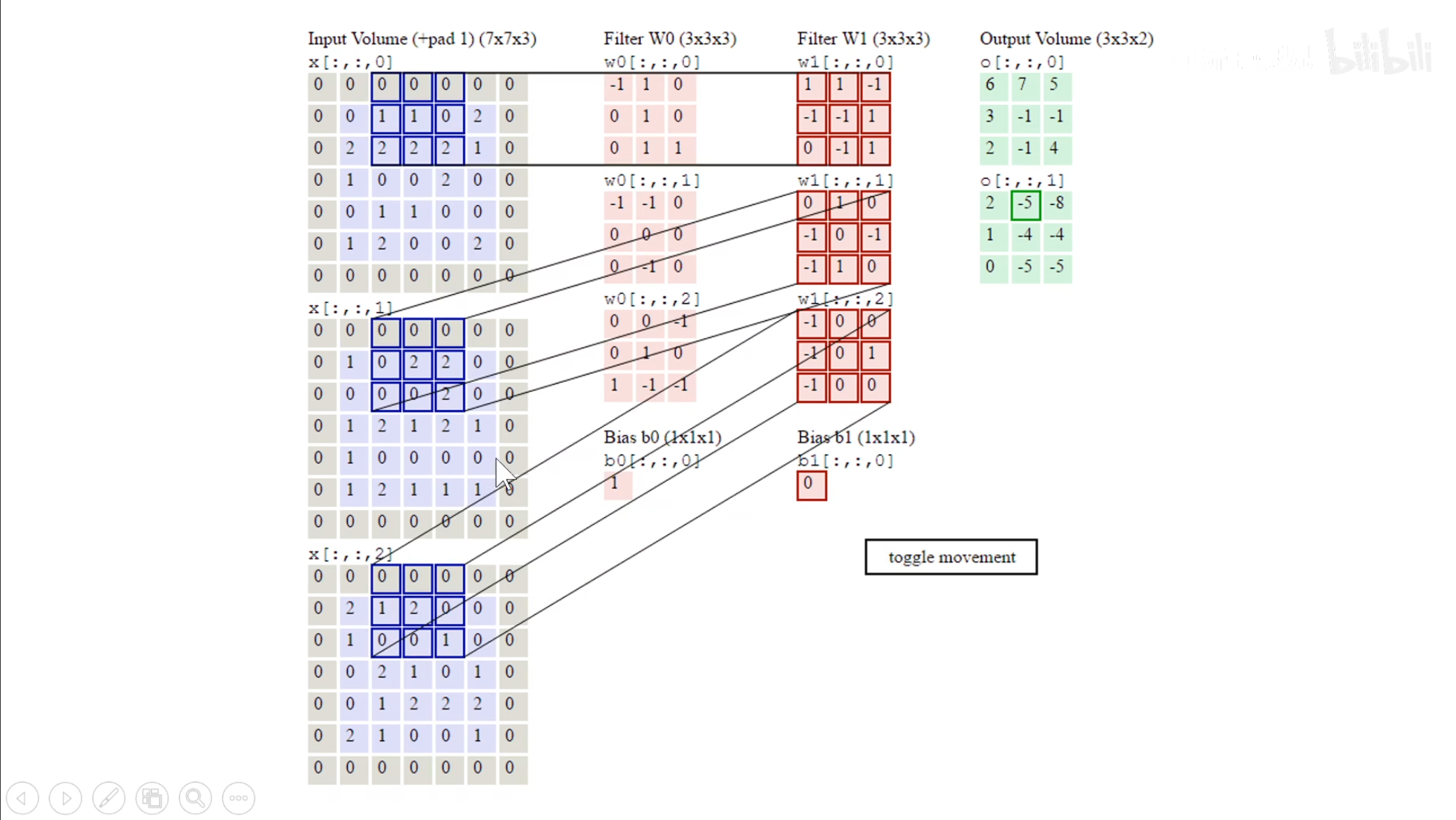
对应上图,也就是第二个卷积核正在生成第二个$ feature\ map $,有多少个卷积核就生成多少个$ feature\ map $,最终将这些$ feature\ map $摞在一起。
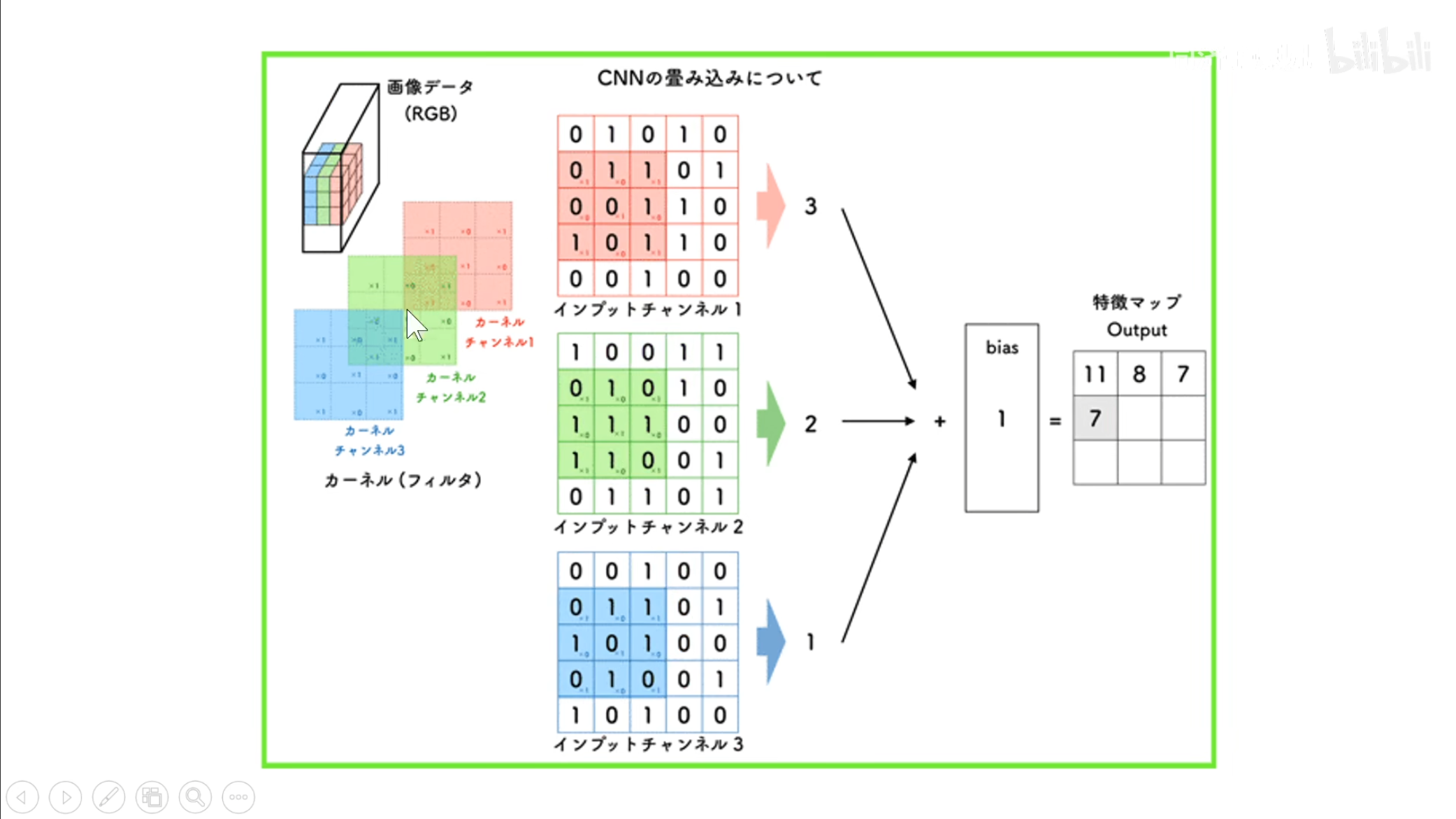
这个图和上一个相同,都是对于一个多通道的输入的一个处理,还可加上一个偏置项。

其实每一次的卷积操作都可以看成是一个全连接的神经元。
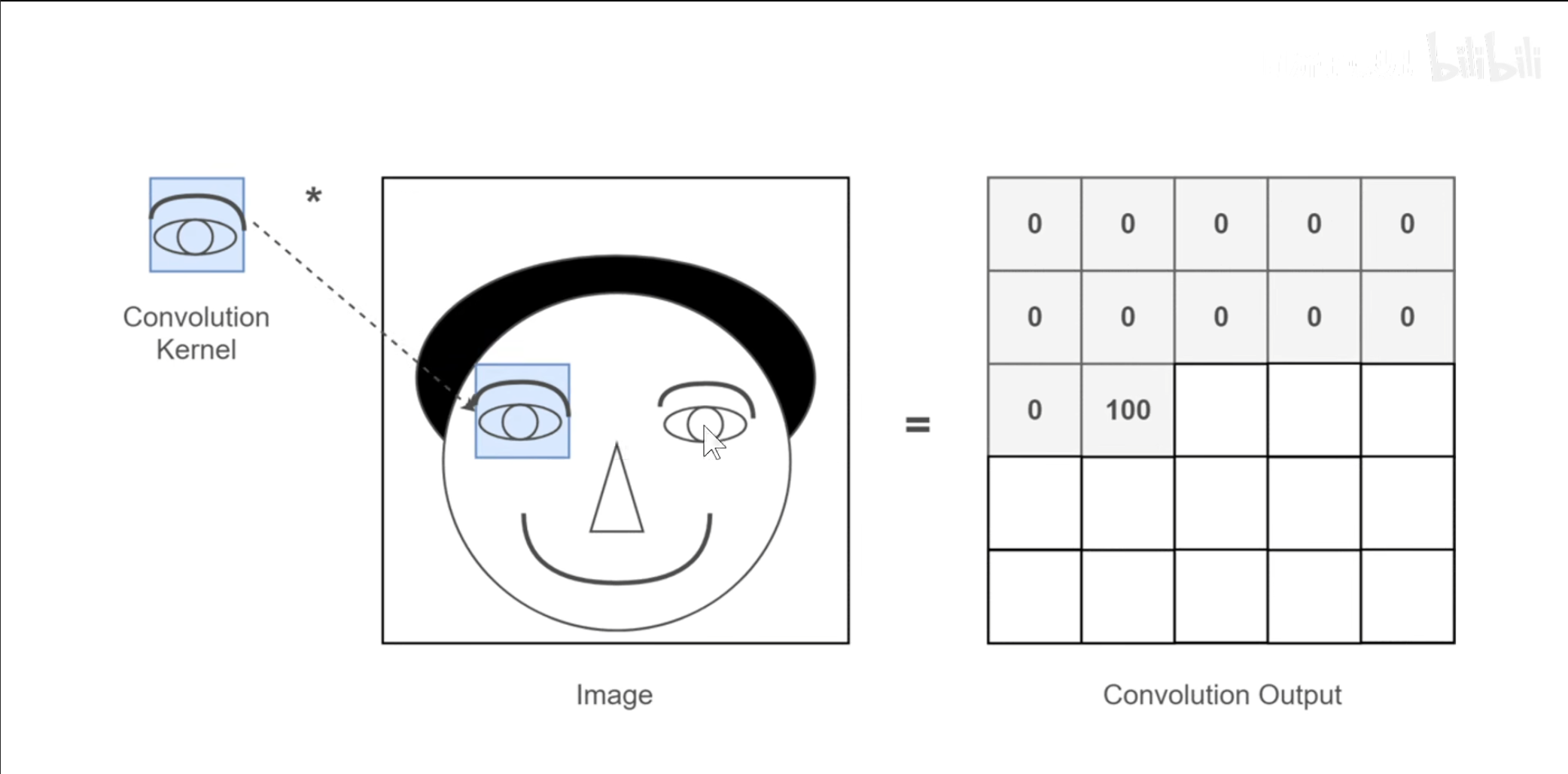
刚刚已经学习了卷积操作,但是还需要知道为什么需要进行卷积操作,卷积的意义就是将原图上符合卷积核特征的特征提取出来,例如上图中我们的卷积核就是一个眼睛,那么原图中眼睛的部分数值最高,
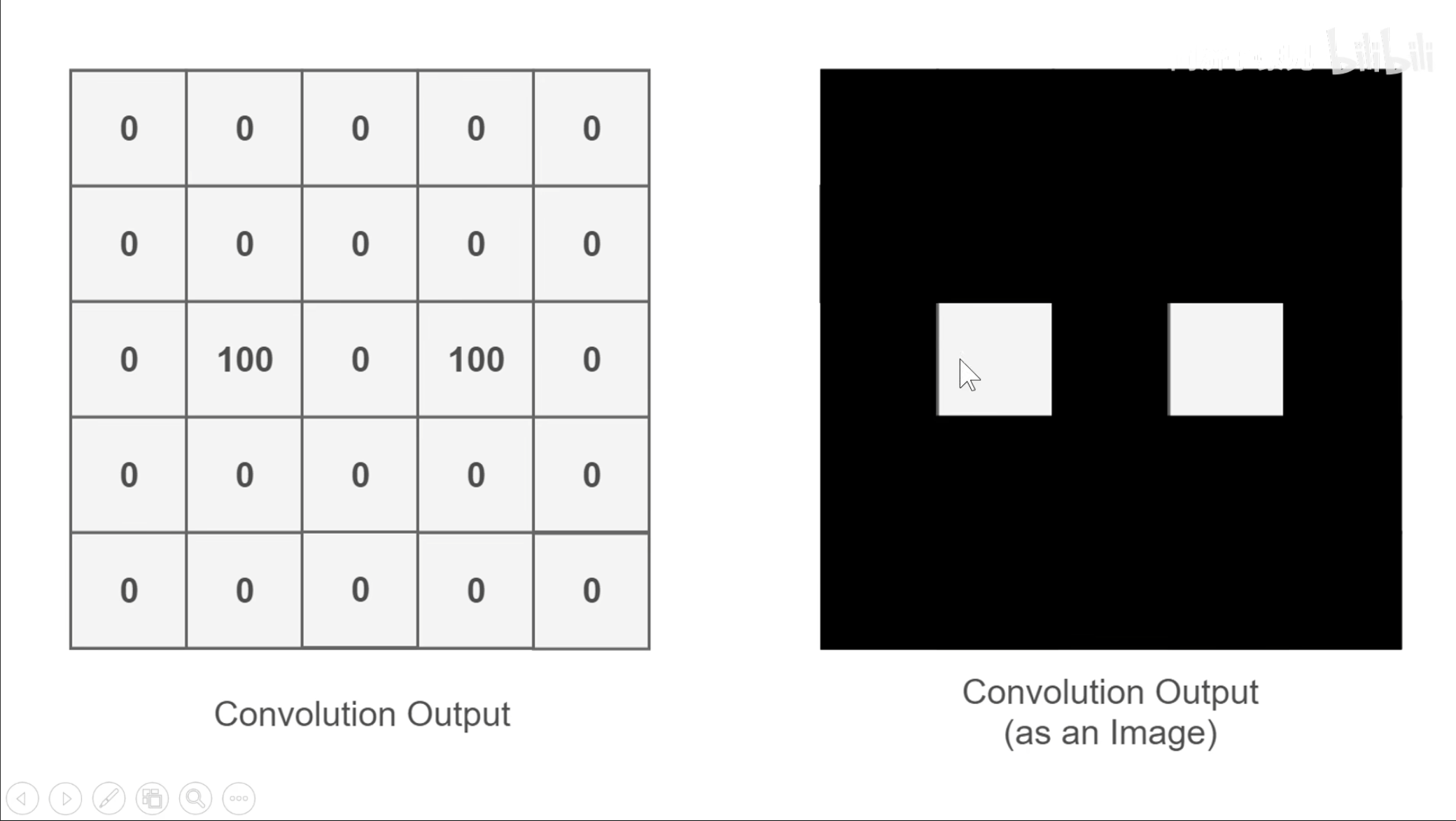
也就是得到这样的卷积输出,提取出眼睛的特征。
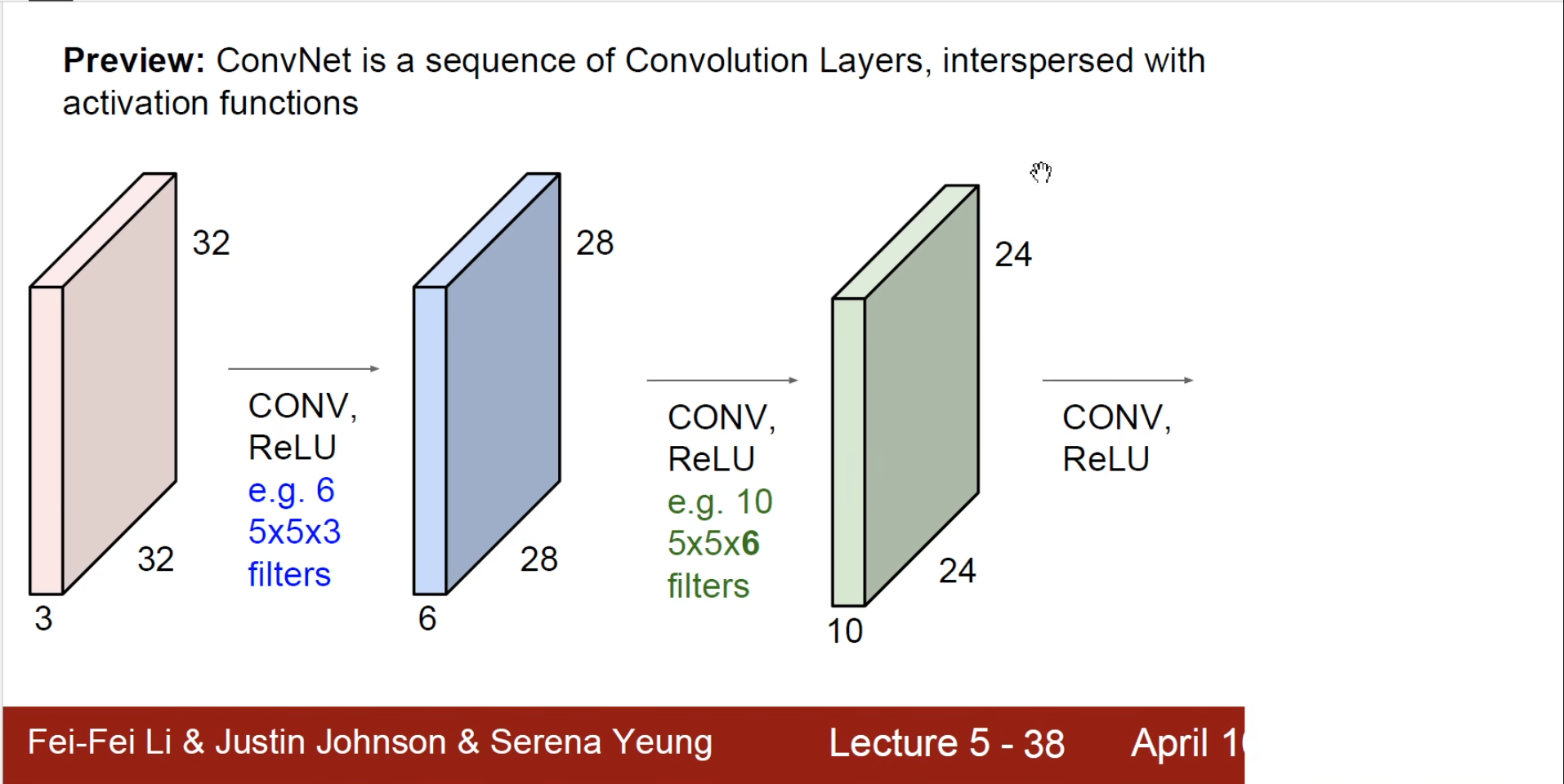
可以看到,有多少个卷积核那么久有多少个$ feature\ map $,那么如果具有$ 256 $个卷积核得到的$ feature\ map $就有$ 256 $,这样得到数据是很大的,因此我们可以选择其中的一部分,也就是用到了池化操作,也叫做下采样。
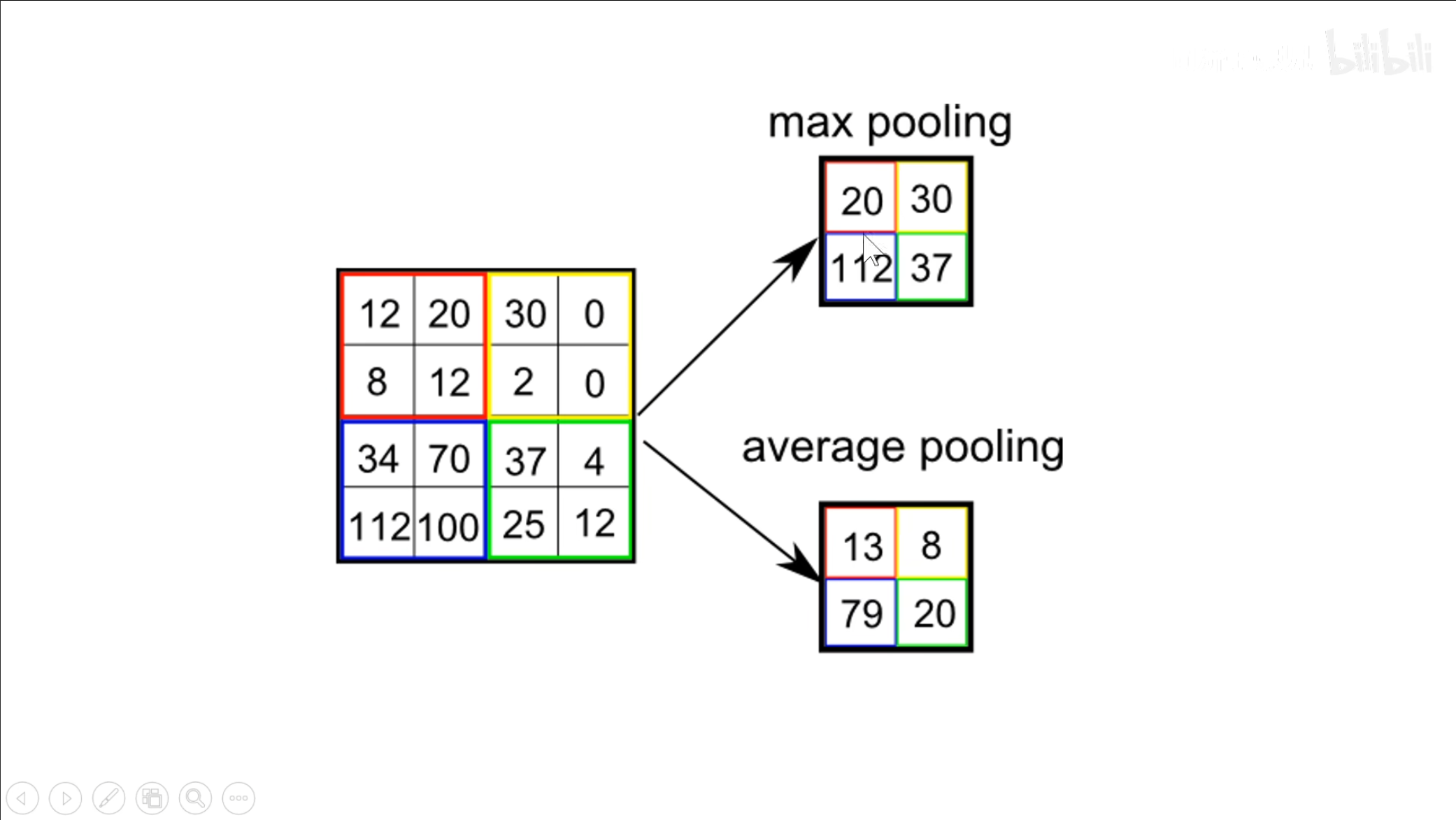
池化的操作有些类似于前面的卷积,但是没有卷积核,可以通过使用最大池化或者平均池化。
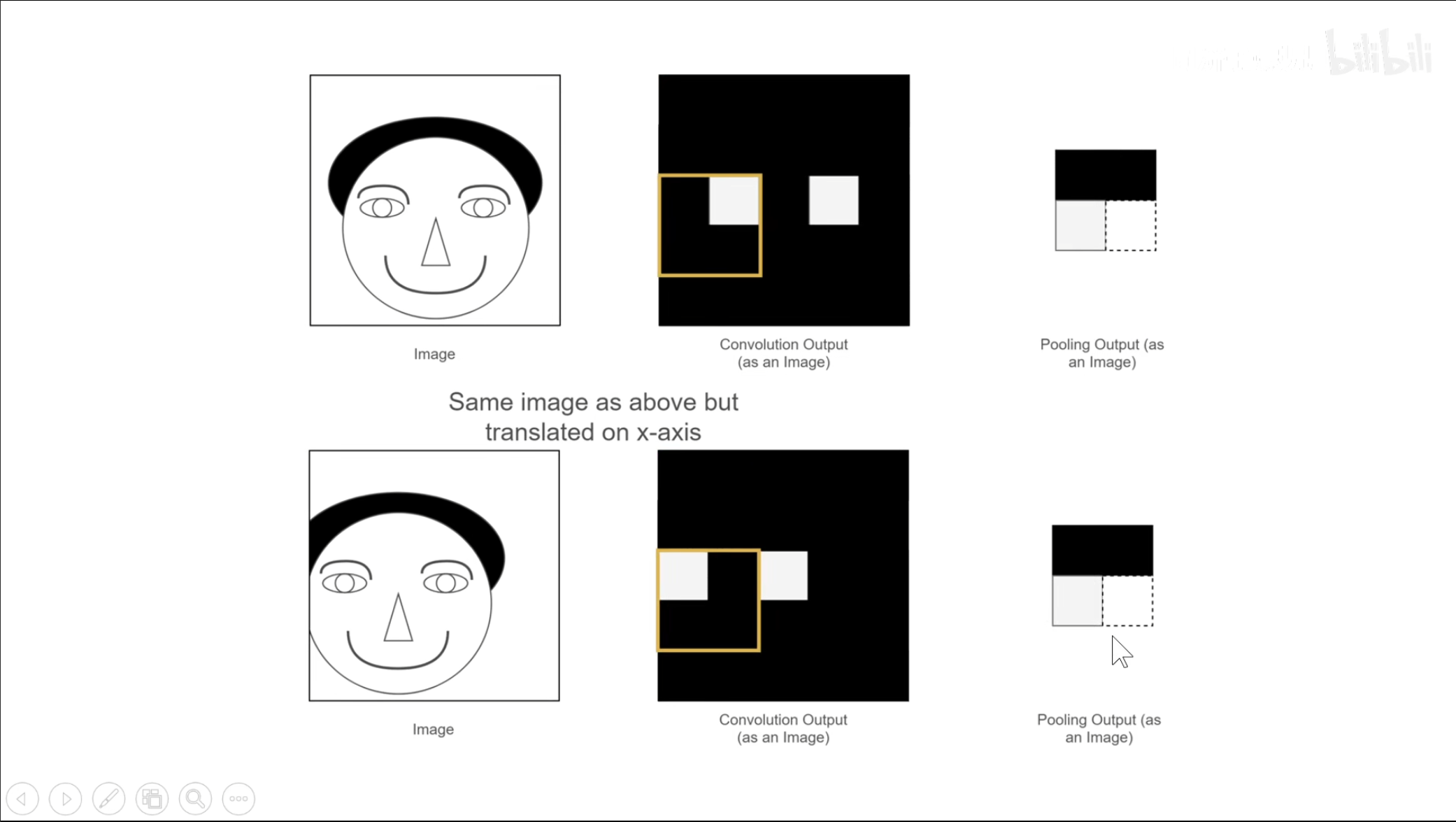
可以看到,即使原图发生了平移,但是我们提取到的池化之后的结果确实相同的,因此池化操作是具有平移不变性的,因此在识别图片时即使发生了偏移,伸缩也不会影响。
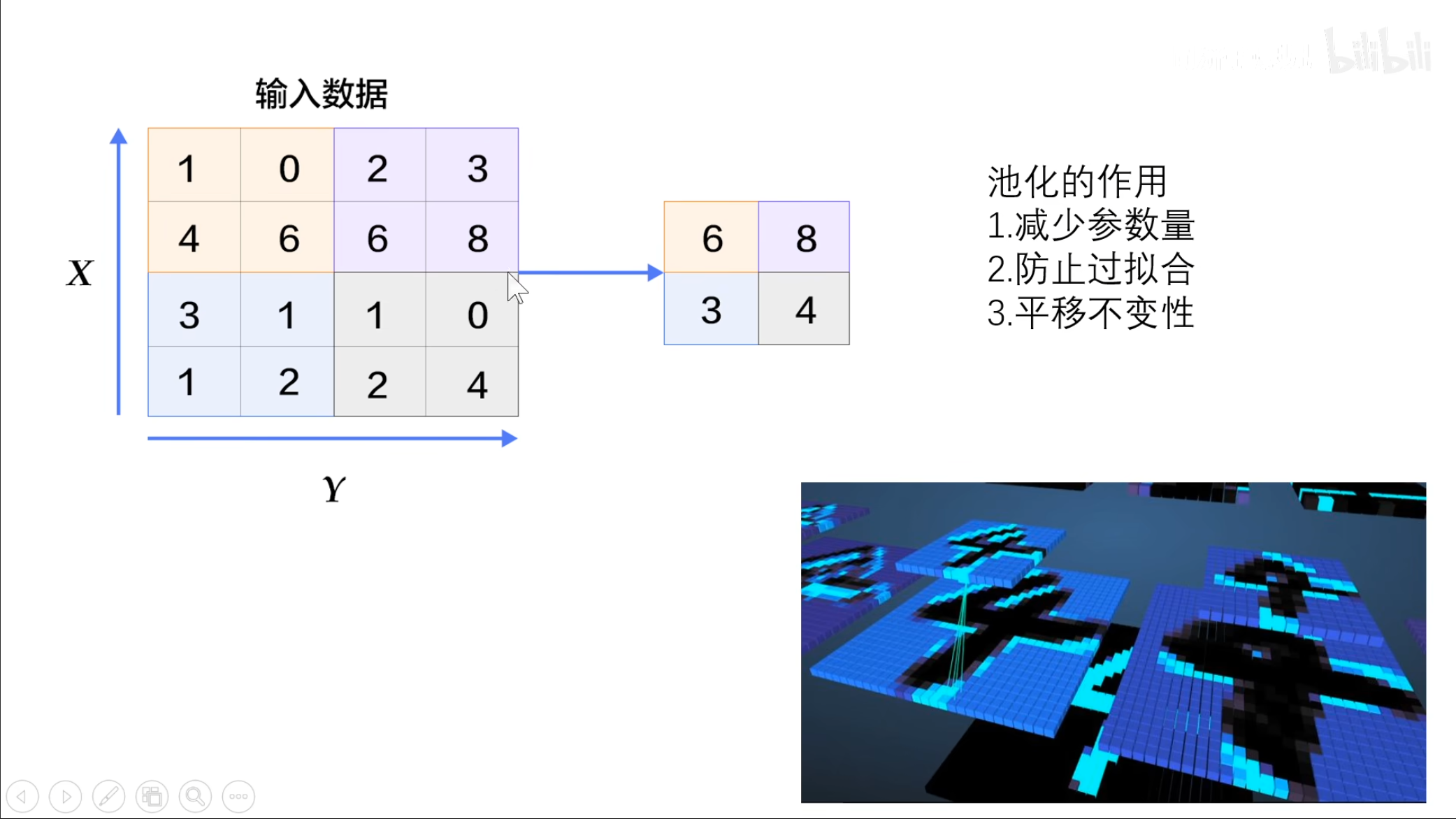
在池化中,除了刚刚提到的减少参数和平移不变性,还具有防止过拟合的性质,因为是提取了一个方块中最重要的信息,因此可以避免一些噪音点的干扰,可以避免过拟合。
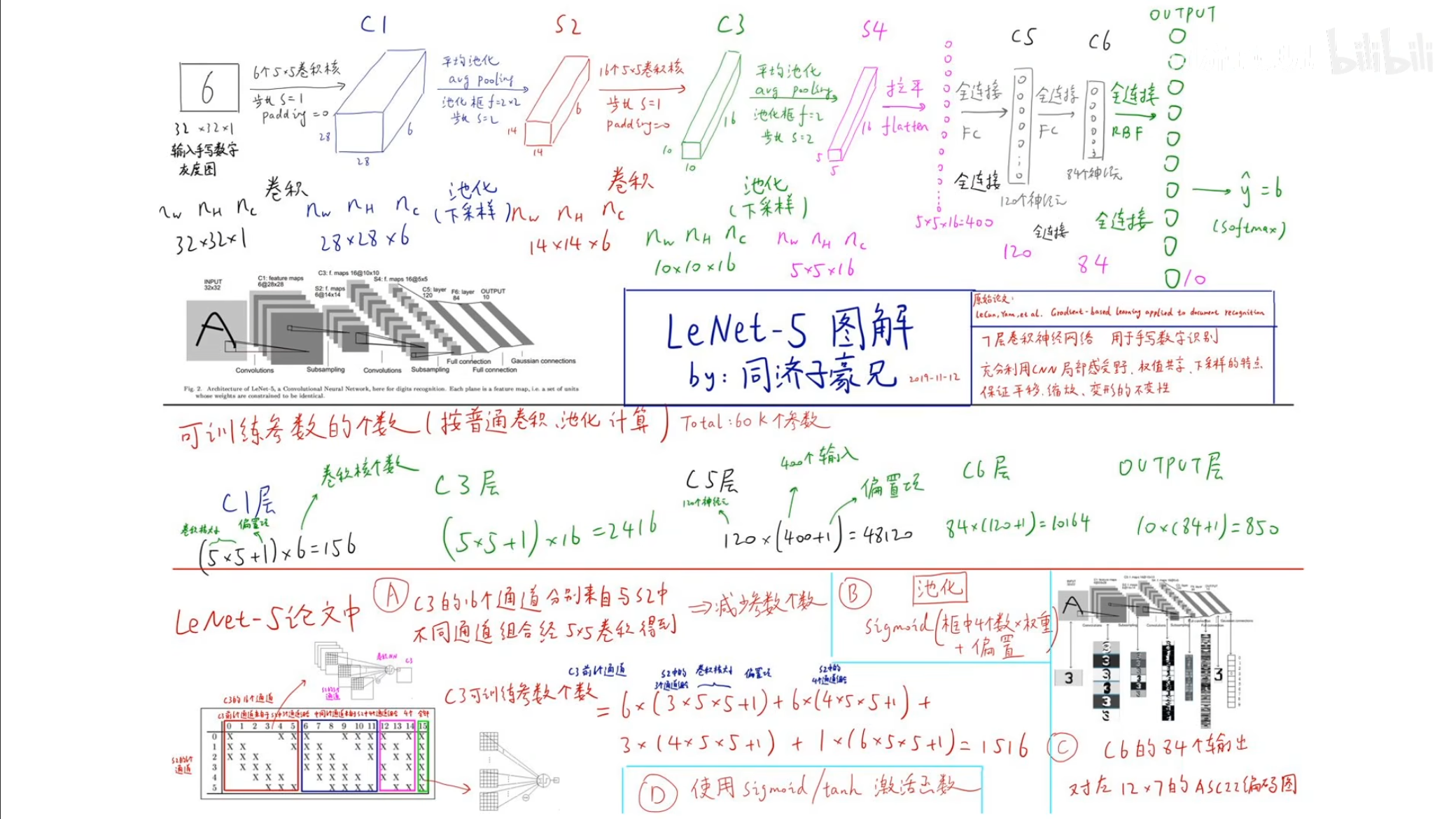
在这幅图中最上面可以看到卷积的过程,经过卷积,池化,最终全连接并使用$ softmax $输出。
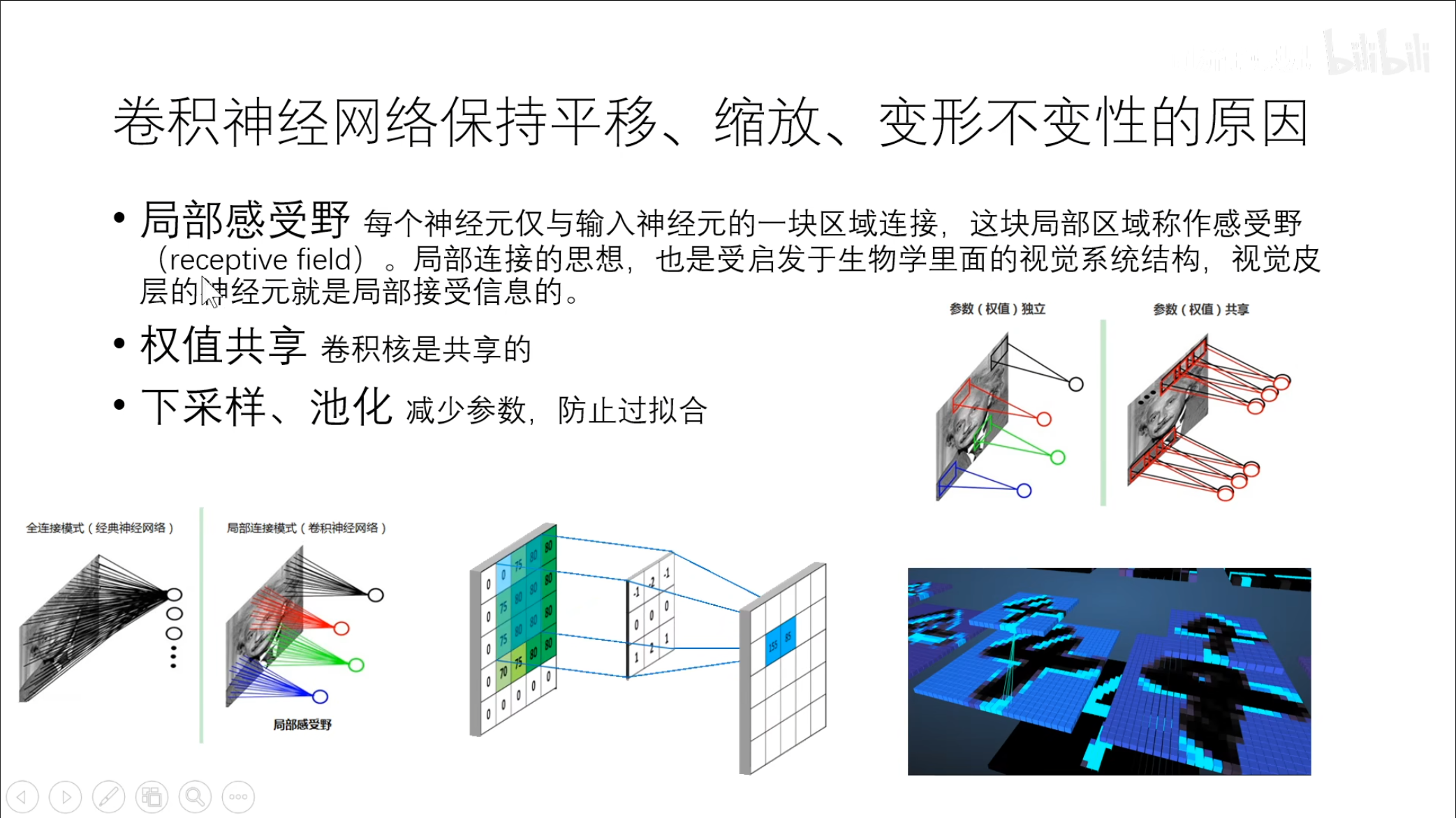
由于同一个卷积核在计算时是不变,因此说具有权重共享的性质。

对于如何计算一个$ feature\ map $的大小,可以通过$ (N-F)/stride+1 $这个计算公式进行计算,同时需要避免出现步长为小数的情况。

如果算上填充$ 0 $的情况就是加上双倍的$ padding $的大小,同时计算可得,当$ p=(F-1)/2 $时,输入和输出的长宽相等。

总结一下,通过上图计算我们可以得到输出的$ feature\ map $的大小和总权重的个数。
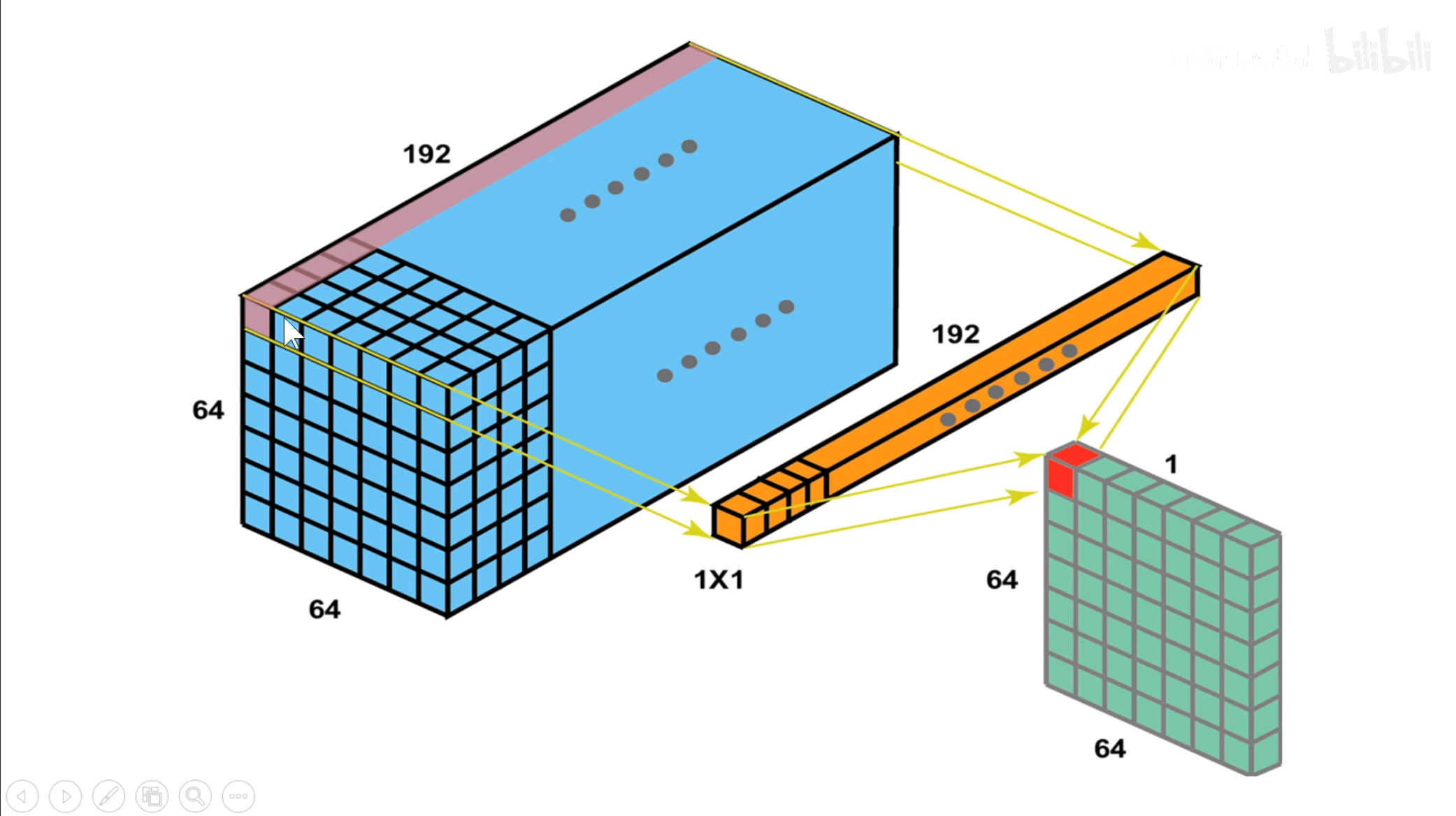
再试想一下,如果是一个$ 1\times1 $的卷积核,它具有什么作用。
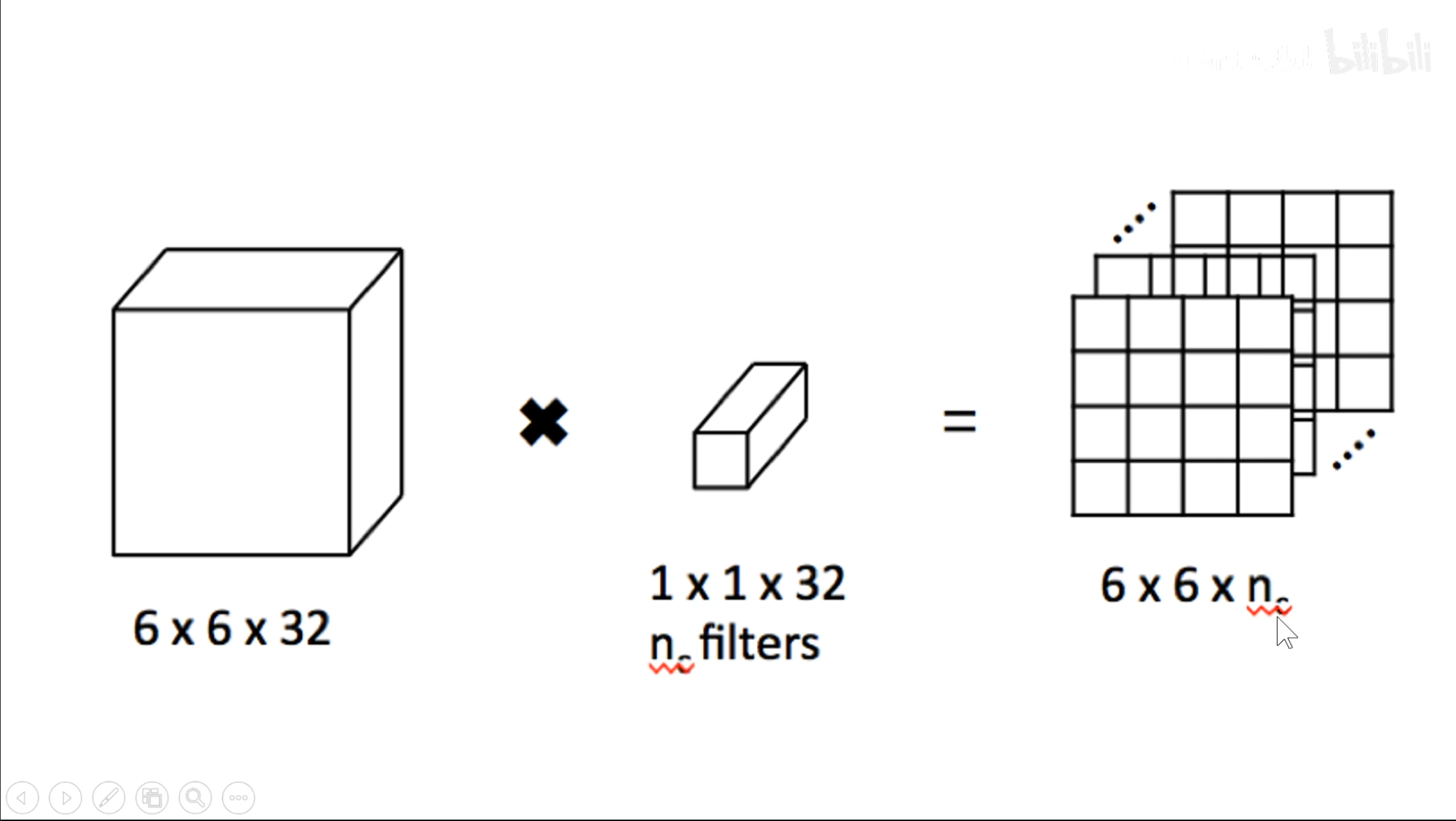
可以看到,这个卷积核具有升维或者降维的作用,当$ n $大于$ 32 $时就是升维,相反就是降维。
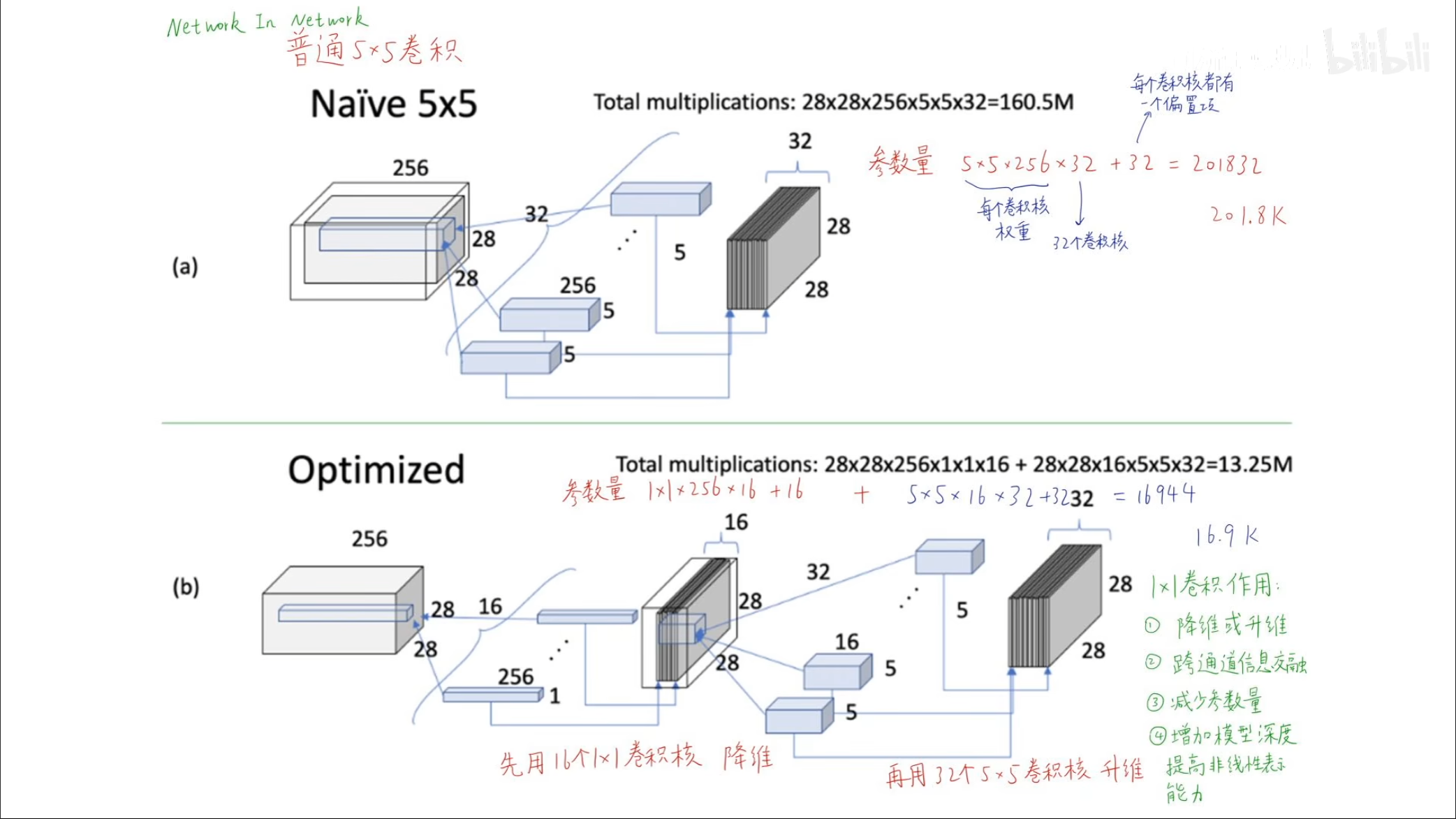
对于普通的卷积神经网络,计算的运算量是一个很大的数量级,但是如果可以通过$ 1\times1 $的卷积核进行降维,可以减少参数量,同时将不同通道之间的数据进行交流,加上一层降维操作也等同于增加模型深度,提高了非线性的能力。
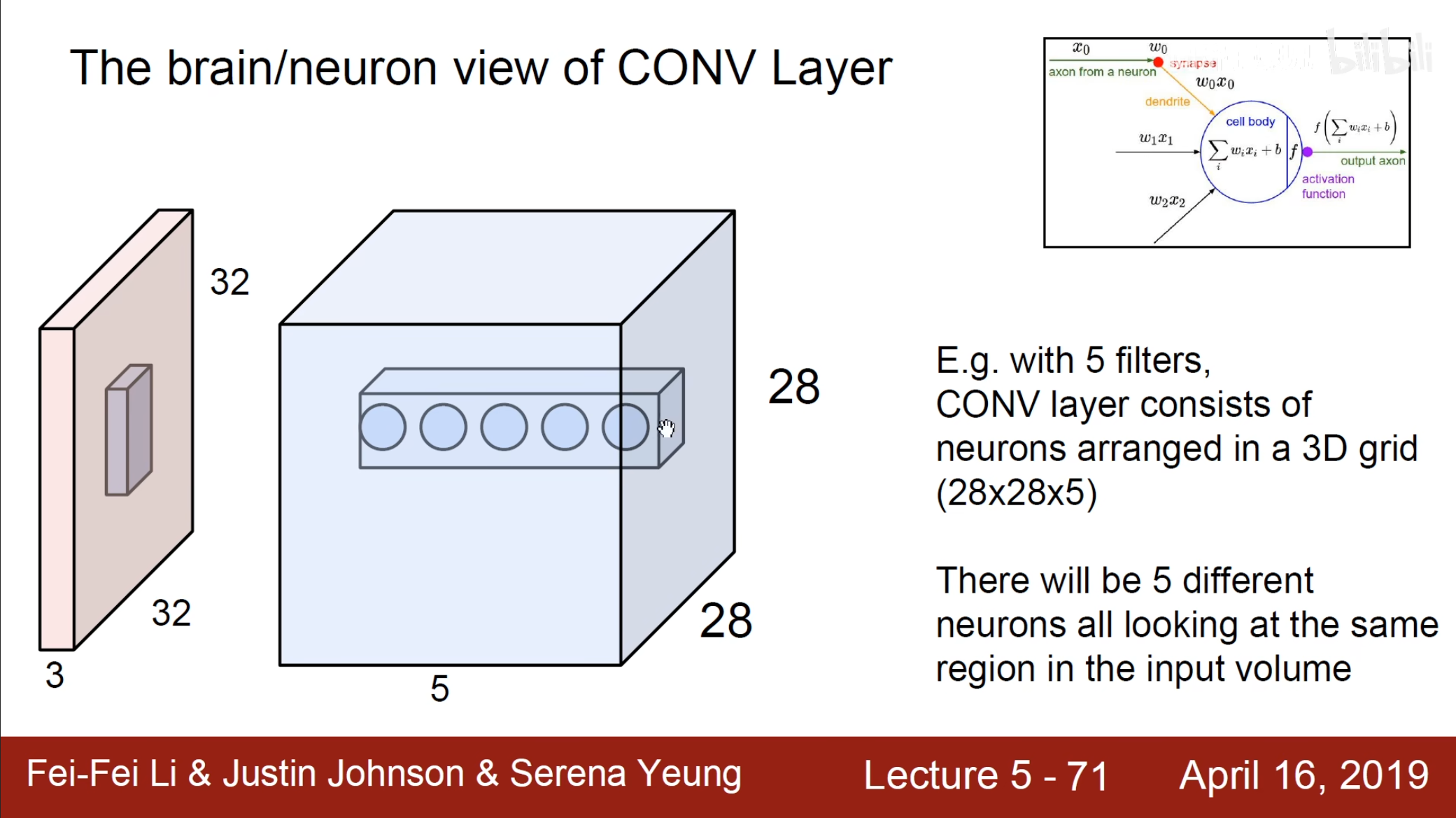
每一个卷积核也相当于一个神经元的全连接操作,其中原图上的元素相当于$ x $,卷积核上的权重相当于$ w $,一次卷积操作也相当于一个全连接操作。
对于图中的五个通道值,是五个不同的卷积核对于同一个感受野的计算值累加在一起,因此一个$ 1\times1 $的卷积核相当于对于不同通道的值穿在一起。
卷积和卷积神经网络
首先,我们通过两个图讲述卷积的概念。
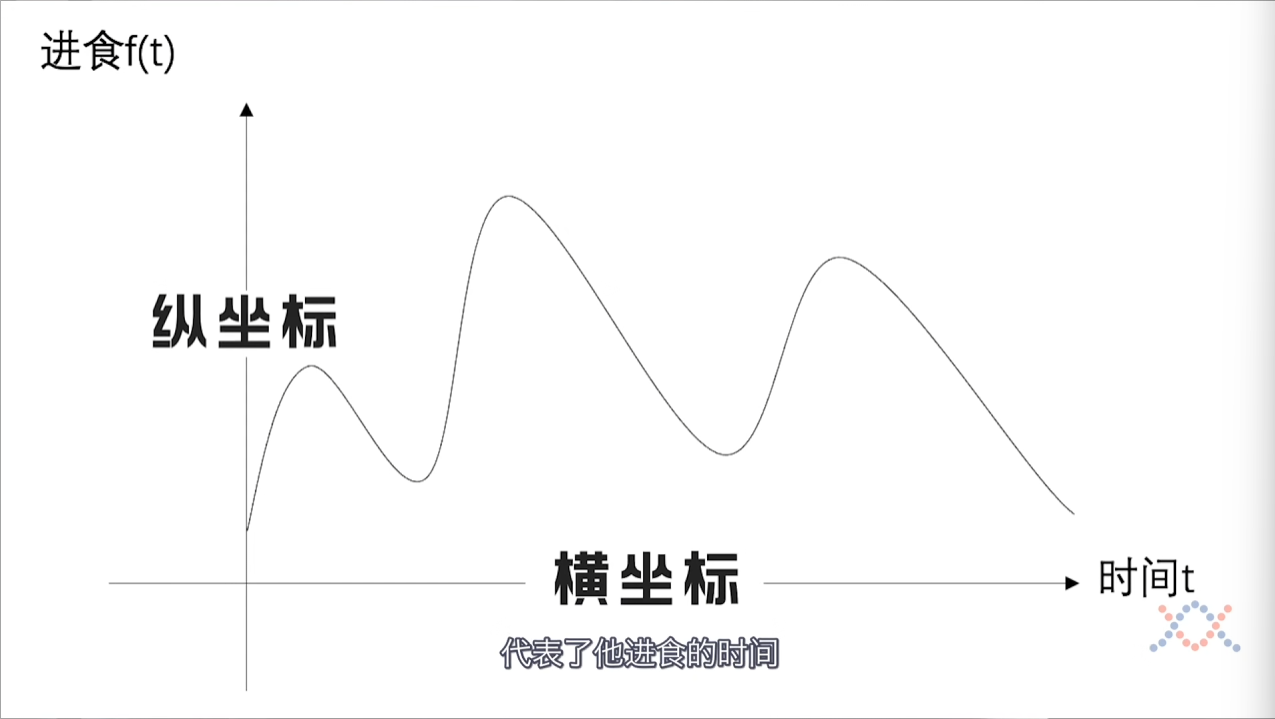
假设这是一个人吃食物的图像,横纵坐标分别代表时间和进食。
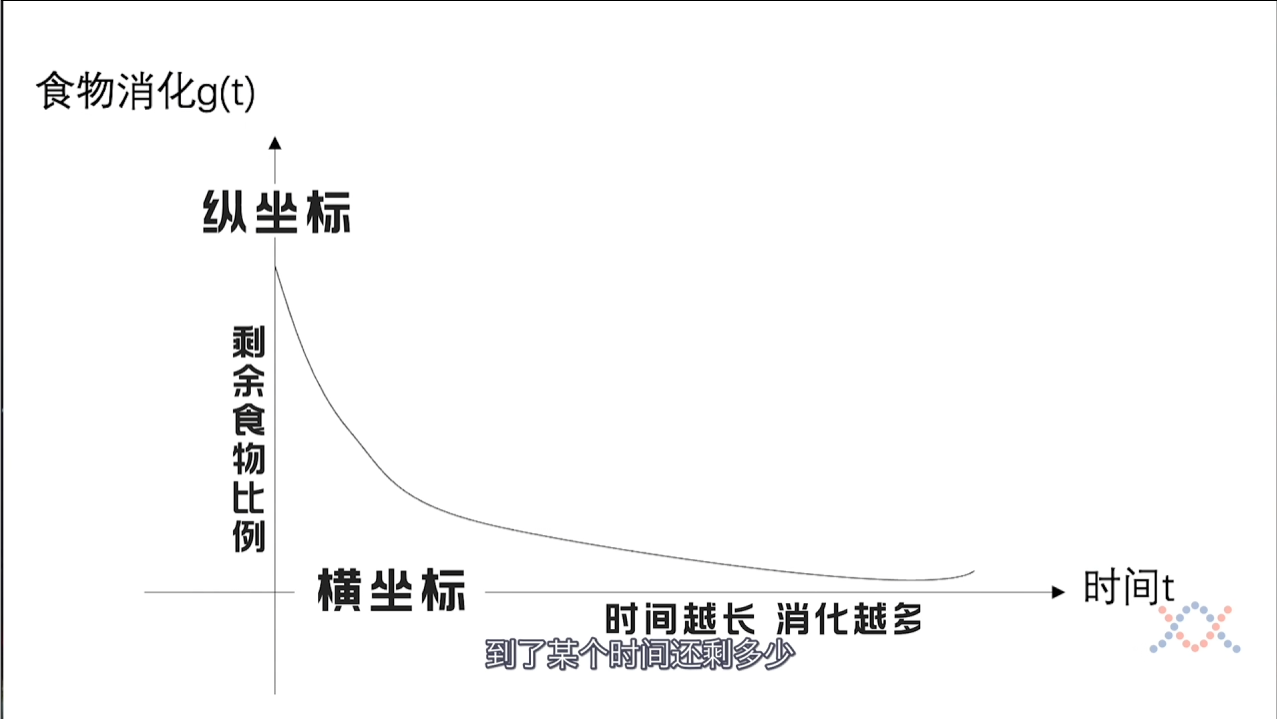
这是一个人消化食物的图像,横纵坐标分别代表时间和剩余的食物的比例。
对于卷积的公式,$ \int_{-\infty}^{\infty}f(\tau)g(x-\tau) \mathrm{d}\tau $,其中我们使用$ f $函数表示进食,使用$ g $函数表示消化。
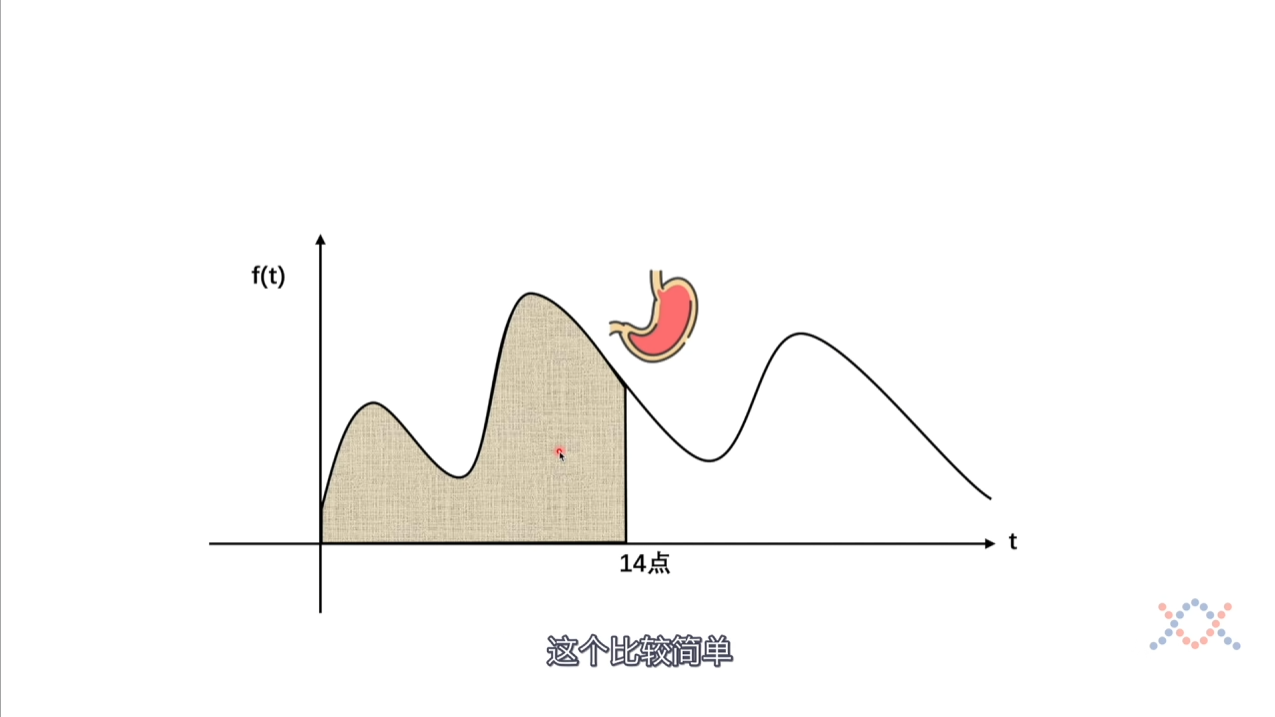
现在我们希望计算这个人在$ 14 $点剩余的食物,如果没有$ g $函数的话,我们仅仅需要求一个积分就行了,但是现在需要考虑到$ g $函数的影响。
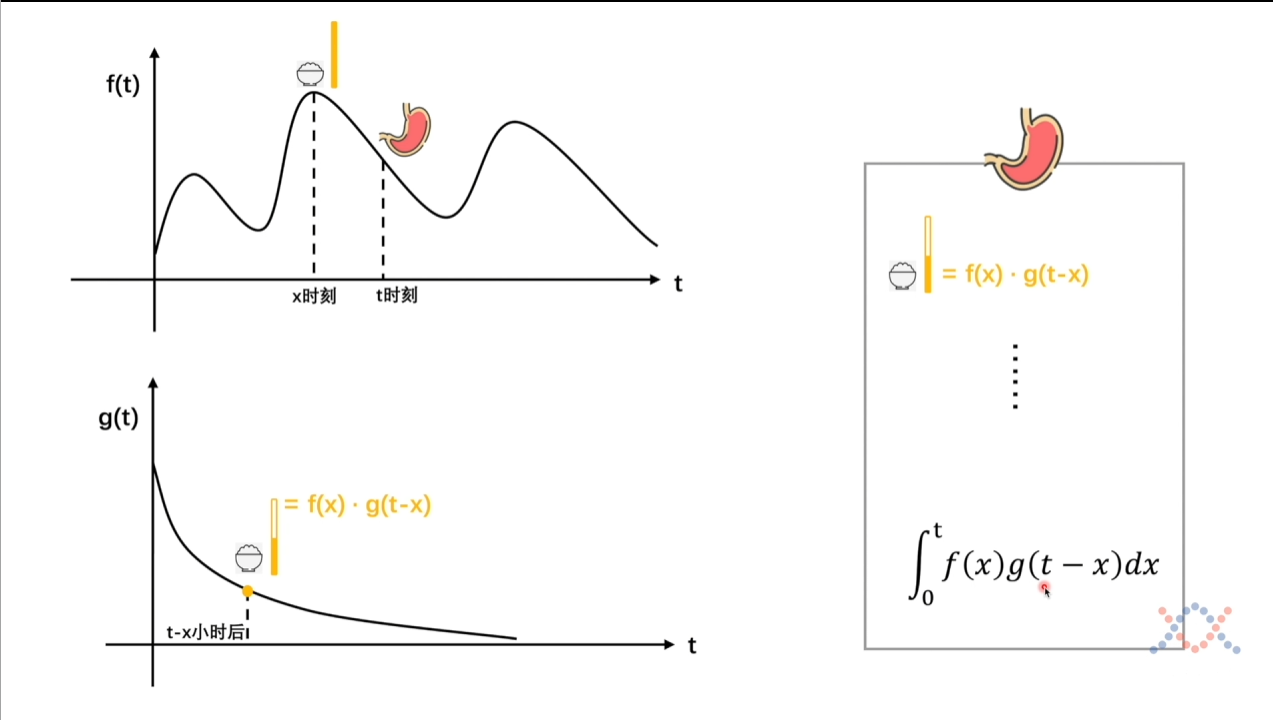
单个时间的话就是$ \mathrm{f(x)\cdot g(t-x)} $,但是全部加上就是$ \int_0^\mathrm{t}f(x)g(t-x)dx $。
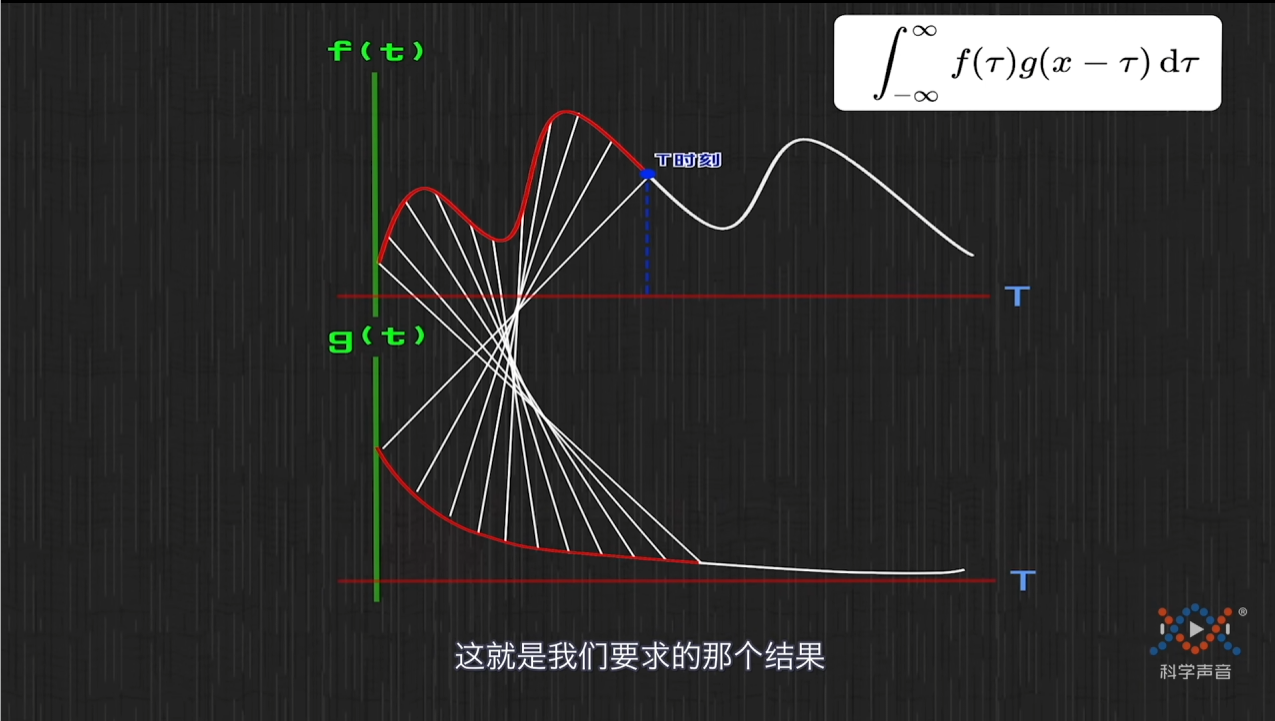
可以看到每一个连线就是$ f(x) $和$ g(x) $的相乘,最后把它们全部加起来,对比真正的卷积公式就是将上下限进行了调整。
现在我们可以得到卷积的价值,就是对于一个系统,输入不稳定,输出稳定,可以使用卷积计算系统的存量。
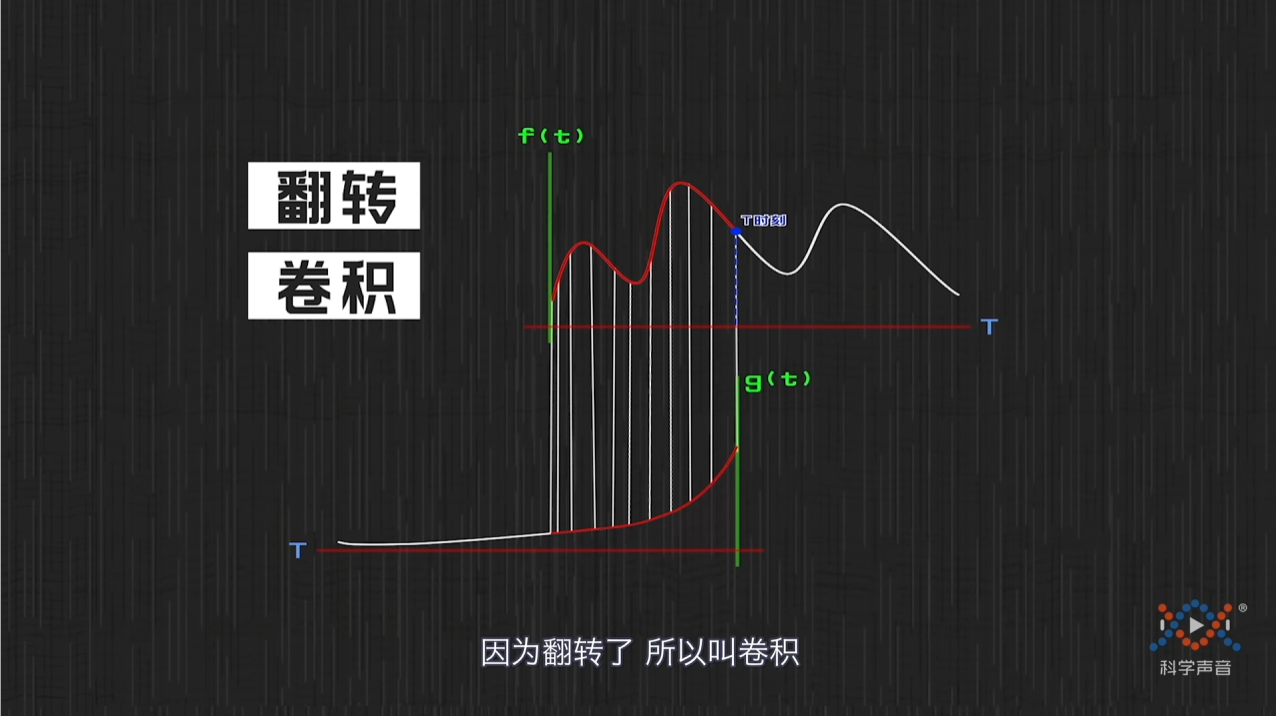
关于卷积的名字,有一个解释是将刚才的函数进行了翻转,因为翻转因此叫做卷积。

在卷积操作上,我们类比刚才的定义,输入就是图像本身,输出是卷积核。
但是为什么卷积核可以作为函数$ g $,关于这一点可以通过上面的图像进行分析,我们可以将其看作周围点对当前点的影响,假设当前点是$ f(x,y) $,周围点是$ f(x-1,y-1) $,那么代入也就是$ f(x-1,y-1)·g(1,1) $。
 将其全部展开的话,可以看到其实$ g $函数对应的就是卷积核,但是有一点别扭。
将其全部展开的话,可以看到其实$ g $函数对应的就是卷积核,但是有一点别扭。
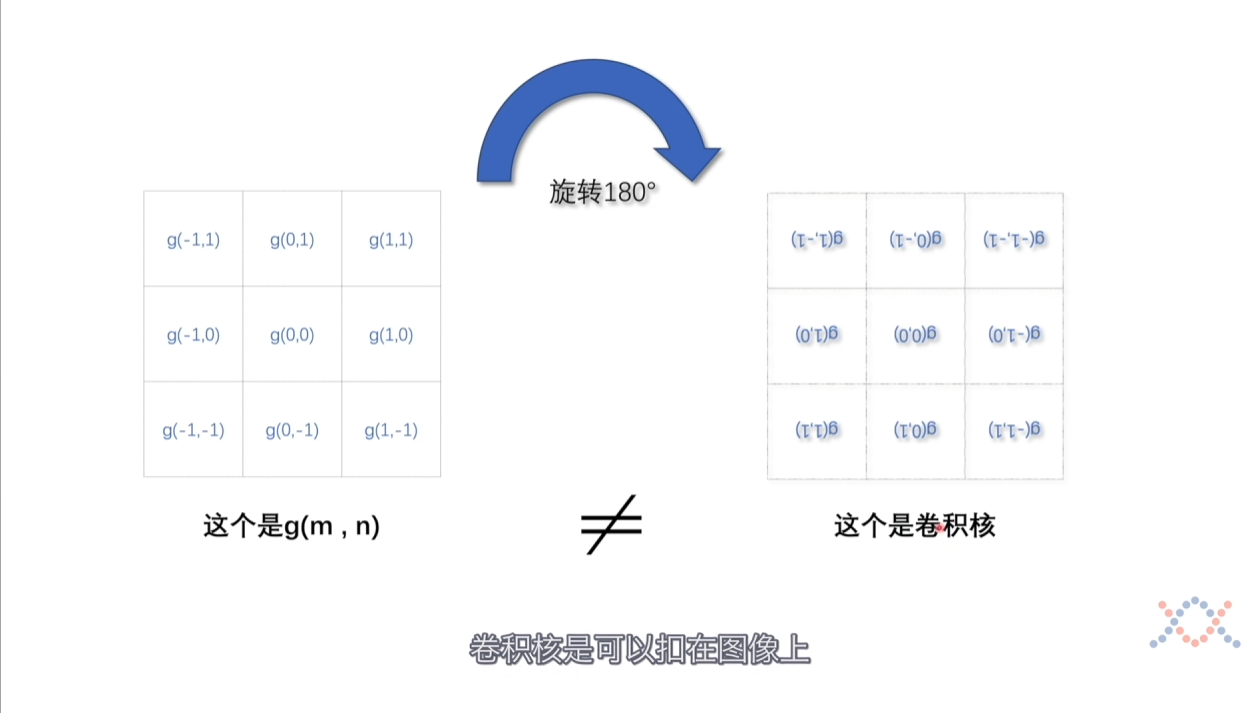
将$ g $旋转$ 180 $度就是卷积核本身了,我们可以使用这个卷积核对图像进行操作。
最后卷积在$ CNN $中可以看作是一个像素的对于周围像素点的试探和选择,可以通过这个卷积核作为一个过滤器,保留下有用的信息,提取一些和卷积核更相似的信息,例如上个小节提到的提取眼睛的信息。
对于卷积的含义有以下三层:
- 不稳定输入,稳定输出的系统中求系统存量
- 周围的像素点对当前像素的影响
- 一个像素点主动的保留周围像素点上需要的特征