图像分类:KNN和线性分类器
K-Nearest Neighbors算法
在$ cs231n $的课程中,首先介绍了$ k $近邻算法,但由于课件上没有介绍$ KD $树,因此采用另外一个课程的讲解。

首先,$ k $近邻算法的原理就在于找到离自己最近的$ k $个点,对于分类问题,采用多数表决法,对于回归问题,计算平均值,这里有些类似于决策树。
例如对于这个图像来讲,我们选择$ k $为$ 3 $,也就是离这个点最近的三个点,其中两个红三角,一个蓝方块,因此我们将其预测为红三角。

对于$ k $近邻算法分为这几个步骤,可以看到我们基本上没有学习的过程,相比于之前学到的逻辑回归,我们的训练过程仅仅是将所有的数据读入,因此$ k $近邻算法也被称为是一种懒散的学习方法,基本上不学习。同时我们也看到在$ k $近邻算法中,$ k $值的选取是十分重要的,接下来我们将介绍这个部分。
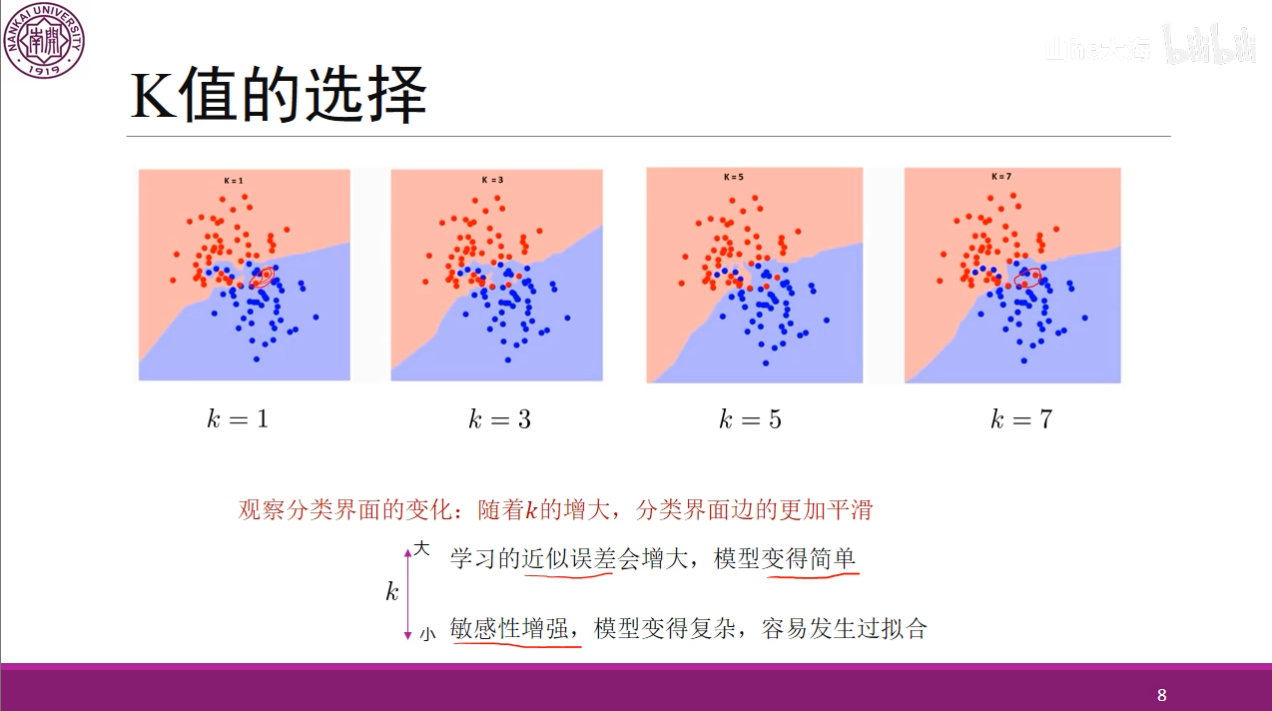
可以看到,对于不同的$ k $来讲,我们随着$ k $的增大,那么这个分类也就变得更加平滑,但是同时误差也会增大,如果使用一个极端的情况,$ k $等于样本个数,那么就没有分类,样本中哪个多就属于哪个,当$ k $太小时也不好,这样虽然误差减小,但是模型会过于复杂,很容易过拟合,因此,我们需要通过交叉验证选择一个合适的超参数$ k $。

除了$ k $的值,我们还需要选择怎么衡量这个距离,其中我们经常使用曼哈顿距离和欧式距离。
KD树

我们刚刚的计算方法也就是暴力的计算方法,但是在这种方法下,虽然我们的训练时间很短,仅需要将全部的数据读入即可,但是在测试中,对于每个测试数据我们都需要遍历全部的数据,如果这个数据集很大的话,我们的测试时间也会变得很大,为了解决这个问题,我们可以使用数据结构中的树。
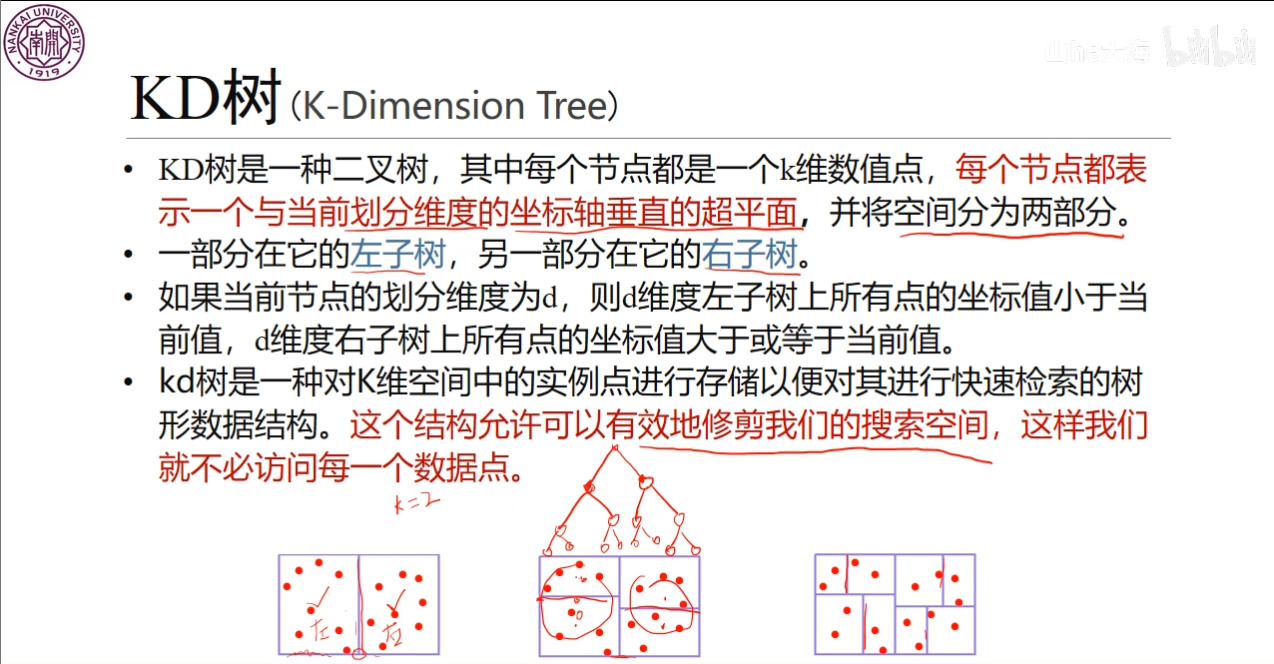
$ KD $树做作为一种二叉树,可以有效地划分数据集,避免对于全部的数据都进行访问。

首先,构建一个$ KD $树。我们先选择一个维度进行划分,我在不同的资料中找到两种划分的方式,第一种是视频中的这种方式,先选择$ x $轴,接着循环划分,如果有$ y,z $的话就一直循环,第二种是刘建平老师的博客中讲到,选择方差最大的维度作为划分,在本文中选择第一种方式,比较简单。
对于这个图,首先,我们以$ x $轴作为划分,因此,我们需要选择其中的中位数,这个例子中由于存在偶数个数,因此,我们可以选择$ (5,4) $也可以选择$ (7,2) $,我们选择较大的$ (7,2) $,接着,将$ x $轴上小于$ 7 $的$ (5,4),(4,7),(2,3) $划入左子树,将$ (9,6),(8,1) $划为右子树。接着在选择$ y $轴作为划分,最终可以得到下图。

图中在第三层就划分完成了,因此,如果还有数据的话重新选择以$ x $轴划分。

现在通过构建好的$ KD $树,介绍$ KD $树搜索。
当我们生成KD树以后,就可以去预测测试集里面的样本目标点了。对于一个目标点,我们首先在KD树里面找到包含目标点的叶子节点。以目标点为圆心,以目标点到叶子节点样本实例的距离为半径,得到一个超球体,最近邻的点一定在这个超球体内部。然后返回叶子节点的父节点,检查另一个子节点包含的超矩形体是否和超球体相交,如果相交就到这个子节点寻找是否有更加近的近邻,有的话就更新最近邻。如果不相交那就简单了,我们直接返回父节点的父节点,在另一个子树继续搜索最近邻。当回溯到根节点时,算法结束,此时保存的最近邻节点就是最终的最近邻。
虽然文字描述很绕口,但实际上的思路很简单,首先我们找到一个临时的最近的节点,也就是找到一个叶子节点,类似于二分搜索树,我们根据大于小于当前节点进行划分。
如图,$ (2,4.5) $在$ x $轴上,小于$ 7 $,因此,划分到左子树,又因为在$ y $轴上大于$ 4 $,因此划分到右子树,最终到达叶子节点$ (4,7) $。
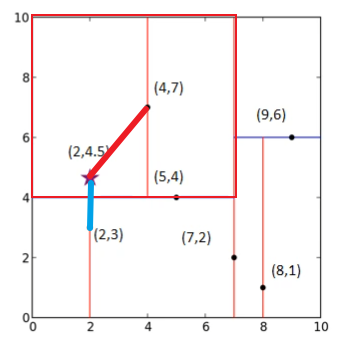
但是这仅仅是一个临时的最小值,我们可以看到$ (2,4.5) $虽然是属于$ (4,7) $所在的范围,但是由于这个范围太大,而这两个点离得并不是很近,反而是$ (2,3) $和$ (2,4.5) $离得更近一些。
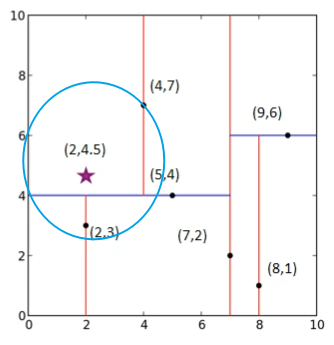
首先我们计算节点$ (4,7) $,可以看到,这个节点不小于我们的临时最小值,接着判断另一个兄弟节点$ (2,3) $所在的范围是否与以$ (2,4.5) $为球心,$ (2,4.5),(4,7) $之间距离为半径的超球体有相交的地方,虽然这个图我画的不是很标准,但是可以明显看到是存在一个相交的,因此我们需要将其移动到$ (2,3) $,经过计算,这个距离小于$ (4,7) $,因此将其更新为临时的最小距离,这个节点的兄弟节点已经判断过了,因此我们回到这个节点的父节点$ (5,4) $。
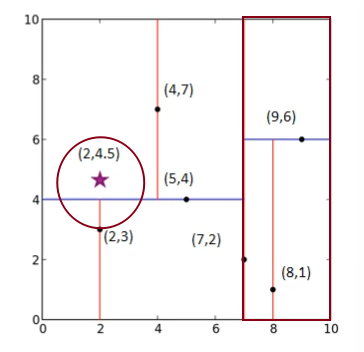
由于这个节点的距离不小于我们的临时最小值,因此不需要改变,同时这个新的超球体和当前节点$ (5,4) $的兄弟节点$ (9,6) $所在的范围也并不相交,因此不需要递归这个右子树,关于递归这个可以参照这篇博客的详细介绍,实际上就是重新按照第一步找到这个子树下的叶子节点。
kd tree最近邻搜索算法深度解析_kdtree最近邻算法-CSDN博客
接着回到根节点,计算这个距离不小于临时最小距离,因此搜索结束,则$ (2,3) $为最小距离节点。
通过了解了$ KD $树搜索最小距离,在计算$ k $个值时,仅需要屏蔽已经标记的最小距离重新进行循环计算$ k $次即可,同时,如果数据量不太,我们还可以通过维护一个小根堆来遍历一个即可。在使用$ KD $树中由于我们减少对于一些无意义的遍历,缩短了测试时间,但是数据分布不是很均匀的时候,这种方法的效果就不是很好了,对于这种情况可以参照这篇博客。
K近邻法(KNN)原理小结 - 刘建平Pinard - 博客园

我们虽然提到了$ KNN $算法,但是在实际的图像分类中我们并不会使用这个方法,除了这个方法在测试的时候太慢,还会出现例如上图中右侧三个图片虽然不一样,但是如果计算他们和左侧图片的$ L2 $距离却会出现一样值的结果。

同时当我们的维度提到了,需要的数据则是一个指数的增长,这些问题都导致我们在实际上并不会使用这个方法。
线性分类器
除了$ KNN $,我们还有一种分类方法,称为线性分类器,接下来从三个角度理解这个分类器。- 代数角度
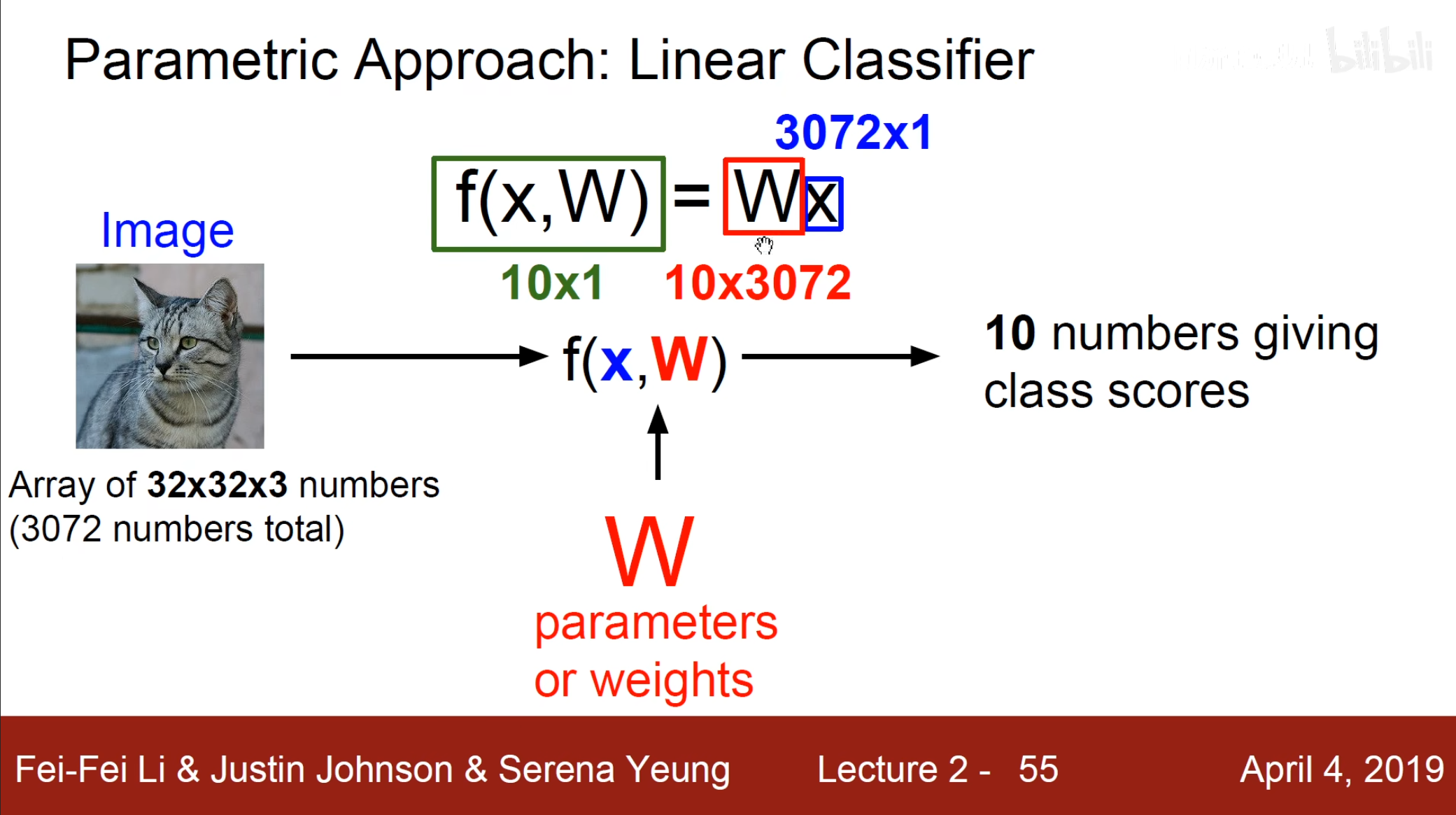
假设当前有一个长$ 32 $,宽$ 32 $,通道为$ 3 $的图像,将这个图像转换为一个列向量,也就是一个$ 3072\times1 $的列向量。同时我们将其分为$ 10 $类,对于每一个我们都需要$ 3072 $个权重,因此我们就得到了一个$ 10\times3072 $的矩阵,使用这个权重矩阵乘上像素值加上截距,也就得到了我们的分类结果。
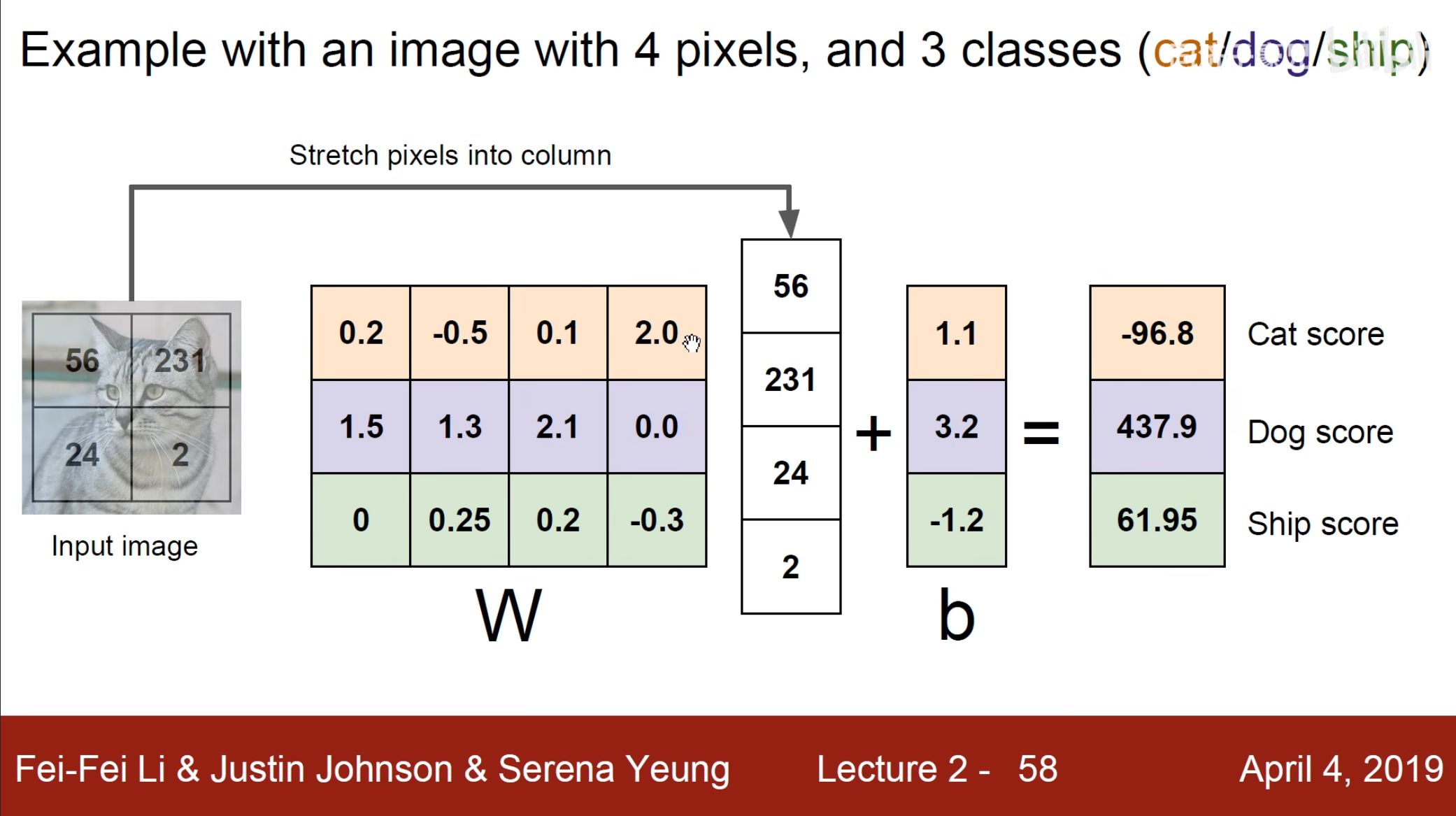
使用这个例子,我们猫的图片有四个像素点,因此就伸长为一个$ 4\times1 $的列向量,同时因为需要划分为$ 3 $类,因此需要一个$ 3\times4 $的权重矩阵,最后加上偏置即可。
- 直观角度

从直观角度上来讲就是讲训练的$ 3072 $个权重变回原本的$ 32\times32\times3 $的矩阵,可以看到对于飞机来讲蓝色像素点的占比分高,也就是讲如果有一个图片跟这个图片很接近,那么高的权重乘上高的像素自然结果也就越高,说明也就越是飞机。
- 几何角度
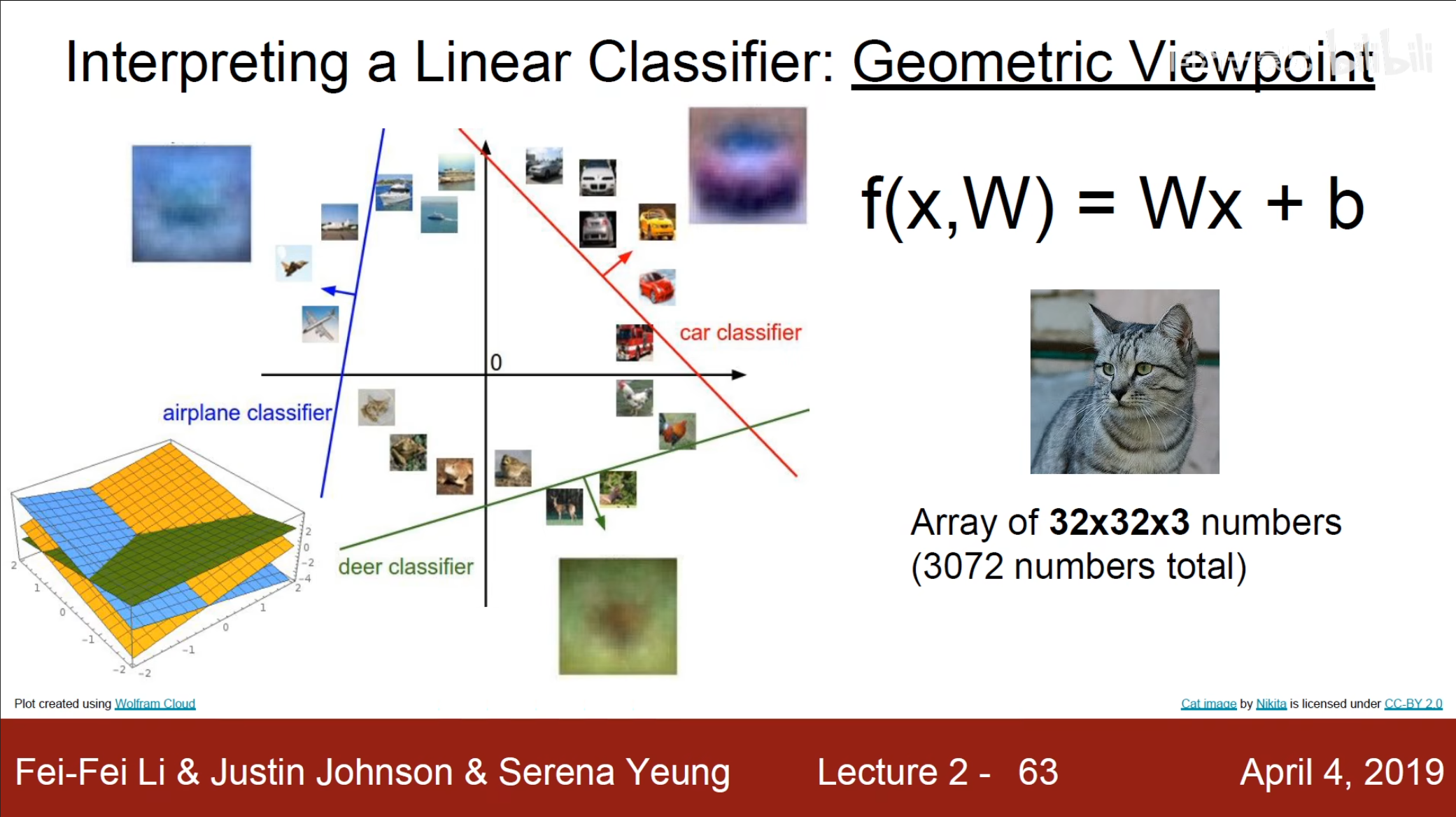
从几何上来讲,这个线性分类在一维上就是点,二维上就是直线,三维上就是面,更高维上就是超平面,例如上图中划分了$ 10 $个超平面。

同时线性分类也具有一些问题,对于线性不可分的情况,例如图一的异或问题,图二的环状问题,我们的线性分类都是无法满足的。
图像分类:KNN和线性分类器