支持向量机
硬间隔SVM-模型定义(最大间隔分类器)
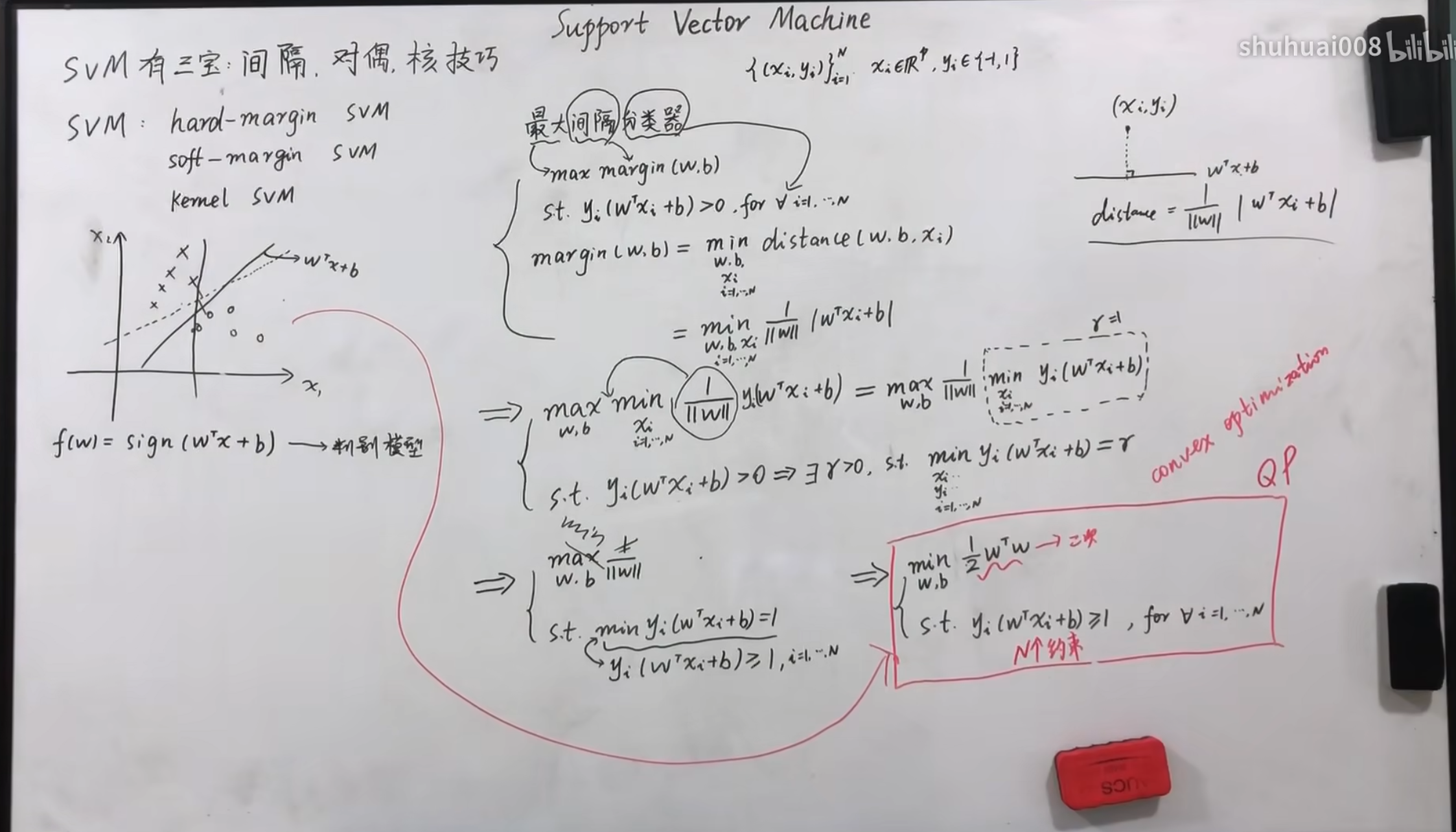
$ SVM $可用于处理分类问题,首先介绍硬间隔$ SVM $。
对于感知机分类来讲是存在多种分类方法的,但是这些分类中存在有的分类很容易发生变动,因此我们希望找到一个鲁棒性(稳定性)最好的一种。这里我们衡量的方法采用了硬间隔最大,首先选择在集合点中离分类超平面两侧中最近的点,这些点也被称为支持向量,相隔的距离也就是图中的$ margin(w,b) $。接着通过调整$ w,b $最大化该间隔。
其中我们处理要保证结构的最大化之外,也就是硬间隔的最大化,还要保证划分的点都是正确的,也就是$ y_{i}(w^{T}x_{i}+b) $的最小值大于$ r $,其中$ r>0 $,令$ r=1 $,将其缩放为一个固定的值,同时简化运算。
最终我们要满足在所有点都分类正确的情况下,最大化硬间隔。
硬间隔SVM-对偶问题引出

上一节介绍了硬间隔问题的数学模型,接下来对其进行一个转换,使其更加容易求解,同时可以方便使用核函数。
首先使用拉格朗日乘子,将其原本的约束条件改变为等式中的隐形条件,由于是$ min $最小化的值,因此,如果$ 1-y_{i}(W^{T}X_{i}+b)>0 $的话,我们对其进行$ max $,最终的值一定是$ +\infty $,但是加上前面的$ min $也就相当于直接将其省略,仅保留了$ 1-y_{i}(W^{T}X_{i}+b)<=0 $的情况。之所以要进行$ max $也是因为这个项是一个小于等于零的数,对其最大化相当于对于$ y_{i}(W^{T}X_{i}+b) $进行最小化。在这一步中其实就是相当于将这个带约束的条件转换为无约束的隐式条件。
接着我们利用这个凸二次优化问题本身的强对偶性,将其转化为$ maxmin $问题,利用图中右侧的转化,我们可以将等式最终简化为$ \min_{\lambda}\frac{1}{2}\sum_{i=1}^{N}\sum_{j=1}^{N}\lambda_{i}\lambda_{j}y_{i}y_{j}x_{i}^{T}x_{j}-\sum_{i=1}^{N}\lambda_{i} $,其中条件为$ \lambda_{i}>=0 $。关于这个条件的证明可以参照与这个视频。
硬间隔SVM-对偶问题之KKT条件

我们上一节已经得到了这个问题的对偶问题,现在我们需要利用它的$ KKT $条件。
由于原问题和对偶问题之间具有对偶性是满足$ KKT $条件的充要条件,我们已经知道由于这个问题是凸二次优化问题,一定满足强对偶关系(这一点我也不会证)。
因此我们就可以利用$ KKT $的条件,因此我们就可以计算$w^*,b^*$的值。
其中$w^*$已经计算过了,而对于$b^*$就需要利用我们的$ \lambda_{i}(1-y_{i}(w^{T}x_{i}+b))=0 $这个松弛互补条件,最终通过右下角的推导可以得到$ b^{*} $的值。
对于这个松弛互补条件,如果我们的点在$ w^{T}x_{i}+b=\pm1 $上,那么$ 1-y_{i}(w^{T}x_{i}+b) $就等于$ 0 $,$ \lambda>0 $,但是如果不再这个分界上,那么$ 1-y_{i}(w^{T}x_{i}+b) $就小于$ 0 $,那么$ \lambda=0 $,那么对于求解$w^*,b^*$就无意义了。
软间隔SVM-模型定义

前几节中介绍了硬间隔$ SVM $,现在我们来介绍软间隔$ SVM $。
如果我们的数据中存在噪音的情况,那么我们就需要对超平面进行调整,现在我们需要这个模型可以容纳一些错误,也就是引入损失函数,现在这个函数有两种定义的方式。
如果使用数量代表,那么可以通过指示函数$ I $表示,但是由于这个函数不是连续的,因此我们在进行求导的时候很不方便,因此可以使用距离表示。
如果$ y_{i}(w^{T}x_{i}+b)>=1 $,那么$ loss=0 $。如果$ y_{i}(w^{T}x_{i}+b)<1 $,那么$ loss=1-y_{i}(w^{T}x_{i}+b) $。也就可以写成$ loss=max{0,1-\underbrace{y_{i}(w^{T}x_{i}+b)}_{z}} $,由于这个函数的图像类似于一个合页,因此也被称为$ hinge \quad loss $,即合页函数。
同时由于使用$ max $的表达不太方便,因此可以引入一个$ \epsilon $,因此我们的表达式也就可以写成下面的形式。
$\begin{cases}\min_{w,b}\frac{1}{2}w^Tw+C\sum_{i=1}^N\epsilon_i \newline s.t\quad y_i(w^Tx_i+b)\geq1-\epsilon_i,\epsilon_i\geq0\end{cases}$
核方法-背景介绍

之前我们介绍的硬间隔是对应严格线性可分的情况,为了允许一定的错误我们引入了软间隔,但是如果当错误过多,已经是非线性可分的情况,那么我们就需要改变思路。对于感知机来讲,我们可以使用升维或者采用多层感知机,也就是神经网络来逼近任意一个线性函数,对于$ SVM $来讲我们可以也可以使用升维的方法。
可以看到在之前的对偶问题转换之后我们得到的结果中存在一个内积的情况,那么在升维之后这个内积就会变成$ \phi(x_{i})^{T}\phi(x_{j}) $的形式,对于少数的样本点进行升维的转化还可以接受,但是对于多个样本点我们很难计算升维的转换,因此我们可以使用一个核函数,不需要升维,直接计算最终的升维之后的内积。例如我们使用这个$ exp(-\frac{(x-x^{\prime})^{2}}{2\delta^{2}}) $这个核函数就可以直接计算最终的结果,而不需要进行复杂的升维,大大简化了运算的过程。
核方法-正定核(两个定义)
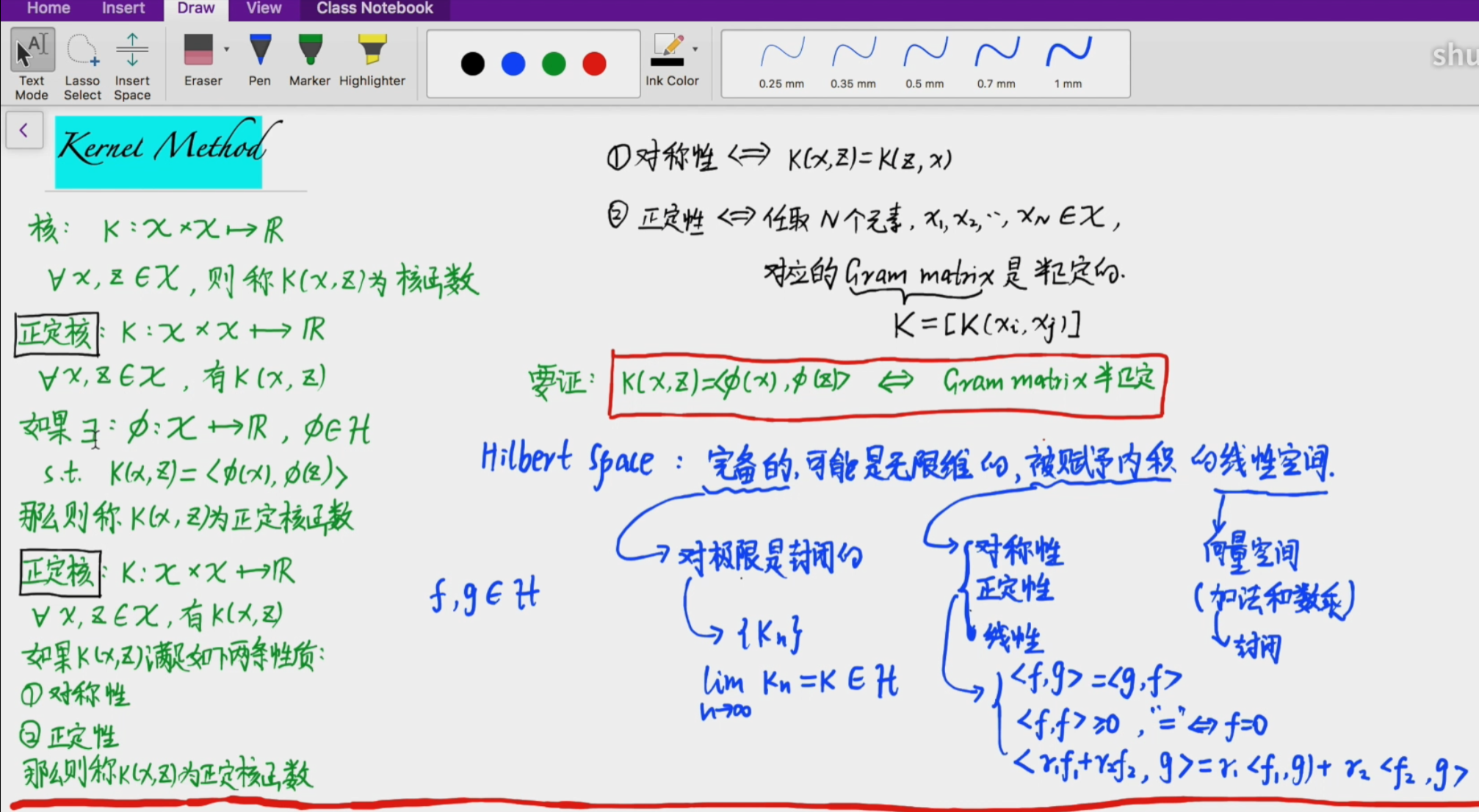
对于正定核,具有上图的两个定义,第一个表示对于一个正定核函数,通过核函数计算的值等于经过映射之后的内积的值,但是这个不利于计算,因此有第二个定义,也就是满足核函数满足对称性和正定性即可证明该核函数为正定核函数。下图给出两个性质的证明。

补充
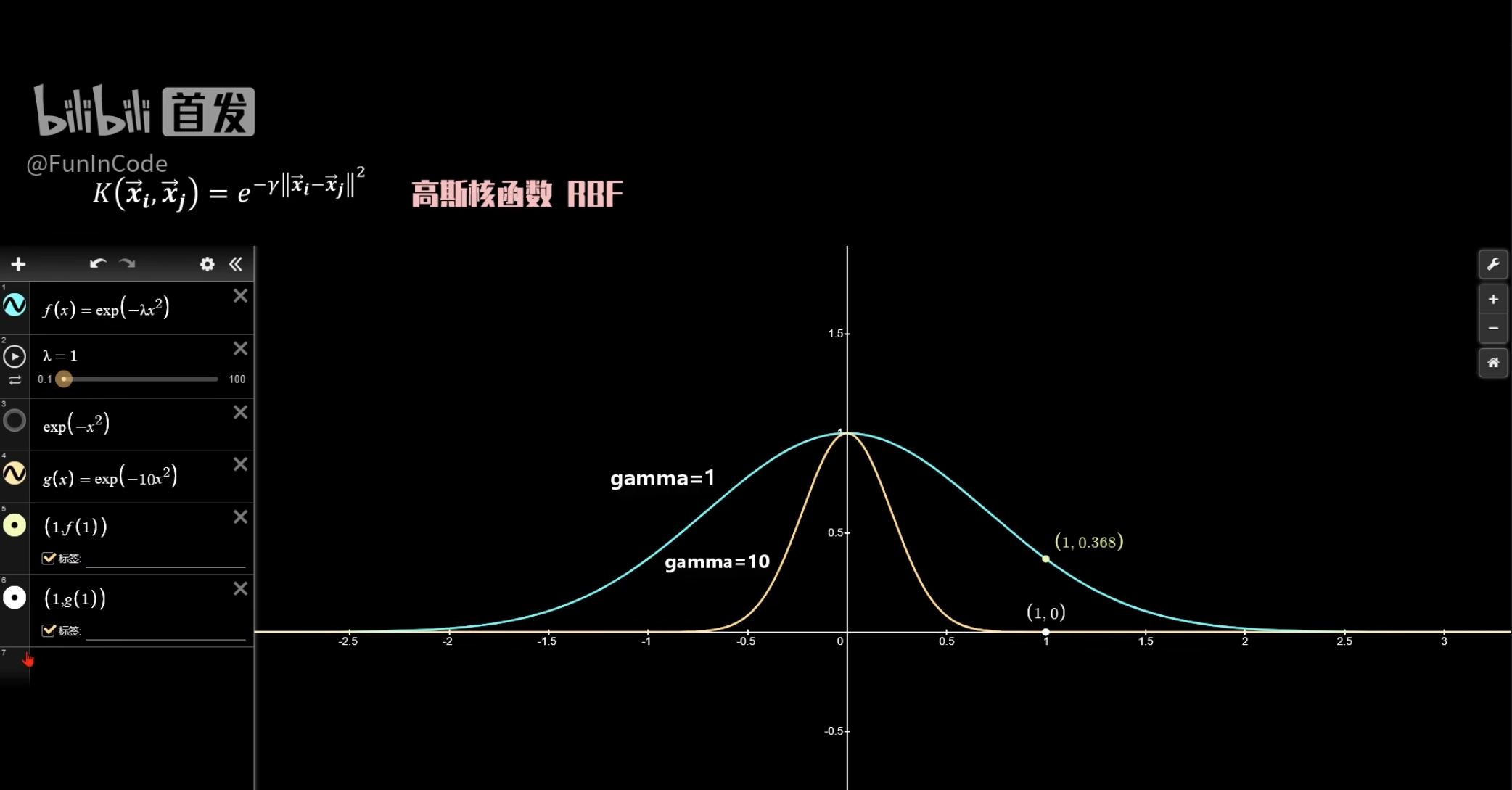
对于前面的高斯核函数,我们也要注意它的$ \gamma $值,当$ \gamma $值过大时,需要两个向量之间很近,它们的相似度才不会为$ 0 $,注意,核函数本身就是计算内积,因此可以体现二者的相似度。相似度高的自然容易被分到一起,因此当$ \gamma $值过大时,仅仅相邻很近的向量会被划分为相同的,因此很容易造成过拟合。同时$ \gamma $过小的后果也就是会造成过于容易划分。