强化学习
引入
在强化学习中,不同于之前的监督学习,例如对于一个直升飞机来讲,似乎我们很难人为的评断什么是好的,什么是坏的,我们更多的是通过奖励来对其行为进行调整。
和监督学习相比较,强化学习中的标签是后给出的,与无监督学习相比,强化学习中使用了标签。
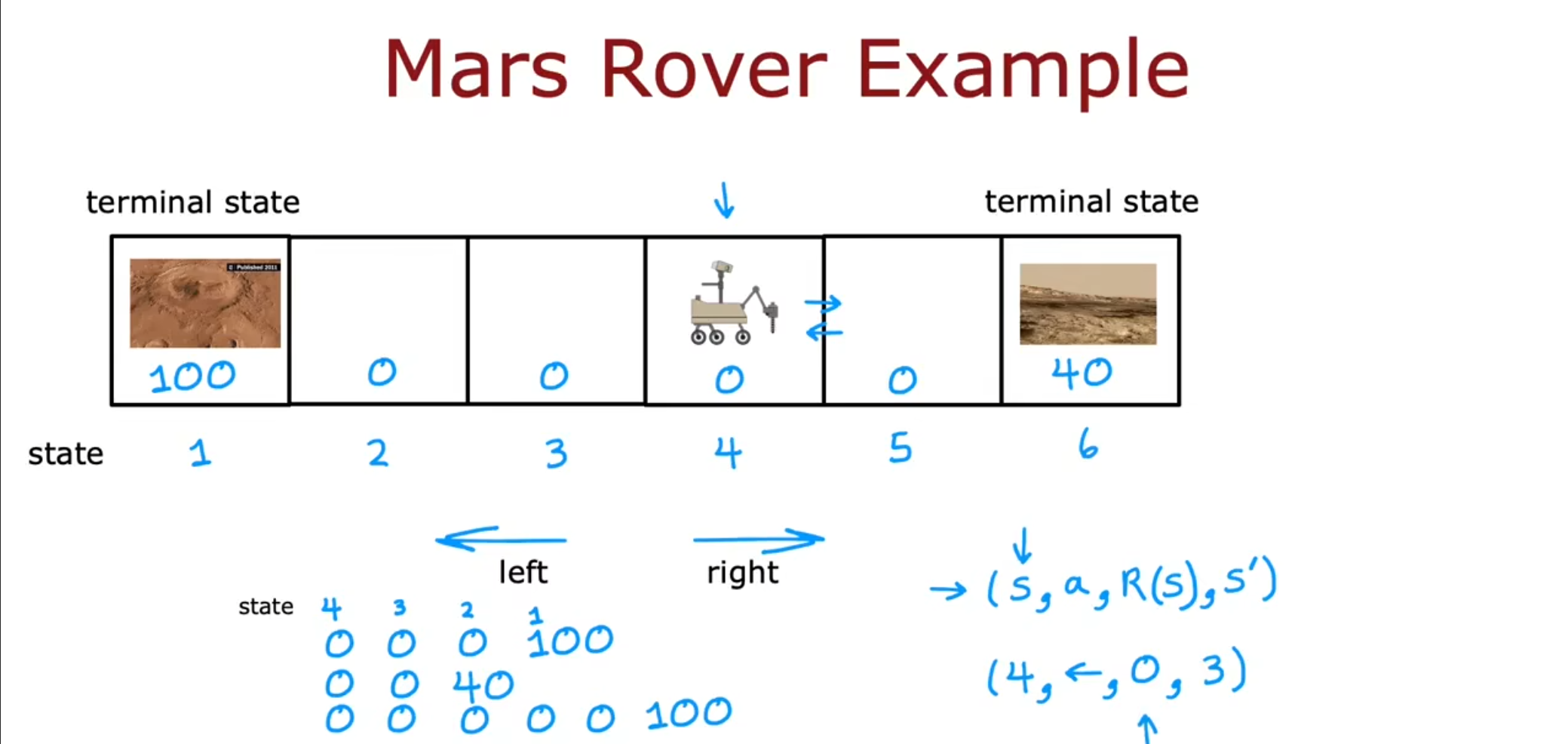
例如对于这个火星探测车,我们需要它拍摄到有价值的图片,也就是到达$ state1 $或$ state6 $,这样就可以得到奖励为$ 100 $或$ 40 $,假设我们现在处于$ 4 $这个状态,我们可以选择向左或者向右移动,最终到达奖励的位置。

刚才我们仅仅看到目的地的奖励,但是显然$ 100 $的距离却比$ 40 $要远,那么我们就需要把距离这个因素也计算进去。 因此我们引入了一个新的概念–折扣因子$ \gamma $,在这里我们采用$ \gamma=0.5 $的情况来进行评估。
$ Reward $奖励,表示每个时刻采取动作后得到的是即时奖励
$ Return $回报,表示在时刻采取某个动作后到游戏结束可以得到的总的奖励,即$ U_t=R_t+R_{t+1}+R_{t+2}\ldots $
“ 注意上面的$ U_t $公式中的$ reward $采用的是大写字母,因为它们表示的是随机变量,小写字母$ r_t $表示的是在时刻$ s_t $采取某个具体动作$ a_t $后得到的具体的奖励值。”
上面给的$ U_t $计算公式是从$ t $时刻开始未来每个时刻的奖励的累加,可以看到所有时刻的$ reward $都是相同权重的。但是这样设计有一个问题,就是假如我现在给你$ 100 $和$ 1 $年后才给你$ 100 $,这两个$ 100 $显然不应该赋予相同权重,所以你经常可以看到$ return $计算时会有一个参数$ \gamma $,得到的是$ discounted \quad return $,即$ U_t=R_t+\gamma R_{t+1}+\gamma^2R_{t+2}\ldots $
策略
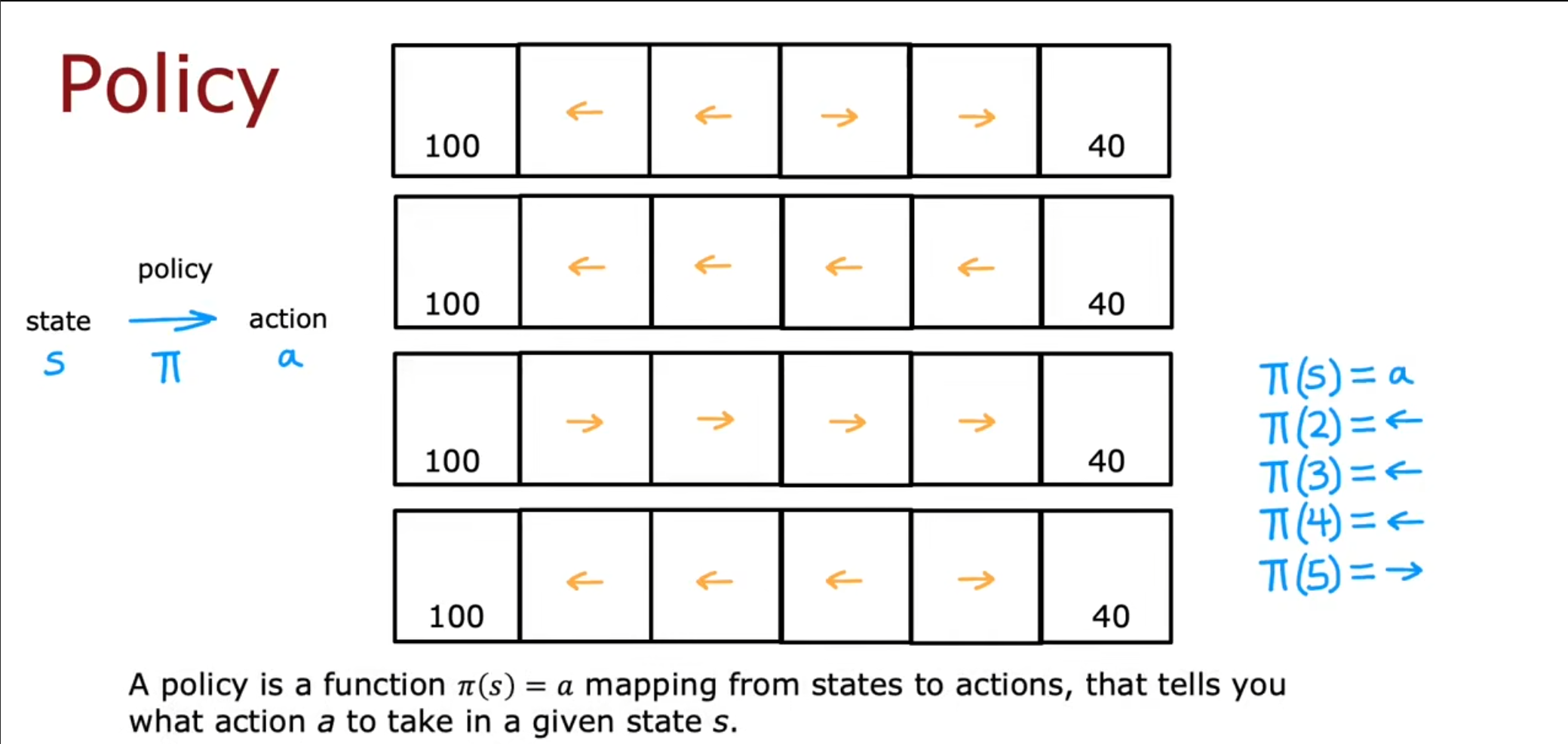
我们再介绍一个新的术语–策略$ \pi $,我们使用$ \pi{(s)}=a $表示在状态$ s $下采用决策$ a $,也就是表明了我们在状态$ s $下应该采用的决策。
马尔科夫决策过程
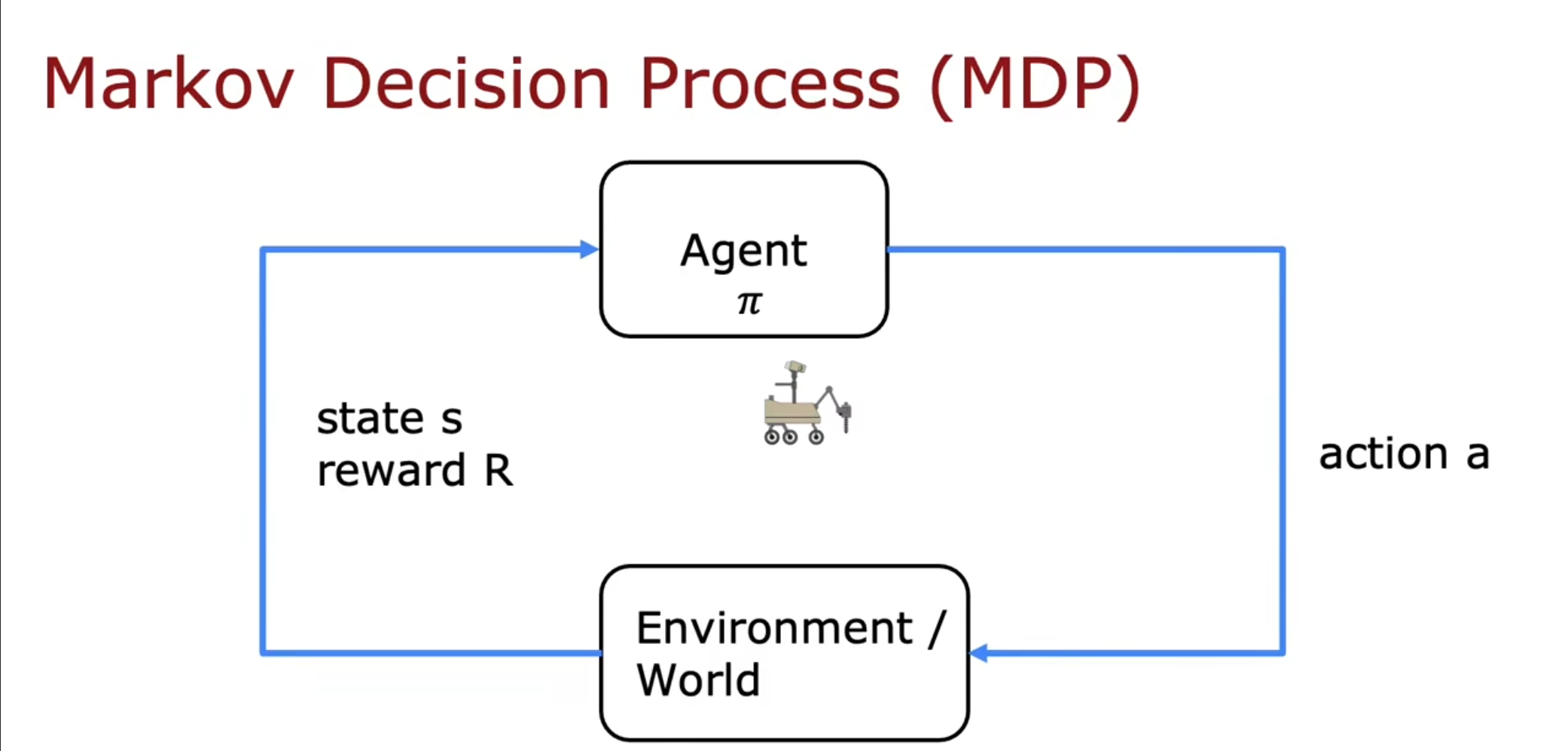
对用这种问题我们有一个经常使用的方法,称为马尔科夫决策过程,我们对于一个状态采取一个决策,然后基于这些决策发生的变化,得到新的状态和奖励。

我们再引入一个新的概念-动作价值函数,$ Q(s,a) $表示等于回报值,如果在状态$ s $下采用一次决策$ a $,然后接下来进行最优选择。
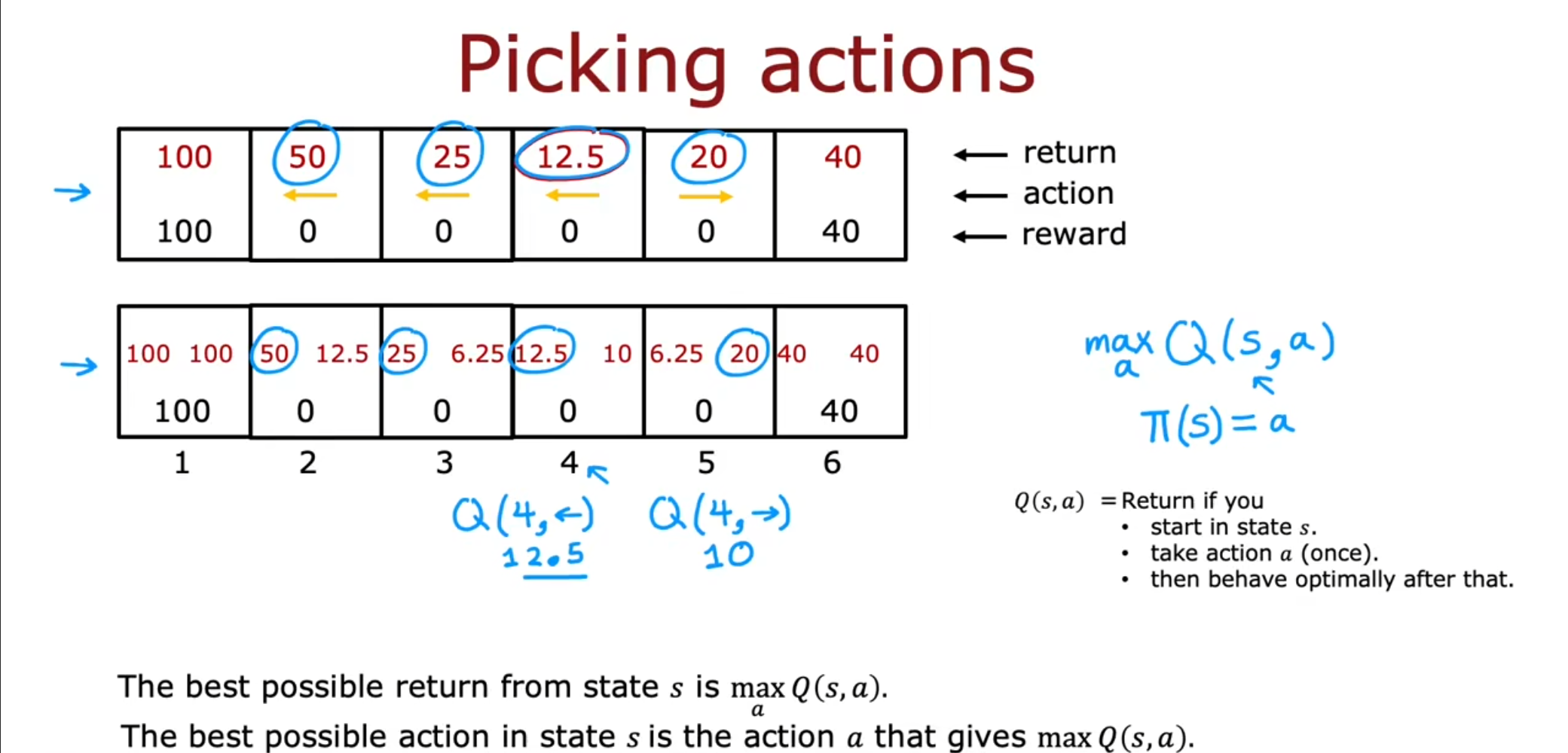
可以看到,最理想的收获值就是$ \max_{a}Q(s,a) $,在状态$ s $下最理想的决策就是可以使得$ Q $为最大值的决策。有的情况下这个函数也被写成$ Q^{*} $,实际上是一样的。
贝尔曼方程

上一节中提到了动作价值函数,那么如何计算,这就需要用到贝尔曼方程,即$ Q(s,a)=R(s)+\gamma \max_{a’}Q(s’,a’) $。

之前我们一直计算的都是最优的情况,但是实际上即使我们做出了最优的决策,但是仍存在可能事情不按照我们的决策进行,因此我们对于未来得到的回报就需要加上一个期望,表示在各种概率下的加权平均。
对于具体如何计算,可以参考这篇博客,用具体的例子展示了怎么使用贝尔曼方程列出等式并求解。
强化学习 1 —— 一文读懂马尔科夫决策过程(MDP)-CSDN博客
连续状态应用

我们之前讲的全部都是在离散的状态下进行的计算,但是在现实中很多东西都不是离散的,因此我们可以使用一个向量将这些数据作为输入进行计算,例如控制一个直升机,我们就需要有$ x,y,z $三个轴,偏移方向,角速度等。
Deep Q-Network
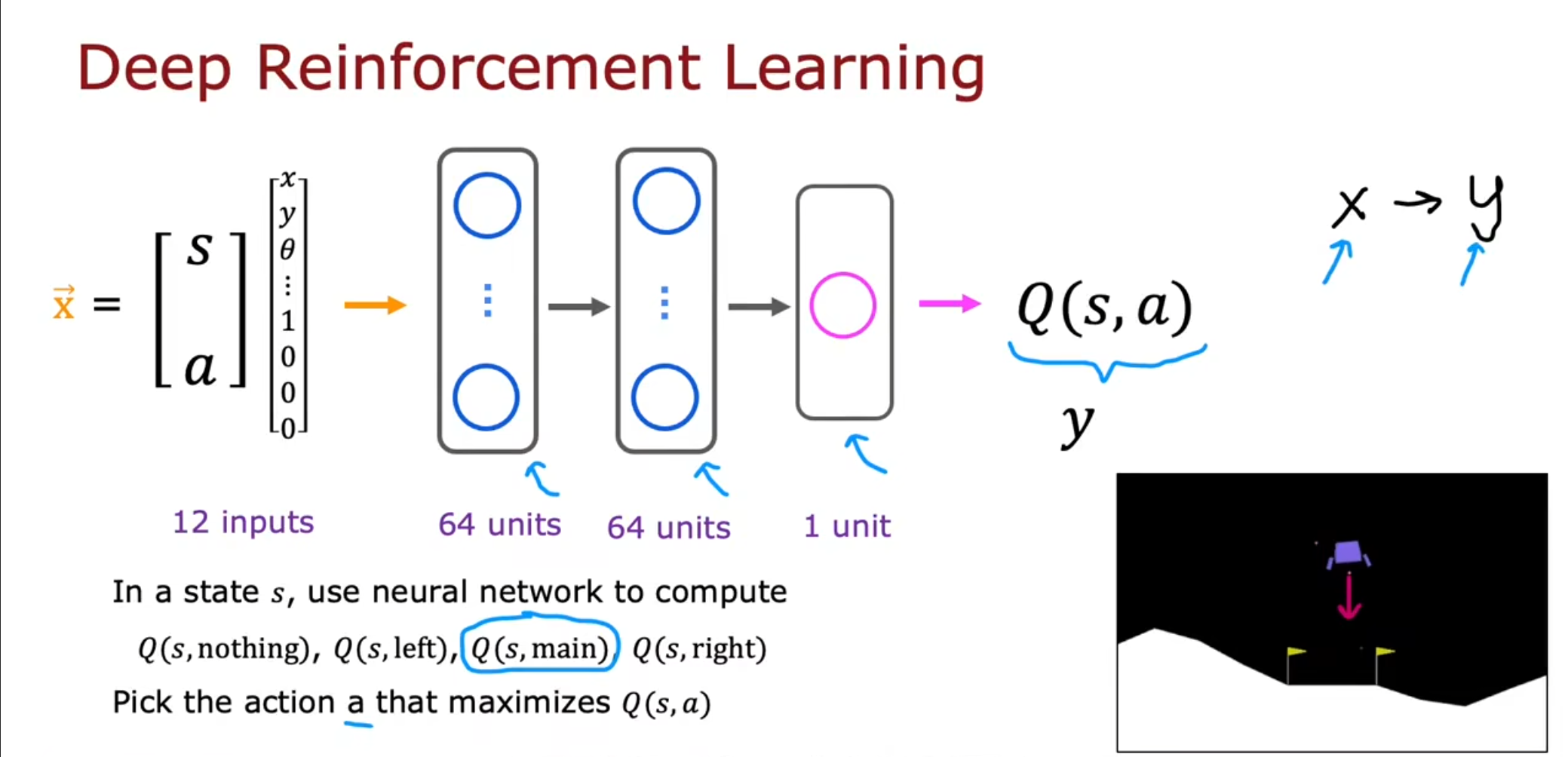
我们通过将深度学习的神经网络引入强化学习中,通过计算不同的$ Q(s,a) $得到最优的那个。

我们将状态值和决策设置为$ x $,将计算得到的$ y $设置为标签。

在这个算法中,首先随机初始化全部的$ Q(s,a) $函数,接着启动月球登陆器,收集信息,并将其存储在一个回放缓冲区中,接下来训练这个神经网络,我们得到一个新的$ Q_{new} $并使得这个数尽可能的靠近我们的计算值,最终将这个新的$ Q_{new} $设置为新的$ Q $。
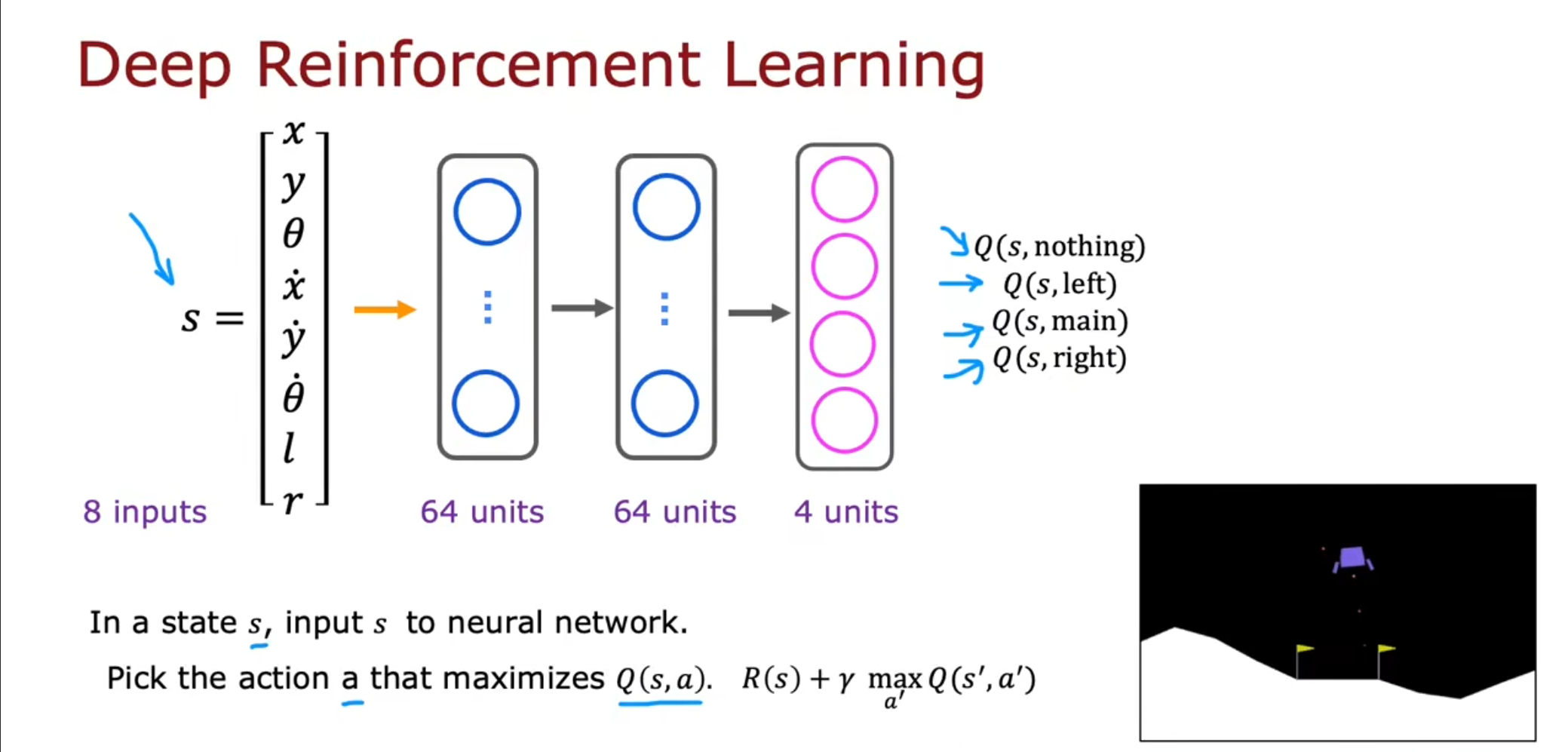
在之前的那个网络中我们需要对于每个决策都计算一次,但是我们可以改进这个神经网络的输出层,使得这个输出层可以一次计算四个值。
$ \epsilon $贪婪策略

由于之前的$ Q $值都是随机初始化的,因此我们选择最大值有的时候可能会很糟糕,我们引入了一个新的策略,使用一个超参数$ \epsilon $,使得这个算法可以在探索$ (exploration) $和利用$ (exploitation) $之间进行权衡。我们有$ \epsilon $的可能性不根据最大值选择而是进行不同的尝试。
小批量和软更新
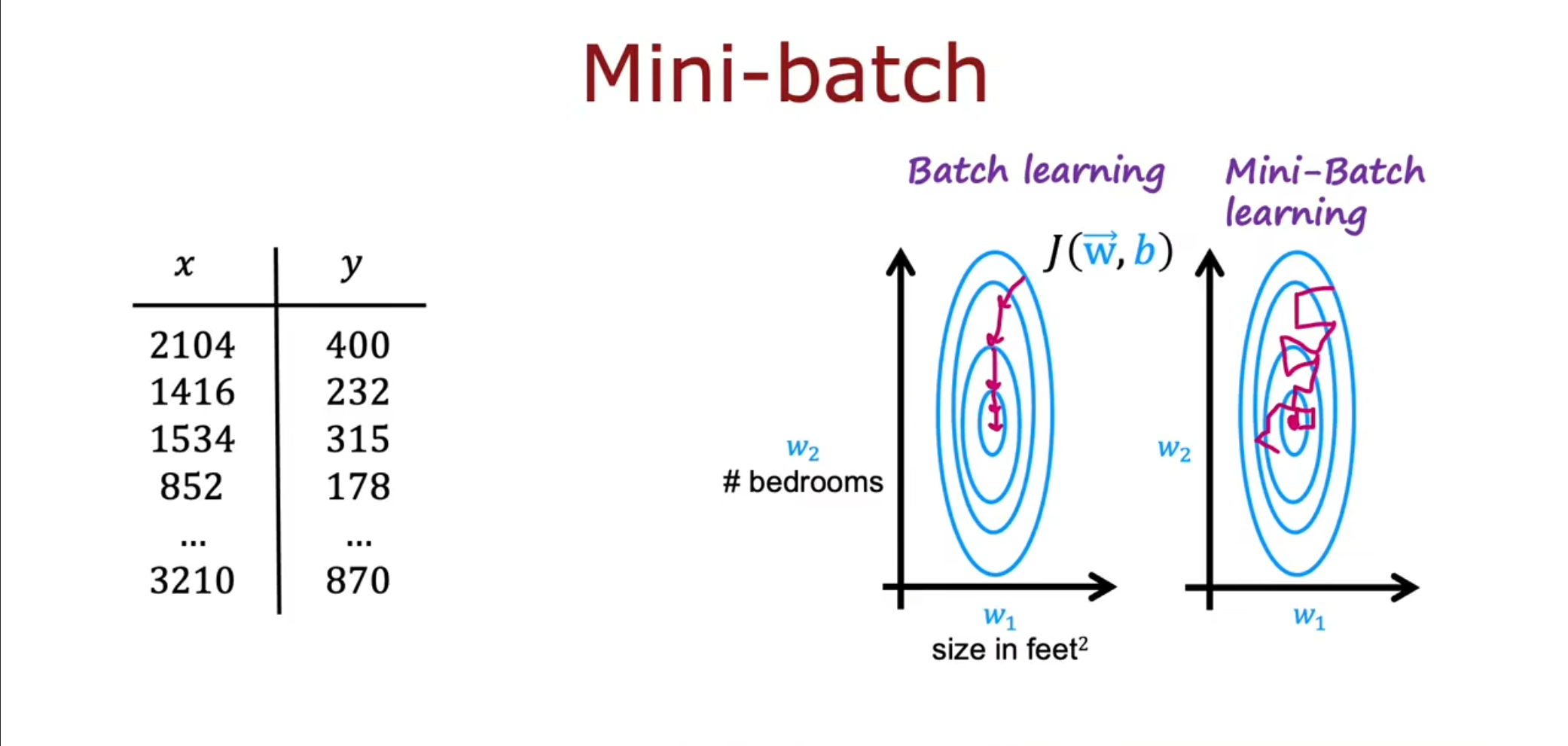
如果有很多的样本用例,可能是$ 10000000 $,如果一次更新那么在进行梯度下降运算的时候会很麻烦,因此,我们可以划分不同的$ mini-batch $,一次更新$ 32 $个,虽然这样看起来在趋于最小值的过程中显得十分曲折,但是最终也是会到达全局的最小值。

同时,在我们之前的更新中我们是直接将$ Q_{new} $设置为$ Q $,因此,如果我们训练的$ Q_{new} $并不是很好的话很可能使得$ Q $变得更糟糕,因此我们可以使用软更新,也就是例如上面的$ w,b $,使得新的值占的权重仅仅是一部分而不是全部。
马尔科夫推导-白板推导版
背景介绍

动态特性
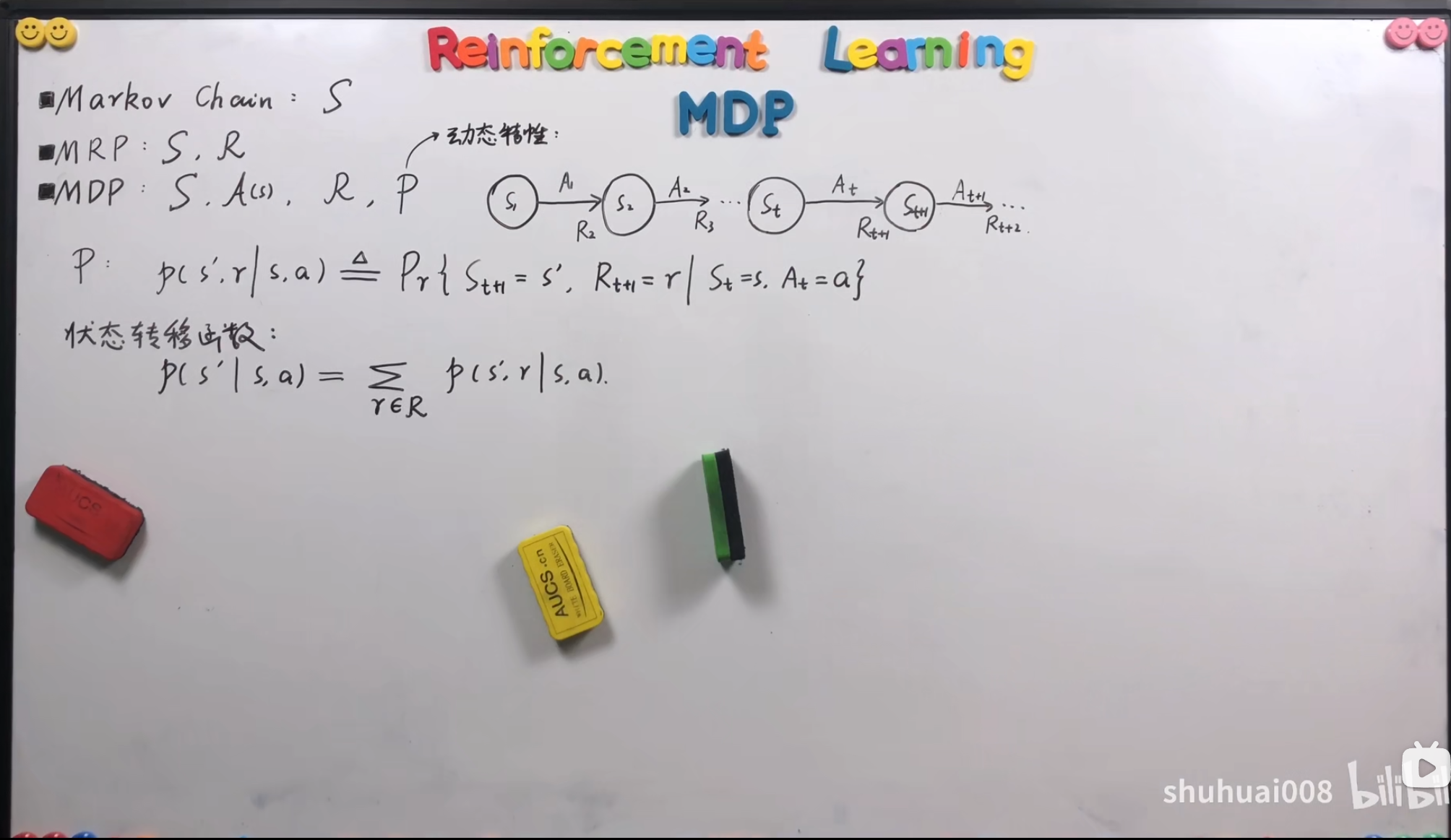
价值函数

贝尔曼期望方程

贝尔曼最优方程
