聚类算法
什么是聚类
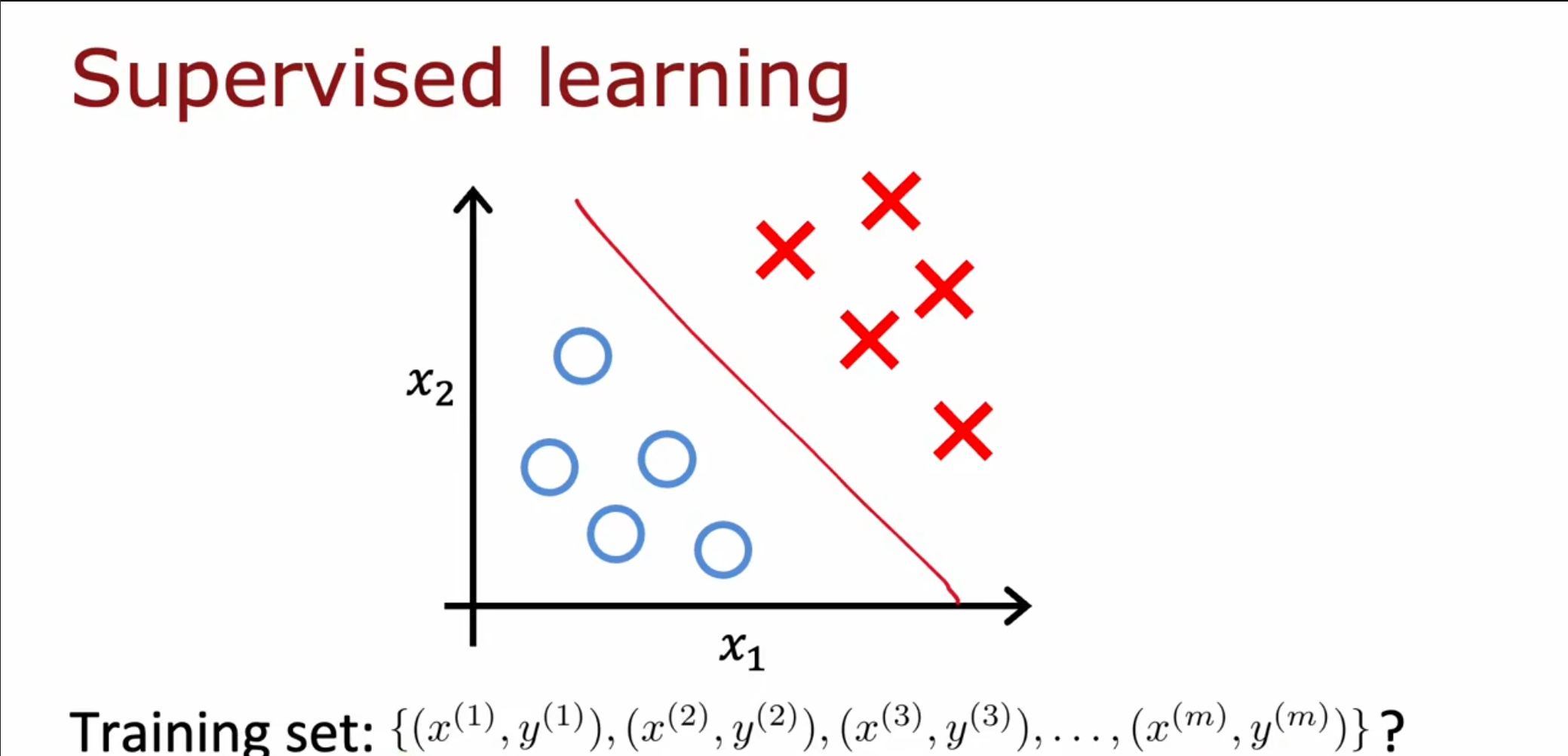
我们之前的训练数据都是一个特征对应一个标签,但是对于无监督学习来讲,仅需要数据本身,不需要添加标签。
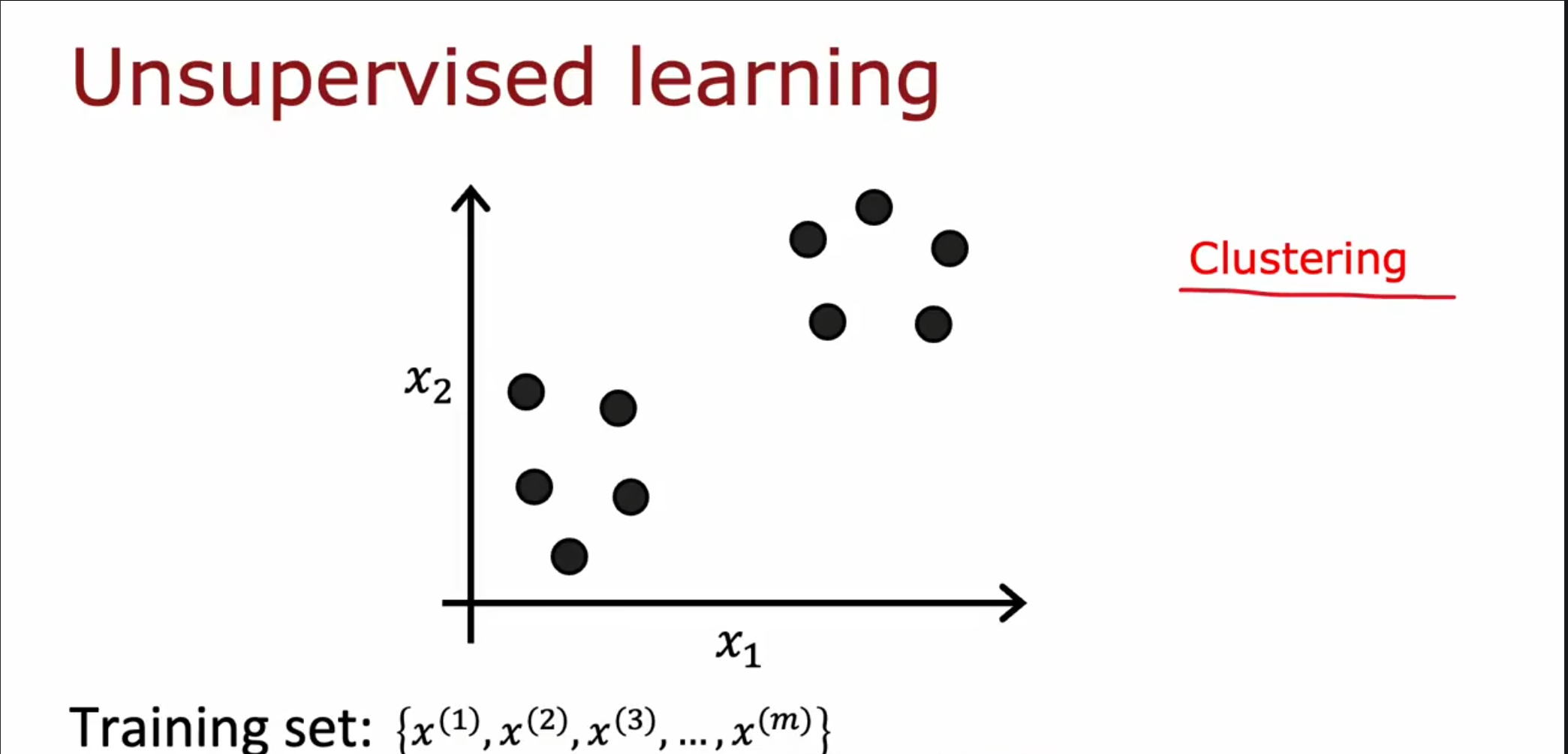
这种聚类算法可以被用于市场划分,新闻消息分组,$ DNA $检测,天文数据分析。
k-means的直观理解
对于$ k-means $可以分为两步进行。
第一步:
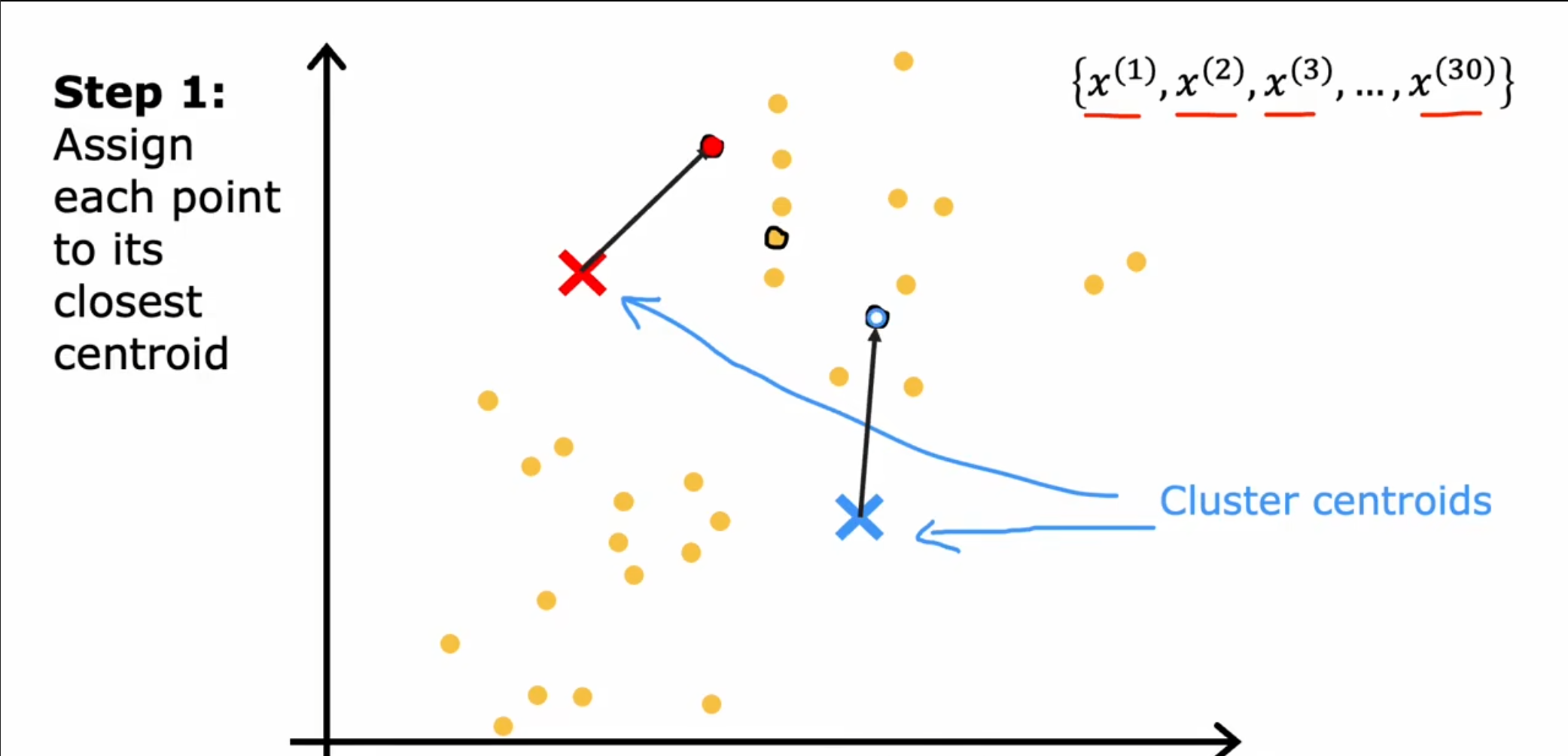
随机选择两个点作为簇质心,接着遍历每一个点,根据距离最近的质心,分别设置为不同的簇。
第二步:
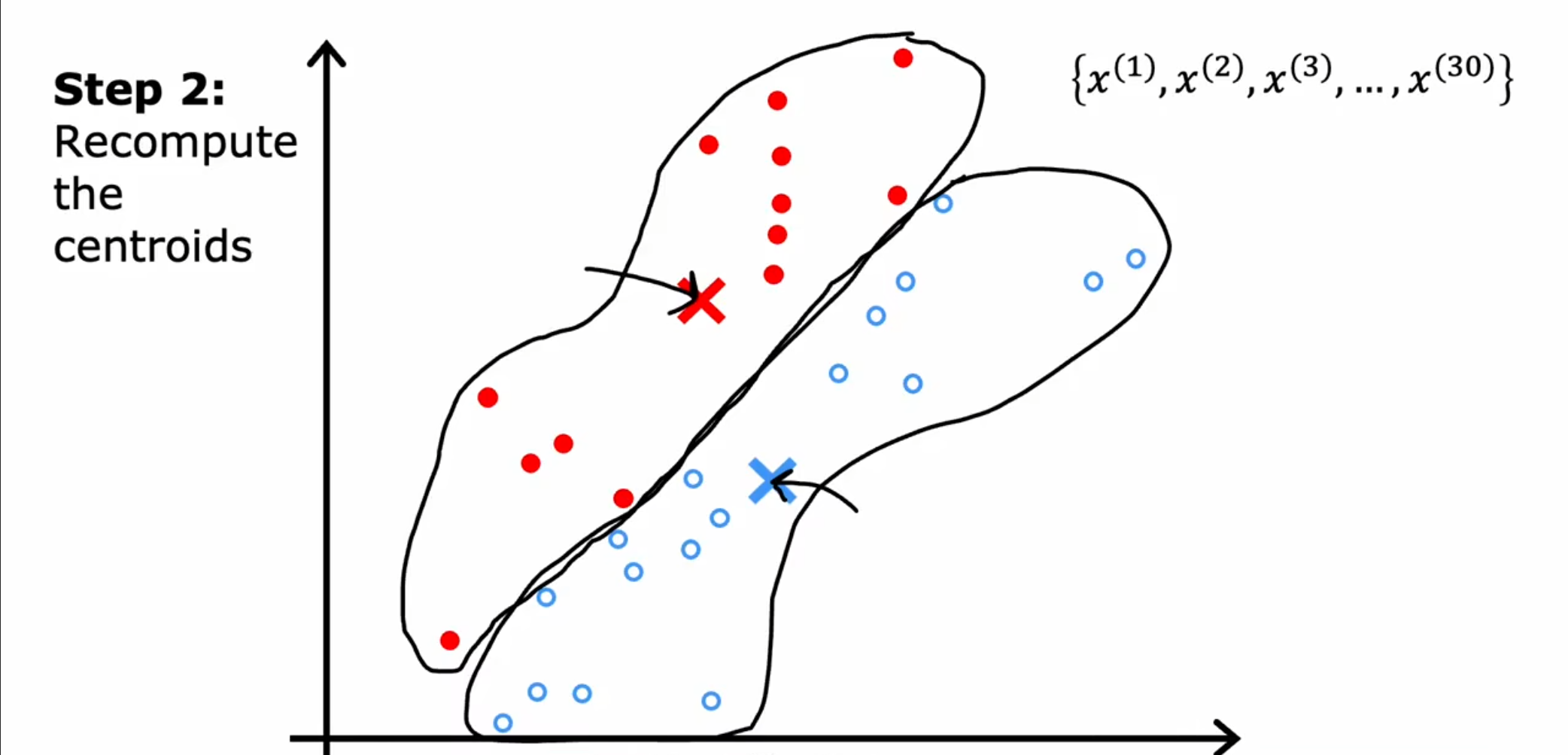
接着根据划分的点,计算他们的平均值,然后将之前的质心位置移动到新的平均值位置,重复第一步,最终直到计算平均值和质心的位置相同为止。
k-means算法

首先初始化$ k $个簇质心,接下来还是和之前的算法步骤相同,重复进行分配和移动质心的位置,最终使得质心保持不动。
需要注意的是一种特殊情况,如果出现了其中一个质心没有被分配到任何数据,那么也就无法进行调整,对于这种情况通常是将这个簇删除,但是如果一定要保持$ k $个簇,也可以将簇质心重新随机分配。
优化目标

我们首先定义几个变量
$ c^{(i)} $:当前点被分配的簇的下标
$ u_k $:簇的质心
$ u_{c^{(i)}} $:当前点被分配的簇的质心
根据这些变量我们可以得到这个失真代价函数:$ J\left(c^{(1)},…,c^{(m)},\mu_1,…,\mu_K\right)=\frac1m\sum_{i=1}^m\left|x^{(i)}-\mu_{c^{(i)}}\right|^2 $
为什么迭代后误差逐渐减小:
对于$ u_{c^{(i)}} $而言,求导后,当$ u_{c^{(i)}}=\frac{\sum{x_i}}{m} $时,代价函数最小,对应第二步;
对于$ x^{(i)} $而言,求导后,当$ x^{(i)}=c^{(i)} $时,代价函数最小,对应第一步。
因此$ k-means $迭代能使误差逐渐减少直到不变

在第一步中我们为每个点选择更近的那个簇质心,使得可以减少差值。
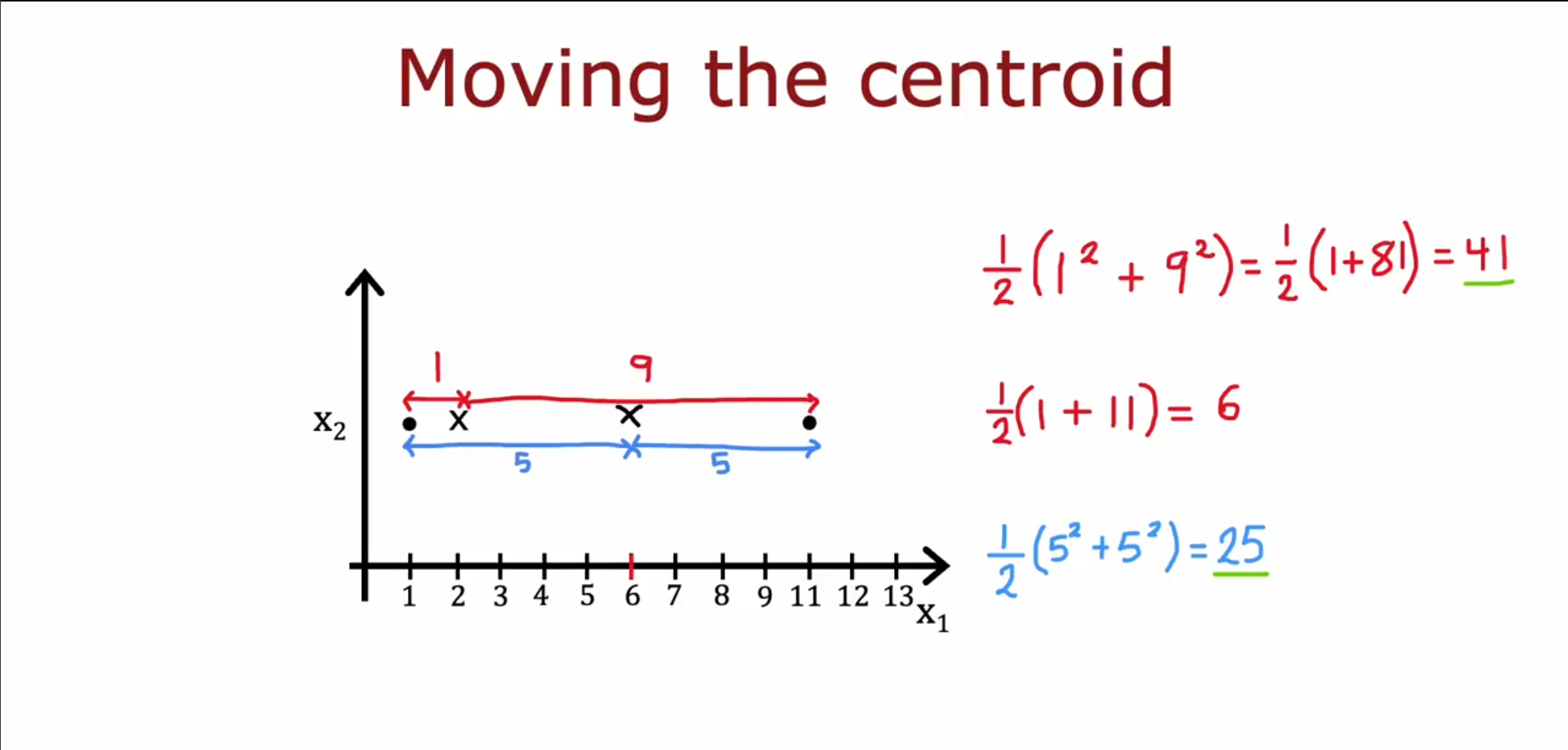
在第二步中我们将簇质心移动到中间点的位置,使得可以减少差值。
初始化k-means
- 随机初始化

由于我们之前的初始化点都是完全随机的,不同的初始化点对于算法的收敛速度有很大的影响,因此我们可以通过多次初始化得到一个最好的初始化结果。
第一步:选择$ k $个样本点作为初始化的簇质心。
第二步:运行$ k-means $算法,得到每个点分配的簇质心并计算代价函数。
第三步:通过多次循环,得到一个代价函数最小的值作为初始化的$ k-means $
- $ K-Means++ $
$ K-Means++ $的对于初始化质心的优化策略也很简单,如下:
$ a) $ 从输入的数据点集合中随机选择一个点作为第一个聚类中心$ μ_1 $
$ b) $ 对于数据集中的每一个点$ x_i $,计算它与已选择的聚类中心中最近$s$ 聚类中心的距离
$D(x_{i}) = argmin||x_{i}-\mu_{r}||_{2}^{2}$
$r = 1,2\ldots k_{selected}$
$ c) $ 选择一个新的数据点作为新的聚类中心,选择的原则是:$ D(x) $较大的点,被选取作为聚类中心的概率较大
$ d) $ 重复$ b $和$ c $直到选择出$ k $个聚类质心
$ e) $ 利用这$ k $个质心来作为初始化质心去运行标准的$ K-Means $算法
选择聚类数量
- 肘部法则
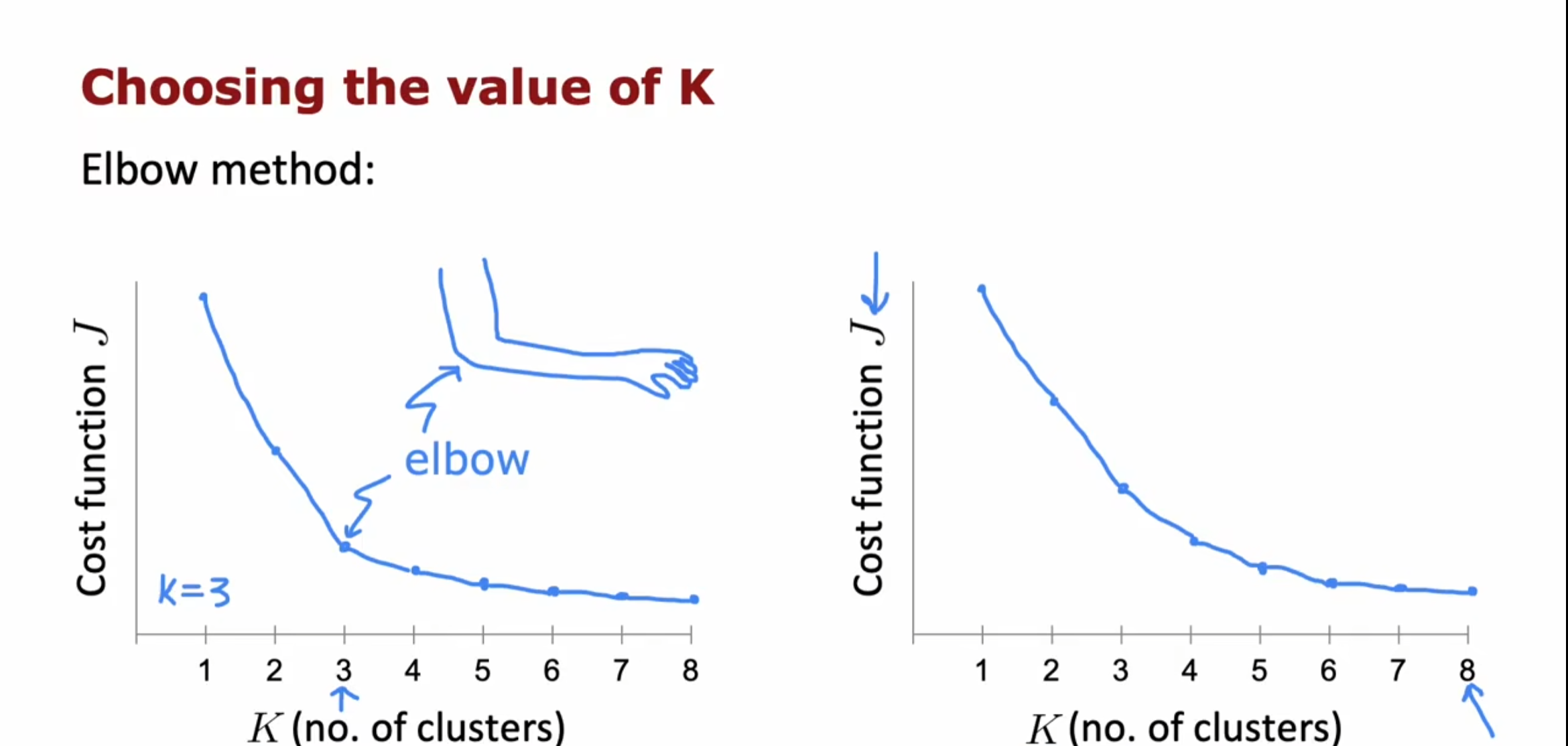
我们可以画出关于$ k $的代价函数图像,然后选择一个最明显的拐点,由于和人的肘部很像,因此也被称为肘部法则,但是这种方法并不是非常好用,因为像右侧的图像中代价函数的下降并不是非常陡峭无法直接判断合适的$ k $值。
- 轮廓系数法
轮廓系数$ (Silhouette Coefficient) $结合了聚类的凝聚度$ (Cohesion) $和分离度$ (Separation) $,我们希望簇内更加聚合,簇间更加分散,用于评估聚类的效果。该值处于$ -1\sim1 $之间,值越大,表示聚类效果越好。具体计算方法如下:
- 对于每个样本点$ i $,计算点$ i $与其同一个簇内的所有其他元素距离的平均值,记作$ a(i) $,用于量化簇内的凝聚度。
- 选取$ i $外的一个簇$ b $,计算$ i $与$ b $中所有点的平均距离,遍历所有其他簇,找到最近的这个平均距离,记作$ b(i) $,即为$ i $的邻居类,用于量化簇之间分离度。
- 对于样本点$ i $,轮廓系数$s(i)={\frac{(b(i)-a(i))}{max{a(i),b(i)}}}$
- 计算所有$ i $的轮廓系数,求出平均值即为当前聚类的整体轮廓系数,度量数据聚类的紧密程度
从上面的公式,不难发现若$ s(i) $小于$ 0 $,说明$ i $与其簇内元素的平均距离大于最近的其他簇,表示聚类效果不好。如果$ a(i) $趋于$ 0 $,或者$ b(i) $足够大,即$ a(i)<<b(i) $,那么$ s(i) $趋近与$ 1 $,说明聚类效果比较好。
- $ Calinski-Harabasz $法
$ s(k)=\frac{tr(B_k)}{tr(W_k)}\frac{m-k}{k-1} $
其中$ m $为训练集样本数,$ k $为类别数。$ B_k $为类别之间的协方差矩阵,$ W_k $为类别内部数据的协方差矩阵。$ tr $为矩阵的迹。
$$ B_k=\sum_{q=1}^kn_q(c_q-c_e)(c_q-c_e)^T
\newline W_k=\sum_{q=1}^k\sum_{x\in C_q}(x-c_q)(x-c_q)^T $$
其中$ c_q $表示类$ q $的中心点,$ c_e $表示数据集的中心点,$ n_q $表示类$ q $中的数据的数目,$ C_q $表示类$ q $的数据集合。
也就是说,类别内部数据的协方差越小越好,类别之间的协方差越大越好,这样的$ Calinski-Harabasz $分数会高。