模型选择与评估
模型评估

我们对于一个数据集进行划分,将其中$ 70% $的数据划分为训练集,将剩余$ 20% $的数据划分为测试集。

对于一个线性回归模型,我们得到了这三个公式,其中$ J(\vec{w},b) $是表示代价函数,$ J_{test}(\vec{w},b) $代表测试集的误差,$ J_{train}(\vec{w},b) $代表训练集的误差。
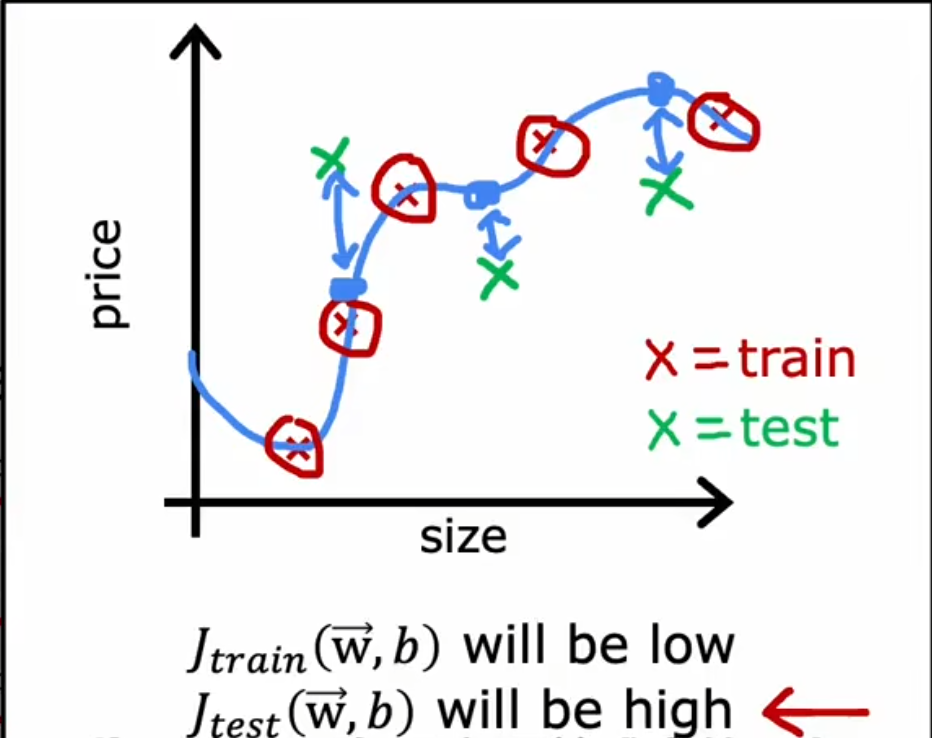
我们可以使用$ J_{test}(\vec{w},b) $和$ J_{train}(\vec{w},b) $来衡量该模型在测试集和训练集上的表现,显然对于这个过拟合的曲线,它在训练集的表现很好,但是在测试集上的表现很糟糕。
交叉验证

我们前面讲到将数据集划分为训练集和测试集,训练集用于确定$ w,b $,验证集用于选择模型,确定一个合适的超参数$ d $和判断是否过拟合。但是由于测试集已经多次参与到了数据的拟合中,因此最终得到的泛化误差是过于乐观的,可能小于实际的误差值。
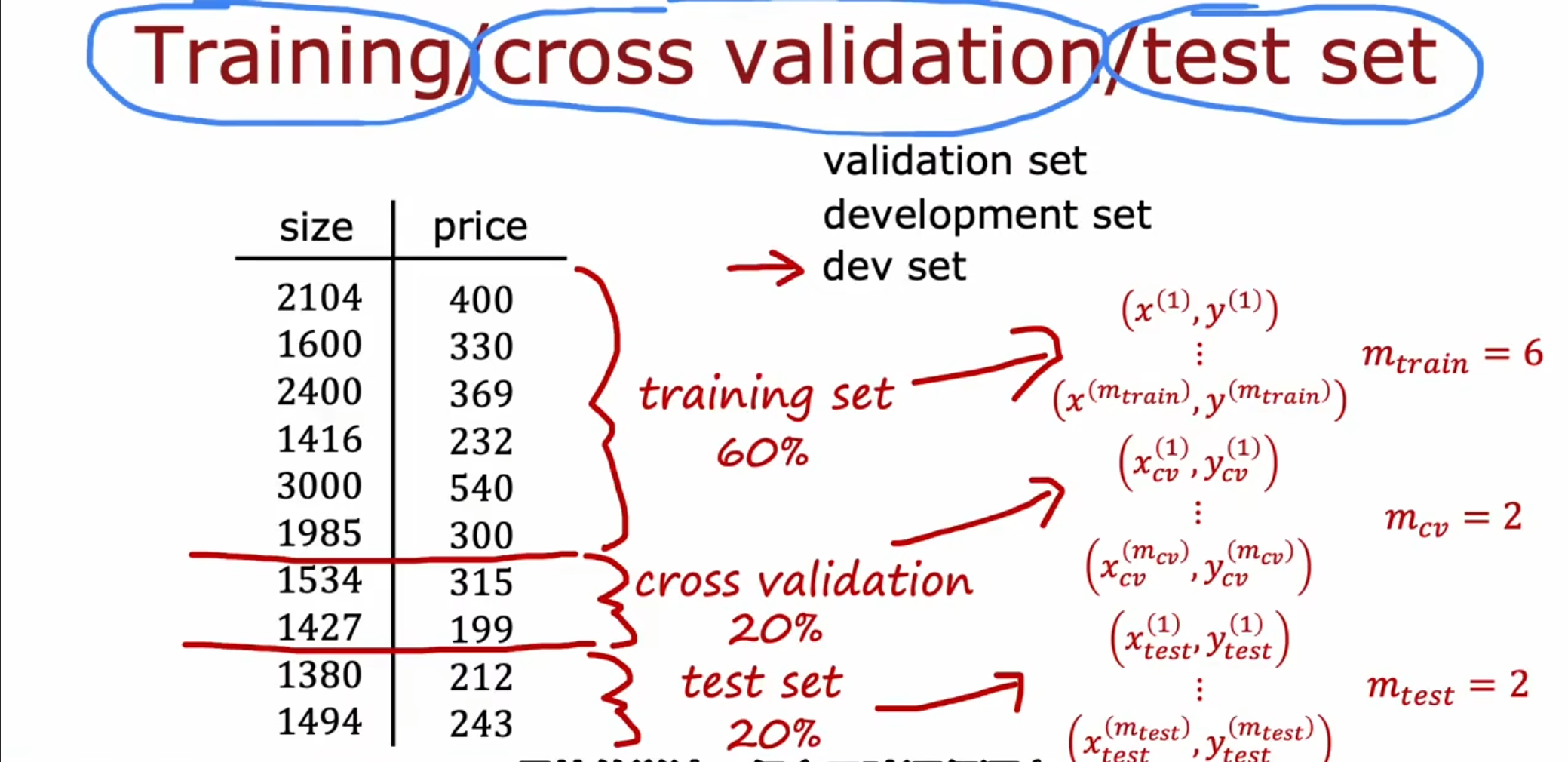
我们引入了一个新的概念-交叉验证集(也称为验证集,开发集),同时对于数据集进行重新划分,我们将其中的$ 60% $作为训练集,将剩下的$ 40% $分别各分一半作为验证集和测试集。
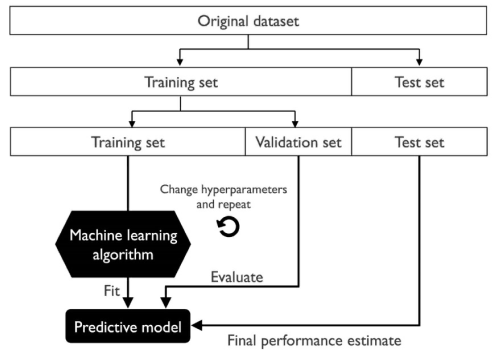
然后在训练集上训练模型,在验证集上选择模型,最后用测试集上的误差作为泛化误差的估计。我们可以在验证集上反复尝试不同的参数组合,当找到一组满意的参数后,最后在测试集上估计模型的泛化能力。

我们通过训练集训练数据,确定$ w,b $,同时使用验证集选择模型,确定超参数层数和隐藏的神经元个数以及是否过拟合,最终我们使用没有用过的测试集得到一个泛化误差。
偏差和方差
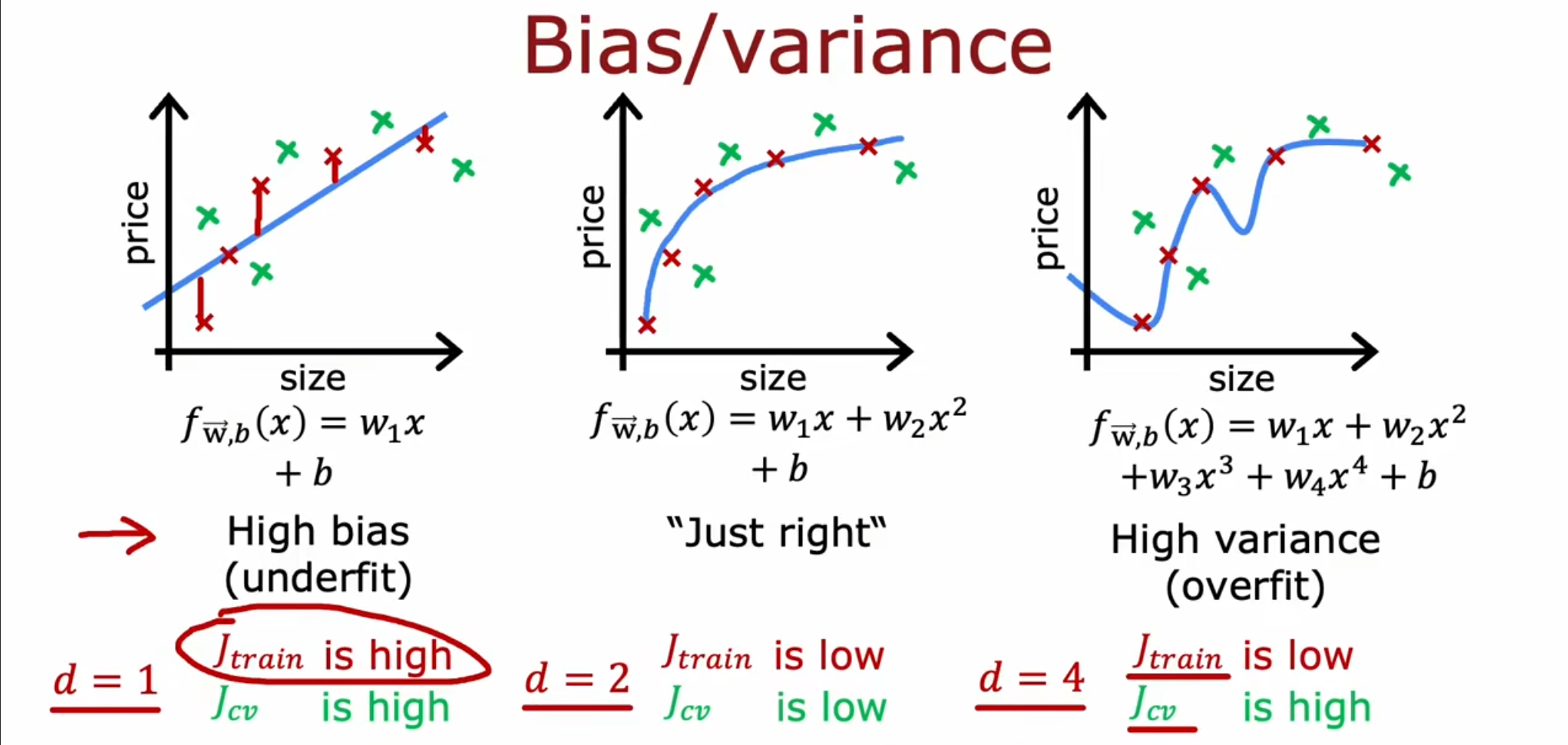
对于欠拟合,我们的模型在训练集和验证集上表现很糟糕,属于高偏差的情况。而对于过拟合,我们的模型在训练集上的表现很好,但是在验证集上的表现很糟糕,属于高方差。

当$ J_{train} $过高,同时$ J_{train}=J_{cv} $,那么就属于高偏差(欠拟合),当$ J_{cv}>>J_{train} $时,就属于高方差(过拟合)。当$ J_{train} $过高,同时$ J_{cv}>>J_{train} $,那么就是同时出现了高偏差和高方差,在程序中可能前半段的输入过拟合,后半段欠拟合,这种情况就会导致最终呈现高偏差和高方差。
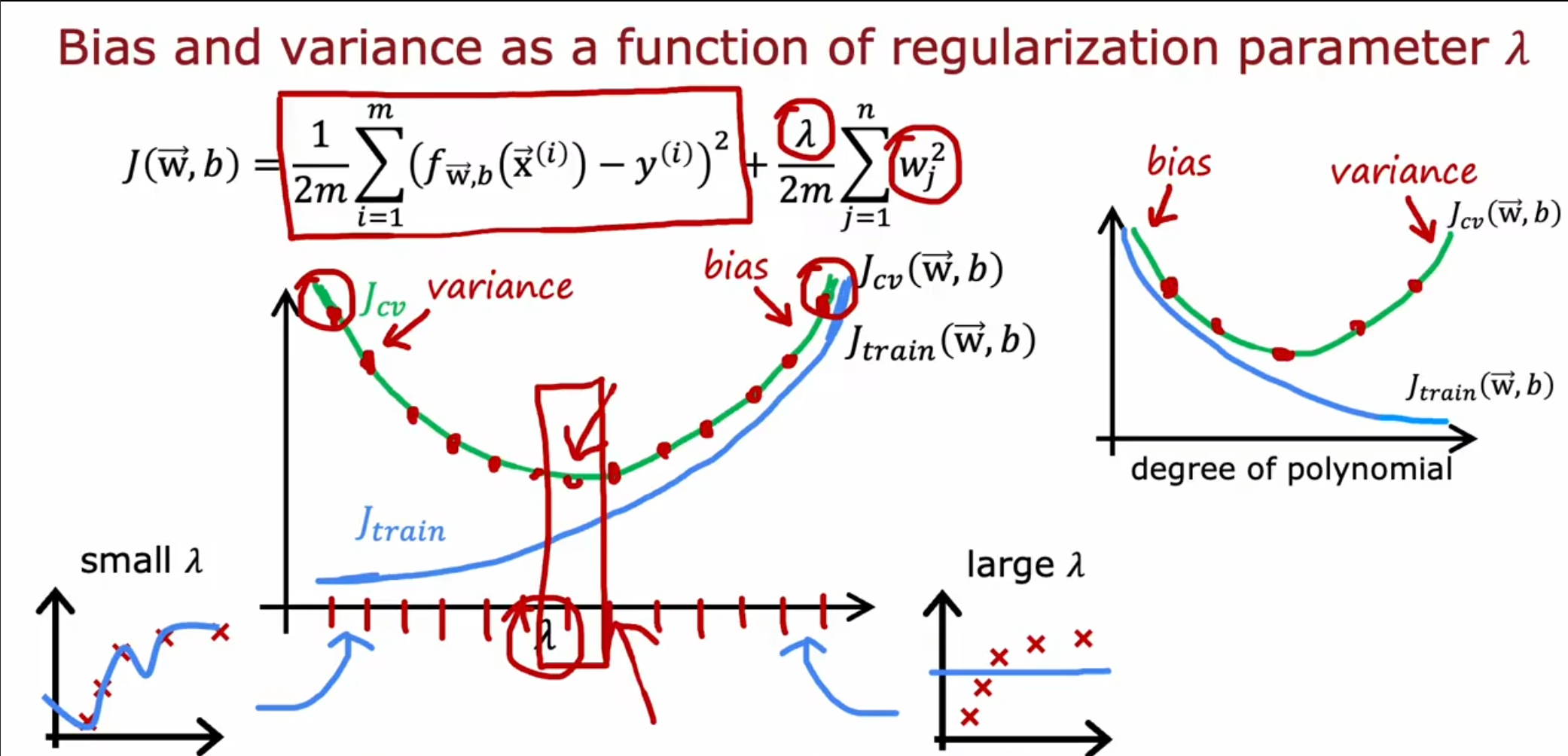
我们可以看到,正则化参数$ \lambda $的大小也会影响偏差和方差的值,同时与之前的多项式系数的图像成镜像关系。

我们在对训练的结果进行判断的时候要和基准线的表现相比较,将$ J_{train} $和基准线相比较,来判断是否高偏差,将$ J_{train} $和$ J_{cv} $相比较,判断是否高方差。
学习曲线
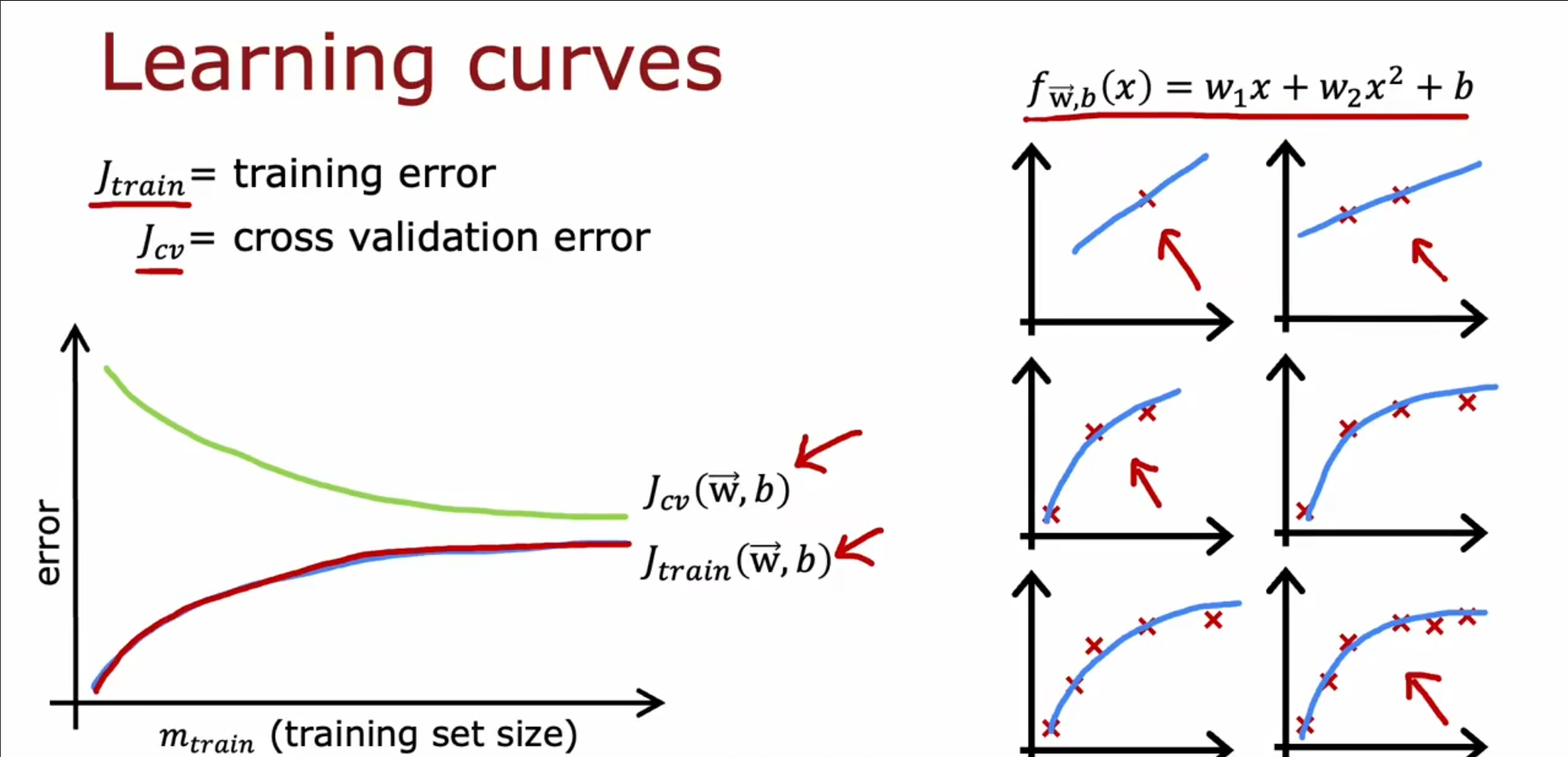
对于上图的学习曲线,$ J_{cv} $是从大到小,而$ J_{train} $是从小到大,当仅有一个时是没有误差的,随着训练集样本的增加,我们的曲线的偏离也逐渐增大。同时$ J_{cv} $的值在普遍情况下都是大于$ J_{train} $的值。
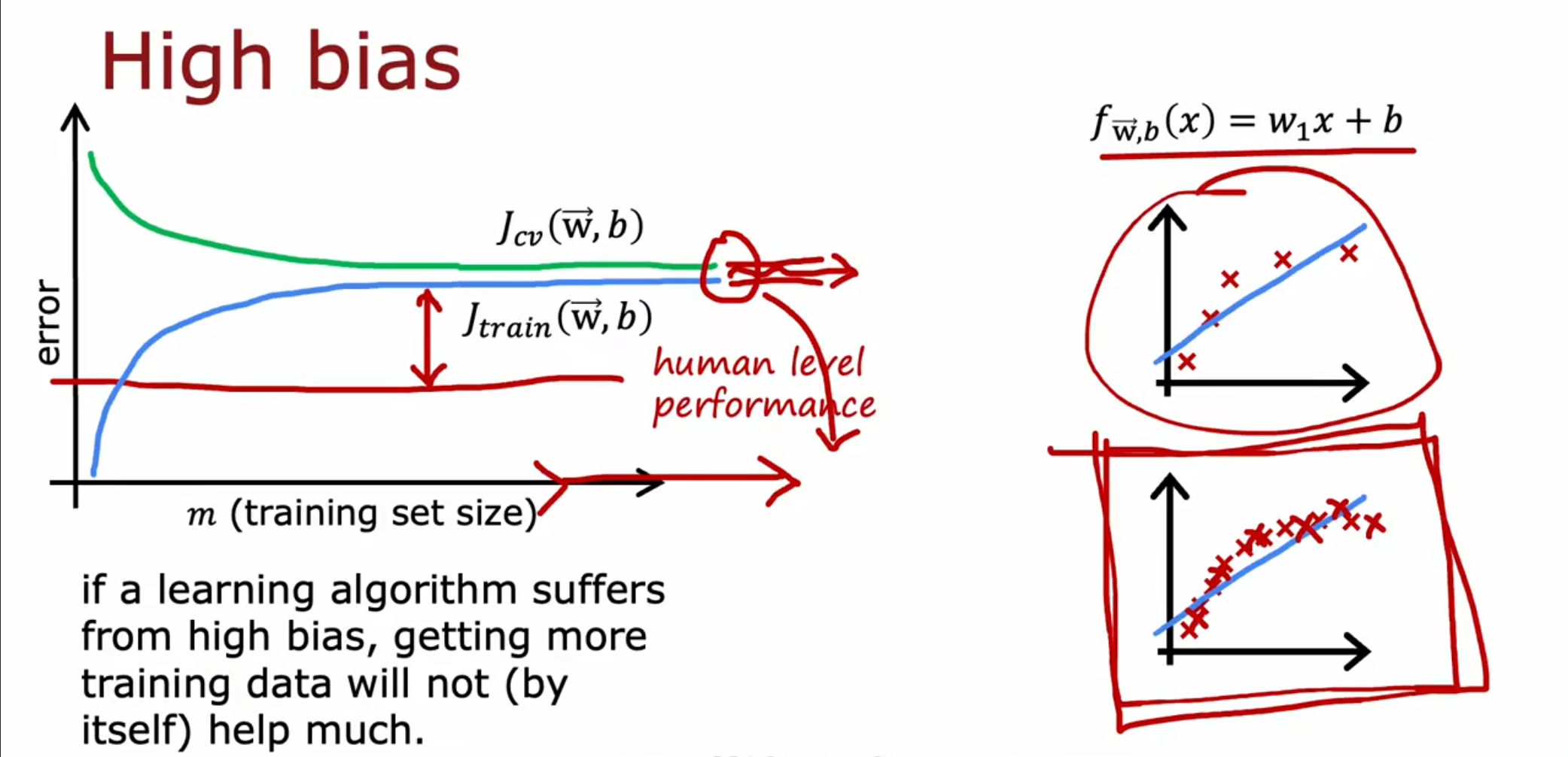
对于高偏差的情况,即使我们不断增大训练集的容量,但是我们的$ J_{cv} $和$ J_{train} $都无法降低到和人类的表现水平相同,仍远高于这个水平。
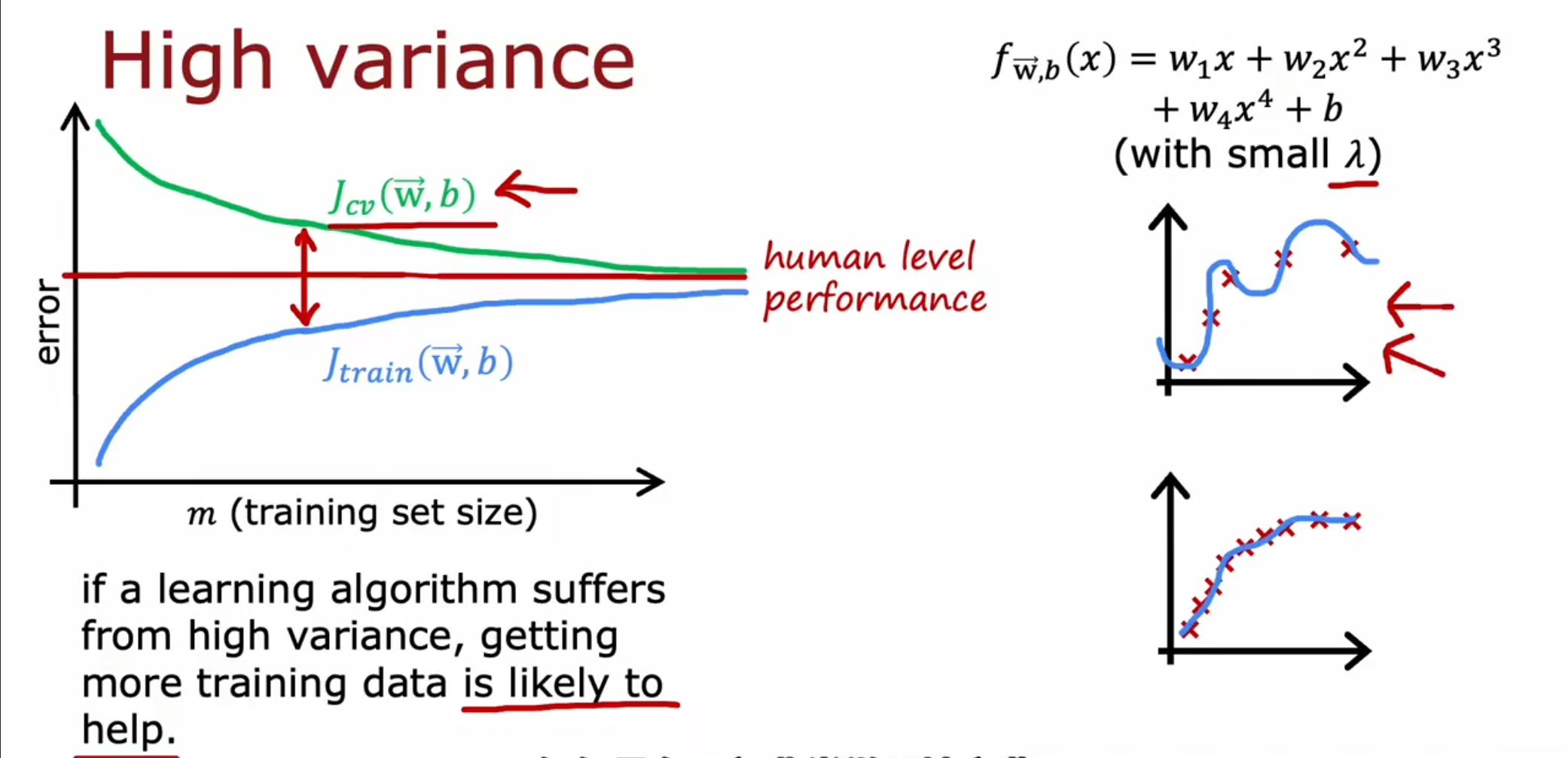
对于高方差的情况,随着我们对于训练集容量的提高,可以看到这将有利于我们的$ J_{cv} $和$ J_{train} $达到相接近的水平。

对于高偏差,我们可以使用增加特征,提高多项式的次数,减少正则化系数$ \lambda $等一系列方法。
对于高方差,我们可以增大训练集的容量,减少特征,增大正则化系数$ \lambda $等一系列方法。
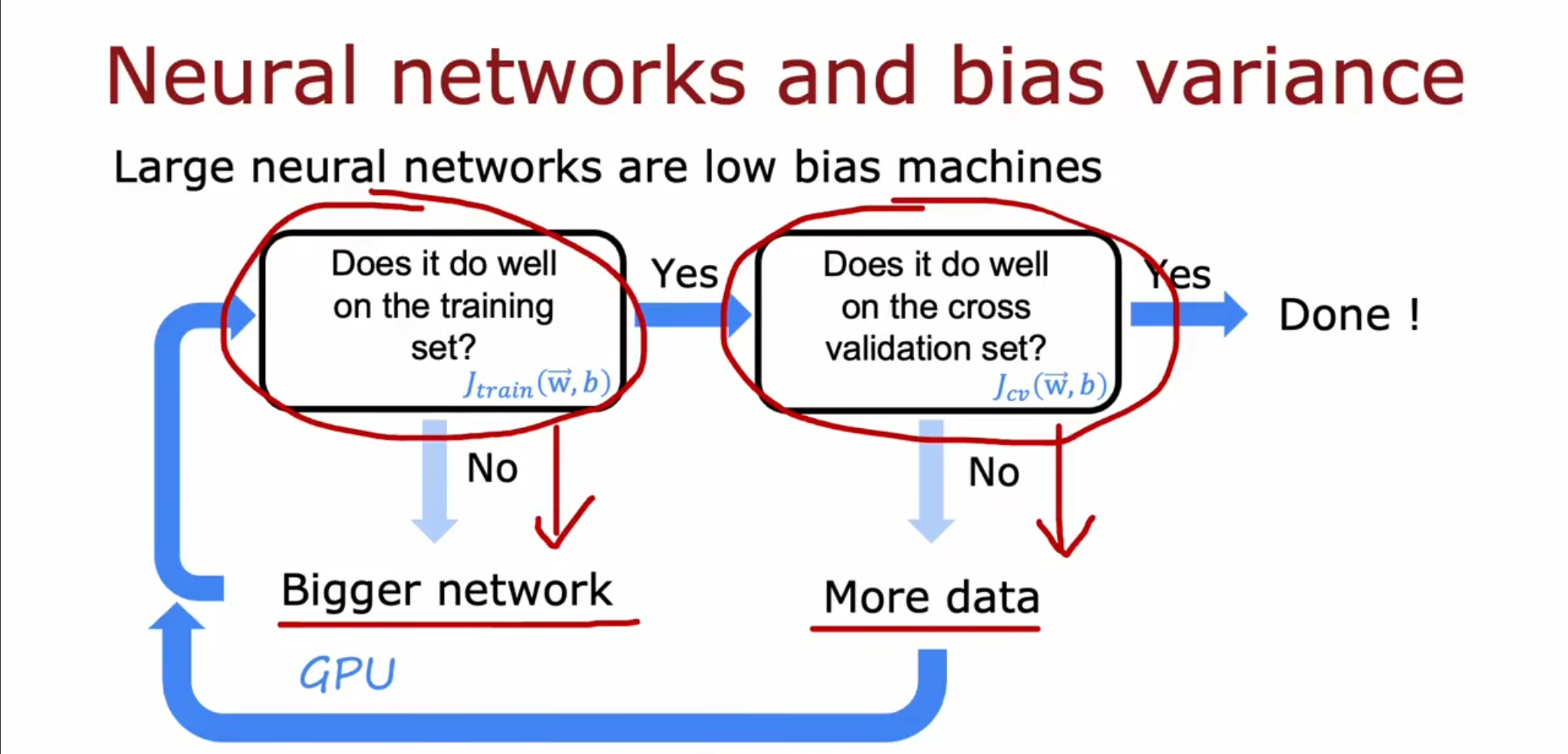
如果我们的模型太复杂就会导致高方差,如果太简单就会导致高偏差,为了在高偏差和高方差之间找到一个平衡点,我们可以按照这个顺序来进行调整。我们知道只要训练集的规模不算太大,那么在一个大型的神经网络上总是一个低偏差的状态,因此当我们的$ J_{train} $过大时就要增大神经网络的大小,直到可以在训练集上表现良好。接着如果在验证集上表现糟糕,那么就可以增大训练集的容量,同时回到第一步使得在训练集上表现良好,这样周而复始最终得到一个低偏差和低方差的结果。
当我们在扩大神经网络的时候只要选择了合适的正则化方法也不会导致方差的增大。
机器学习开发的流程
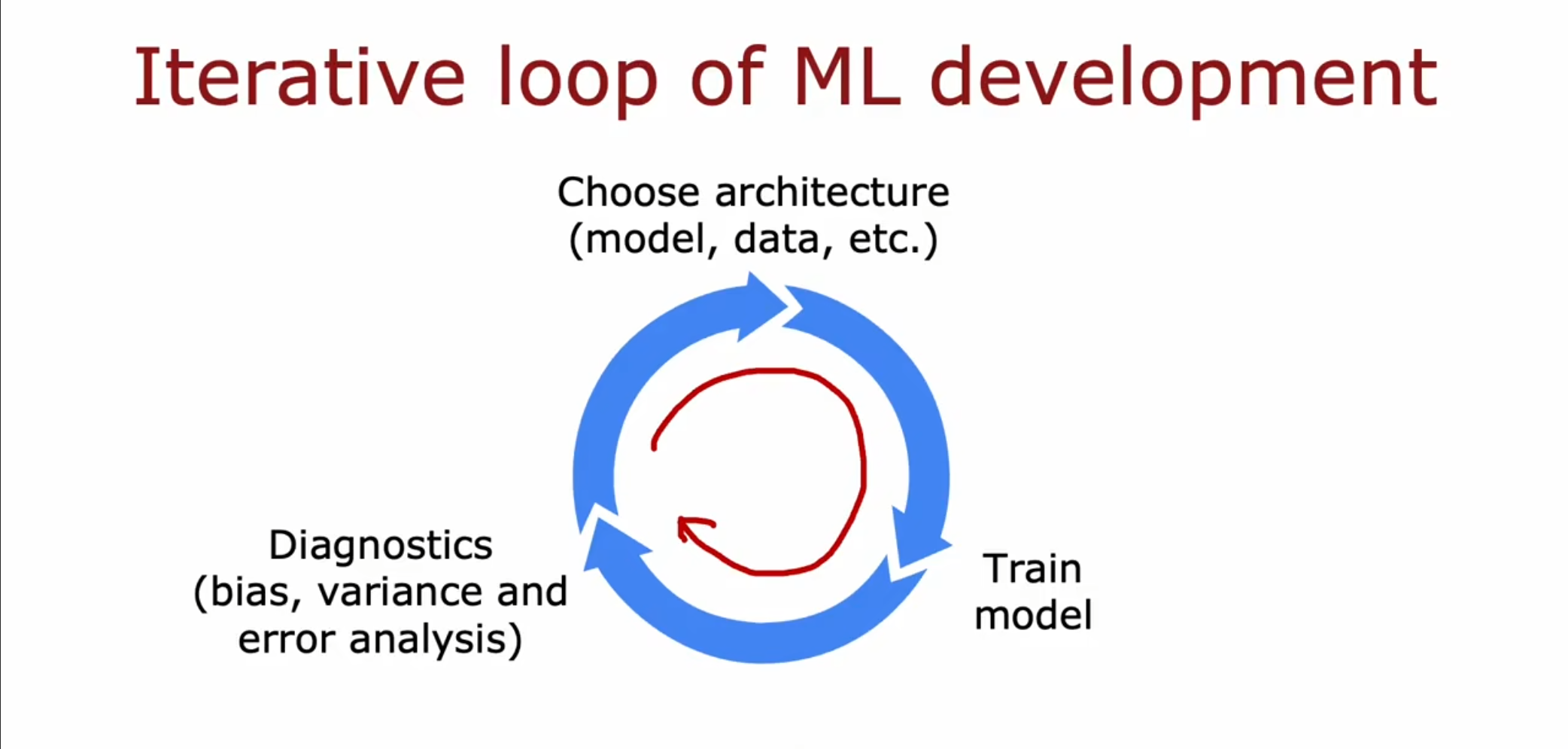
首先选择一个合适的模型,包含一些超参数和数据集的选择。接着进行模型的训练,根据训练的结果反向调整参数,通过偏差和方差大小的判断,重新对模型进行调整。
误差分析

我们对于验证集的$ 500 $个样例中的$ 100 $个被错误分类的样例进行分析。可以看到其中大部分都是由于医药邮件和窃取信息的邮件出现了错误分类,而对于故意的拼写错误很少,因此我们应该将中重点放在出现错误最多的地方。
数据增强

对于图像识别问题,我们可以通过将原本数据集进行扭曲和调整对比度形成新的数据。对于语音识别功能,我们可以添加一些噪音。但是如果添加一些完全随机或者没有意义的噪音对于数据的训练帮助不大。
迁移学习
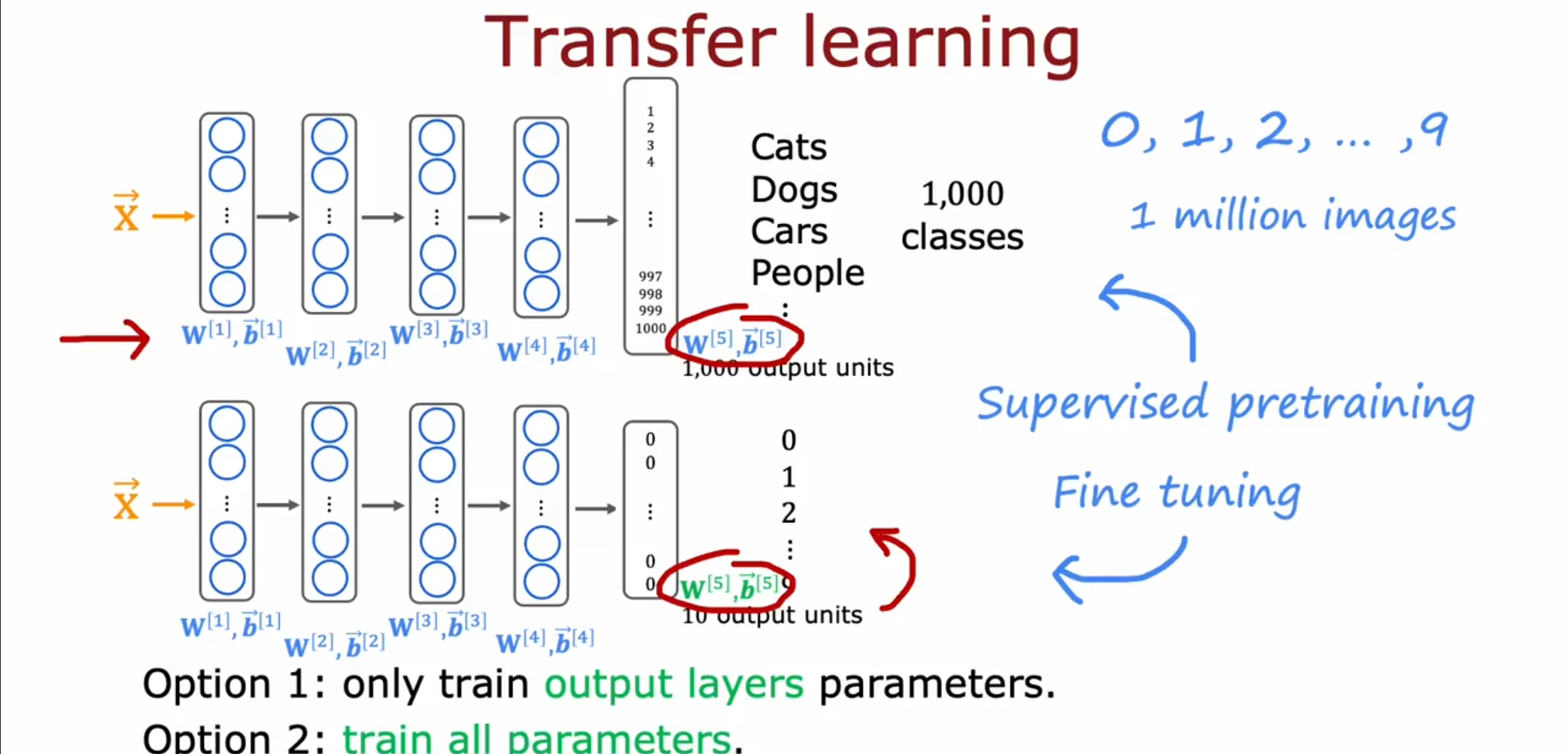
对于一些训练数据不够的情况,我们可以使用网上已经训练完成的模型,这被称为预训练模型。接着我们可以使用预先训练好的模型的参数作为初识参数,在训练的过程中进行调整,这个过程就被称为微调。
对于数据量不足的情况,我们可以选择仅训练输出层,根据自己的训练集对输出层函数进行调整。
对于数据量足够的情况,我们可以选择从头开始训练全部的参数。
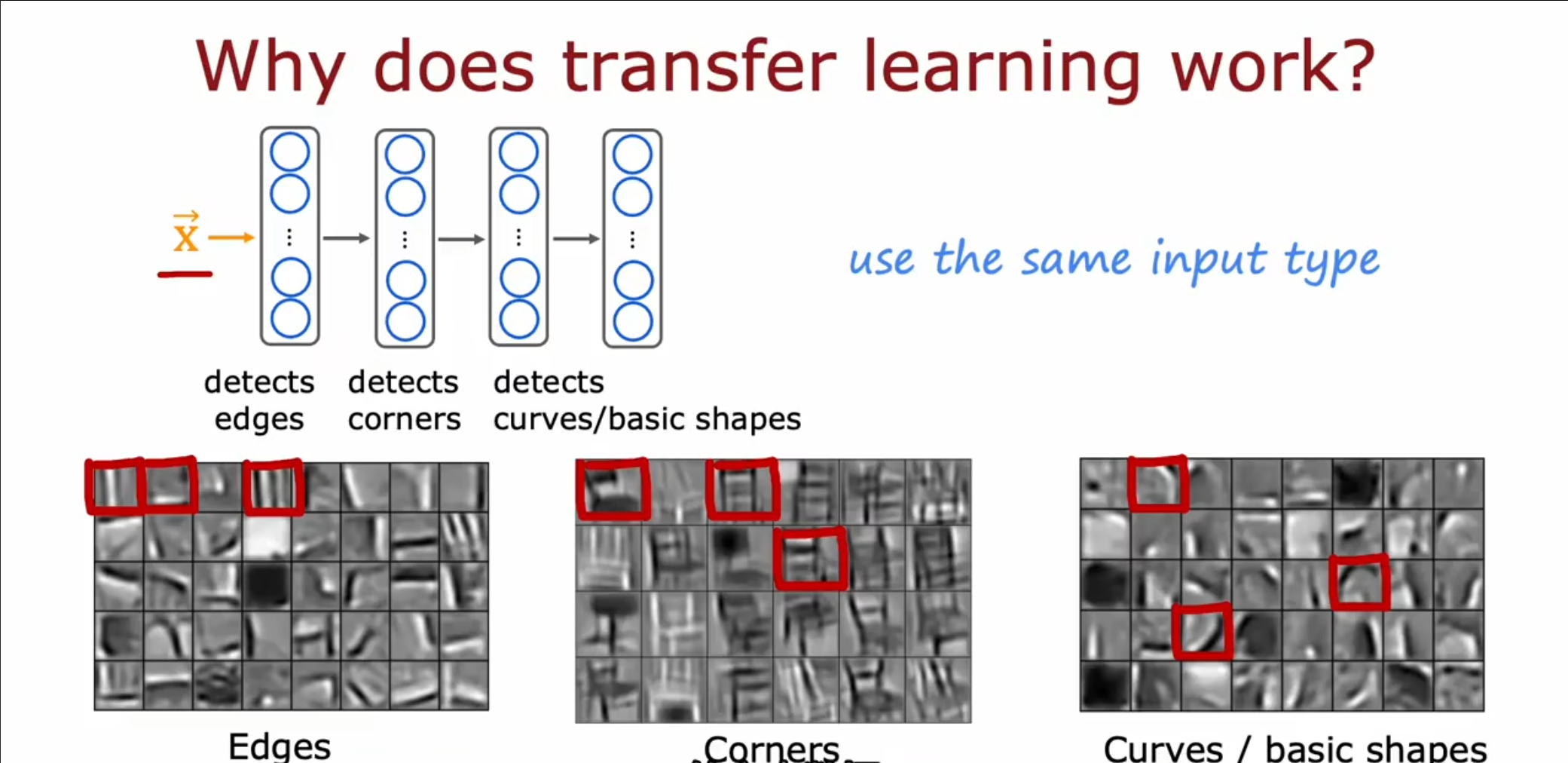
对于迁移学习的可行性,我们参照这个四层的神经网络可以看到,第一个隐藏层是在提取一些微小的边的特征。第二层是在提取一些角落特征,第三层是在提取一些曲线特征。因此我们可以看到对于图像识别问题,前几层所提取的信息,无论是对于车辆识别还是数字识别来讲,都是类似的,我们可以仅调整最后一层的输出,使得符合我们自己训练的数据集。
同时需要注意的是,我们的输入的类型都要是相同的,对于图形处理的预处理模型我们不可以拿来进行语言模型的训练。
机器学习项目的完整流程
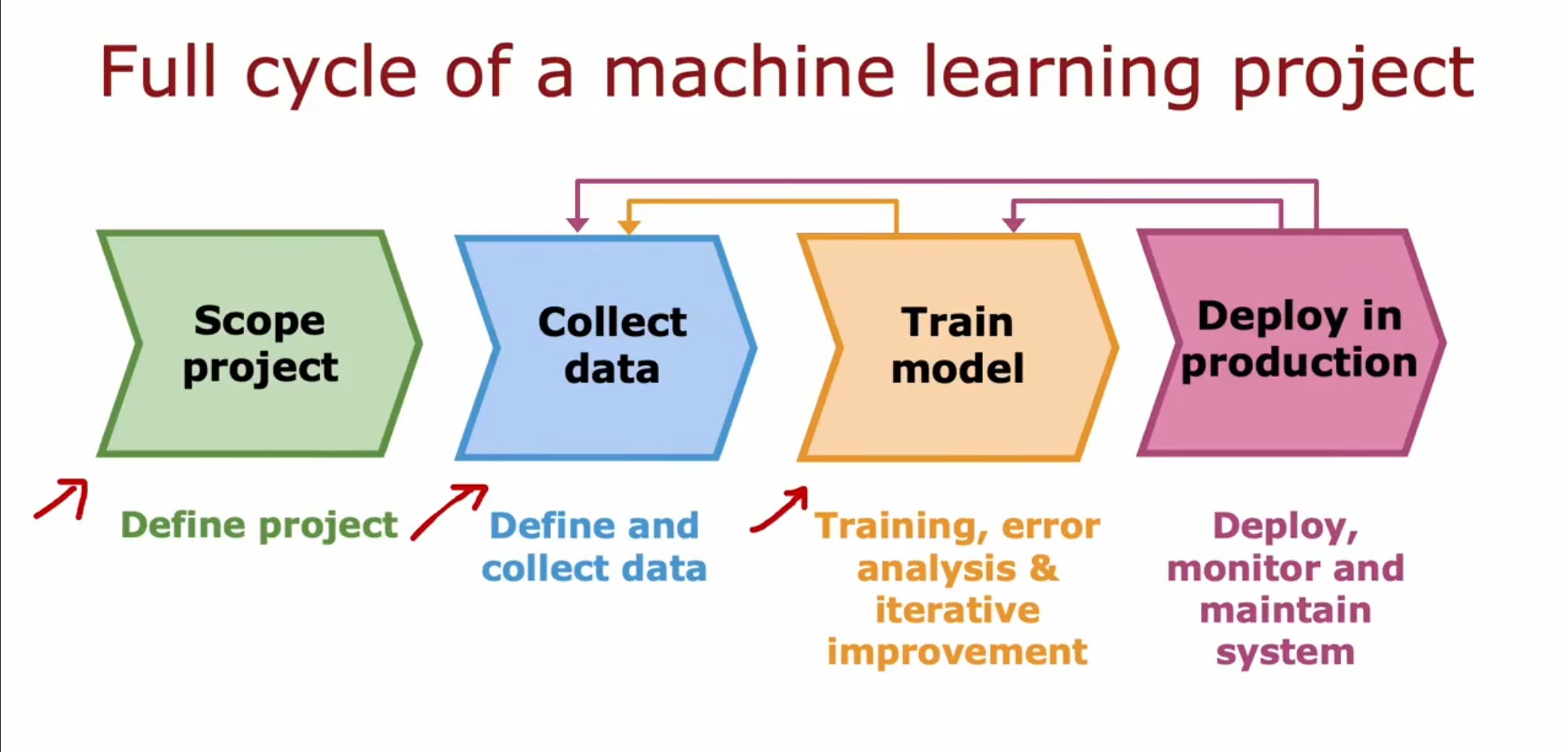
第一步,我们需要确定我们的项目本身和我们应该做些什么。
第二步,我们应该收集数据和贴上相应的标签。
第三步,我们应该对模型进行训练,同时根据训练的结果选择是否要收集更多的数据。
第四步,我们将项目部署在服务器上,通过使用其中的数据可以优化系统性能,同时当我们的模型无法很好的工作的时候可以选择重新训练一个新的模型来替代原有的模型。
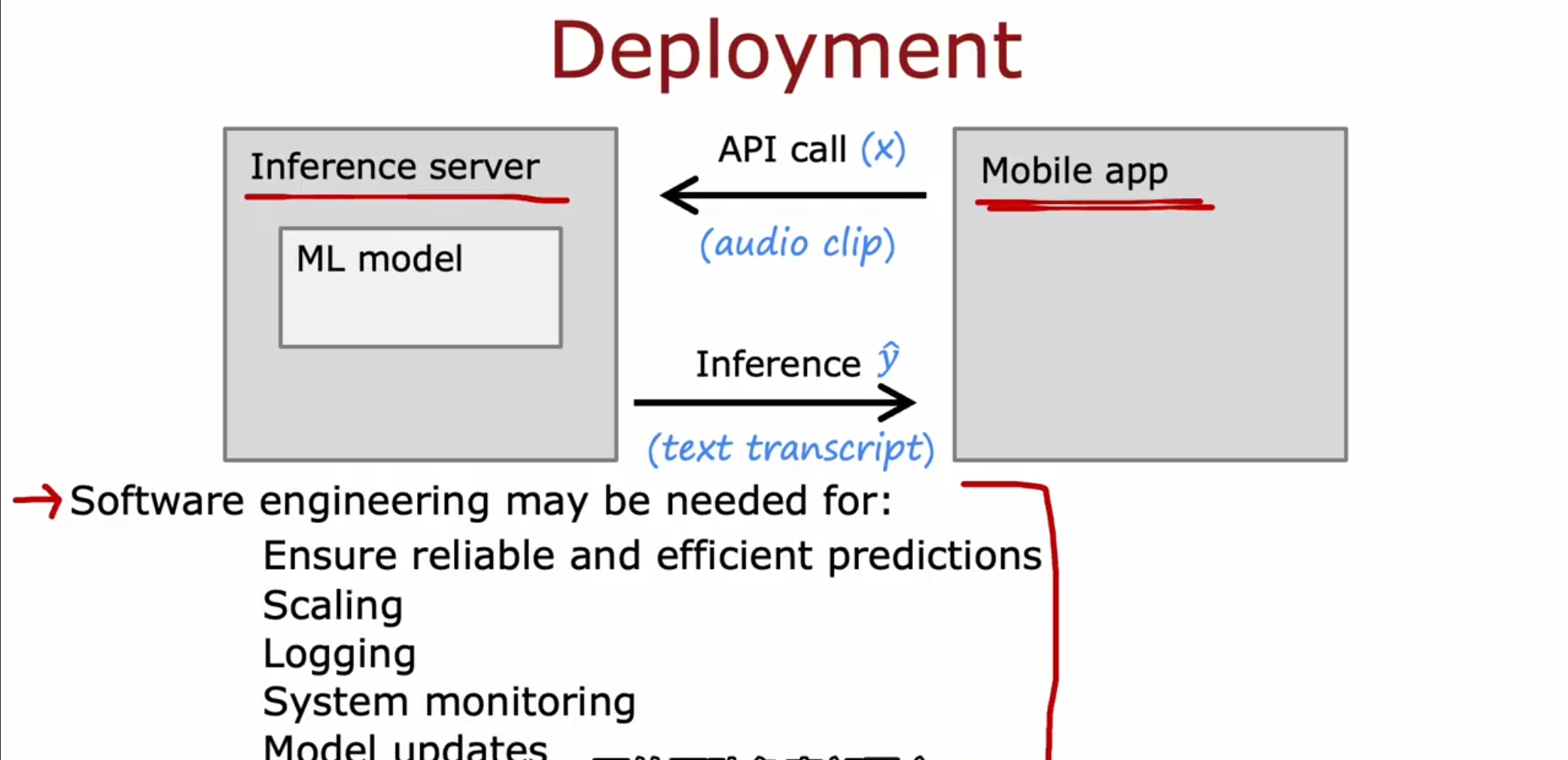
我们在进行项目的部署的时候,可以将其部署在服务器上,我们的应用程序软件可以通过调用提供的API接口使用这个模型所提供的服务。
倾斜数据集的误差指标

对于上述这个很倾斜的数据集,由于呈现阳性的概率只有$ 0.5% $,因此一个只会打印$ print(‘’y=0’’) $的愚蠢算法,实际上的准确率也会比我们的仅有$ 1% $错误率的算法要高,因此仅仅依靠准确率来对于这种数据集进行评估是不公平的,我们需要引入精准率和召回率。

首先绘制一个$ 2\times 2 $的矩阵,我们称之为混淆矩阵。根据这个矩阵,我们可以计算出两个值。
精准率:$ \frac{TP}{TP+FP} $,这代表在你预测为真的事件中,有多少预测正确。
召回率:$ \frac {TP}{TP+FN} $,这代表在所有真事件中,你预测正确的占多少。
高精准率代表预测为阳性的患者很大概率是真的,高召回率代表为一个称阳性的患者可以被检测到。
如此,对于之前仅预测为假的算法,它的精准率和召回率都是为$ 0 $。
精准率和召回率

对于逻辑回归问题来讲,当我们提高阈值,那么我们的精准度就会上升,但是召回率就会下降,相反,如果降低阈值,那么我们的精准度就会下降,但是召回率就会上升,因此我们需要通过手动的方式选择一个合适的阈值。

为了更好的权衡精准率和召回率,我们选择使用一个$ F1 $分数,而不是简单的平均数。
使用$ F1\mathrm{~score}=\frac{1}{\frac{1}{2}{(\frac1P+\frac1R)}}=2\frac{PR}{P+R} $,这样得到的结果更加偏向比较小的值,这也被称为调和平均数。