决策树

引入

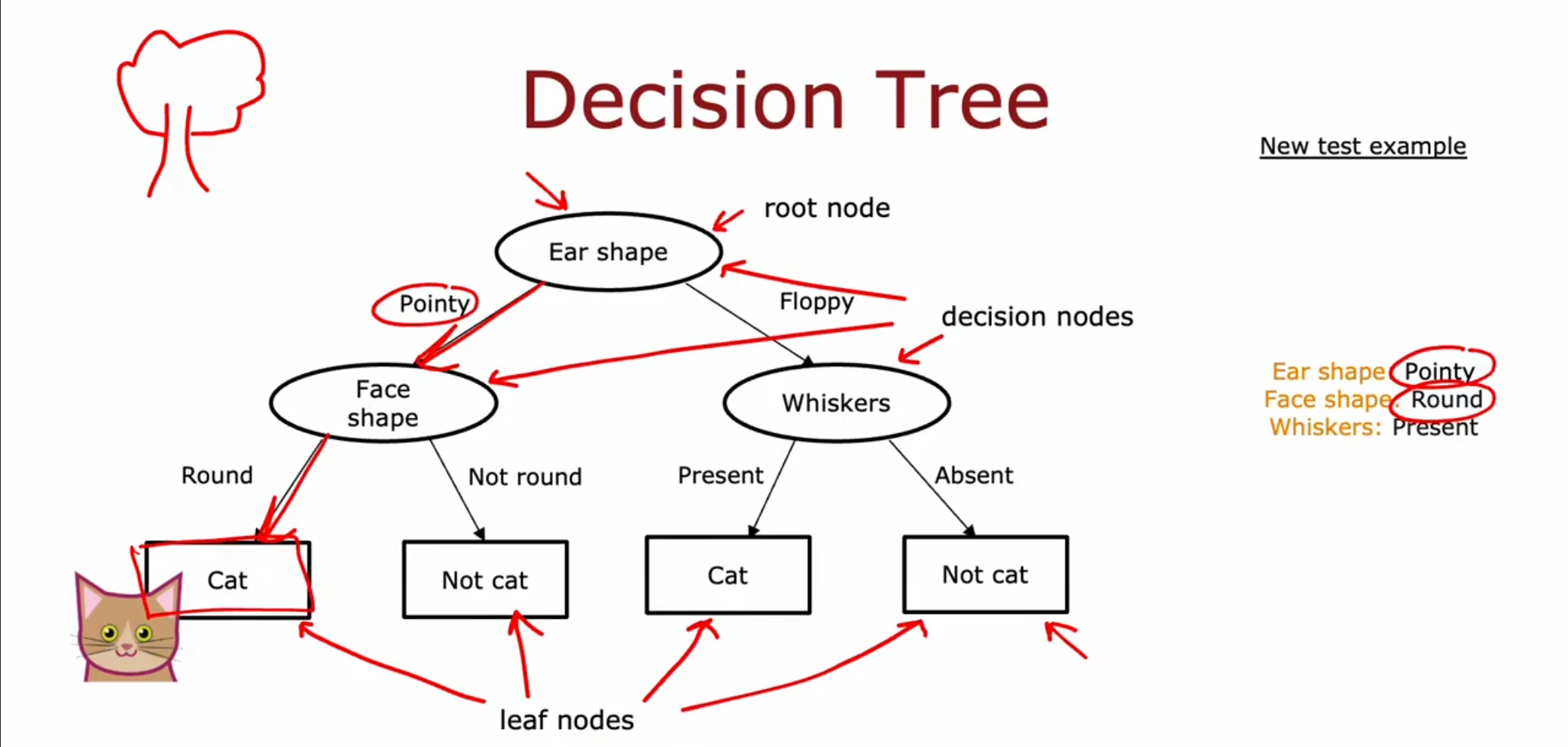
我们引入一个新的模型-决策树，通过这个二叉树我们可以实现对于猫的分类，从根节点出发，判断每个节点是还是否，最终我们在叶子节点得到结果。

学习过程

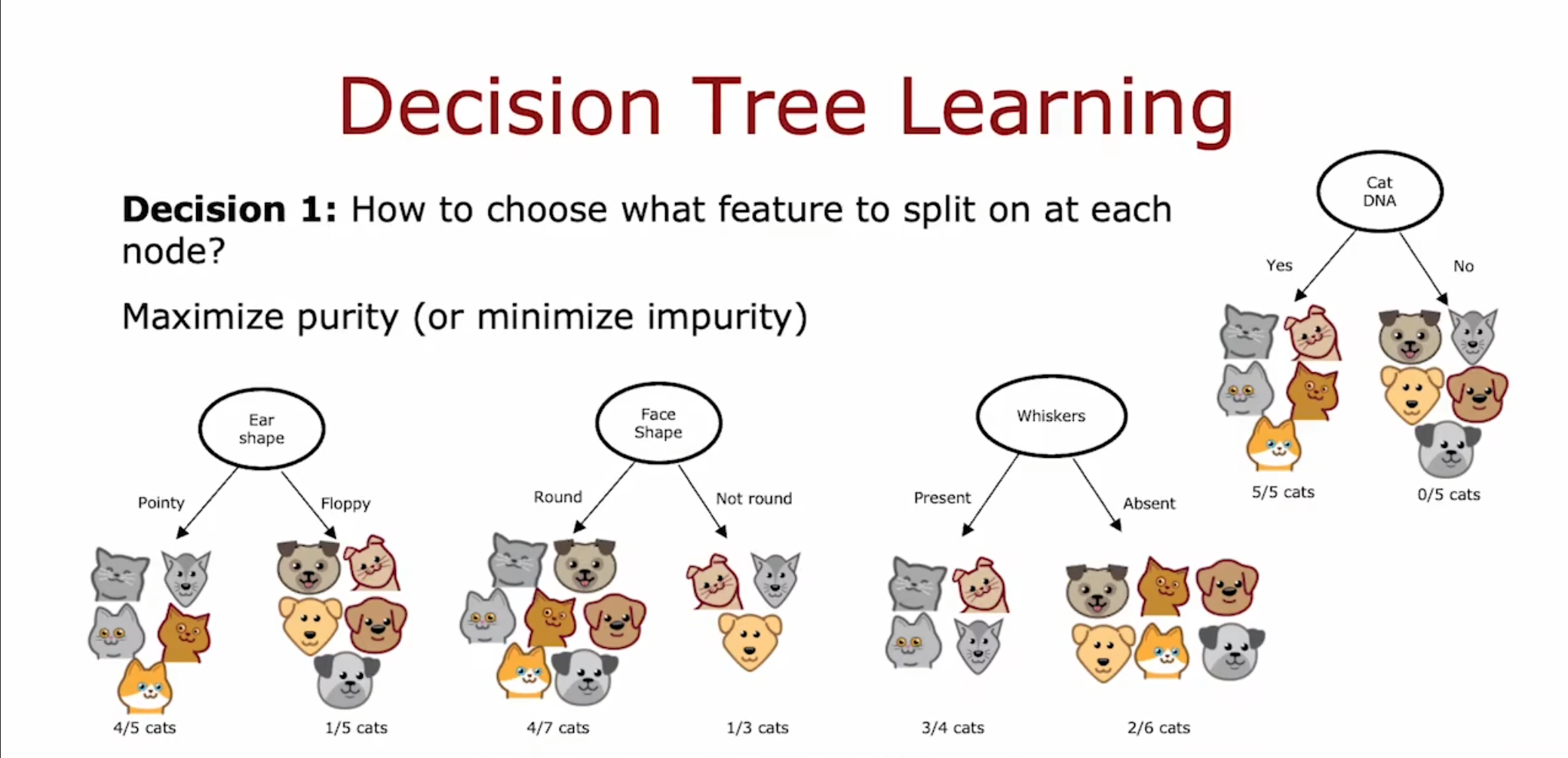
第一步：决定每个节点应该使用什么特征，尽量使得分离后的纯度更大或者杂质更少。

第二步：决定什么时候停止。可以分为以下四种情况：

• 当一个节点的纯度达到$ 100% $
• 当一个节点的深度超过我们限制的最大深度
• 当继续分裂的提高值小于一个阈值时
• 当这个节点的纯度达到一个阈值时

信息熵

为了说明纯度，我们引入了熵这个概念。当有一半为猫，一半为狗的时候显然这个的熵是最高的，也代表是最不纯的。当全部为猫，或者全部为狗的时候则代表熵是最低的，也代表是最纯的。

我们可以使用这个熵函数$H(p_{1})=-p_{1}log_{2}(p_{1})-p_{0}log_{2}(p_{0})$$=-p_1log_2(p_1)-(1-p_1)log_2(1-p_1)$,这个就是信息熵的定义，即一个系统中所有事件的信息量累积和。一个越确定的系统，那么它的信息熵自然也就越小，因此我们可以使用信息熵作为衡量纯度的标准。

关于信息熵，交叉熵的详细解释可以参照这个视频：

“交叉熵”如何做损失函数？打包理解“信息量”、“比特”、“熵”、“KL散度”、“交叉熵”_哔哩哔哩_bilibili

信息增益

信息增益（information gain） 代表的是在一个条件下，信息复杂度（不确定性）减少的程度，也即纯度提高的程度。

我们通过计算每个分裂特征的信息增益，作为一种衡量的标准。

通过$=\mathrm{H(p_1^{root})} -\left(w^{\mathrm{left}}H\left(p_1^{\mathrm{left}}\right)+w^{\mathrm{right}}H\left(p_1^{\mathrm{right}}\right)\right)$这个公式我们可以得到每个分裂特征的信息增益。

完整流程

第一步：将所有的样本放在根节点

第二步：计算所有分裂特征的信息增益，选择其中一个最高的

第三步：通过分裂特征切割数据集，创建左右节点

第四步：直到一定条件停止分裂

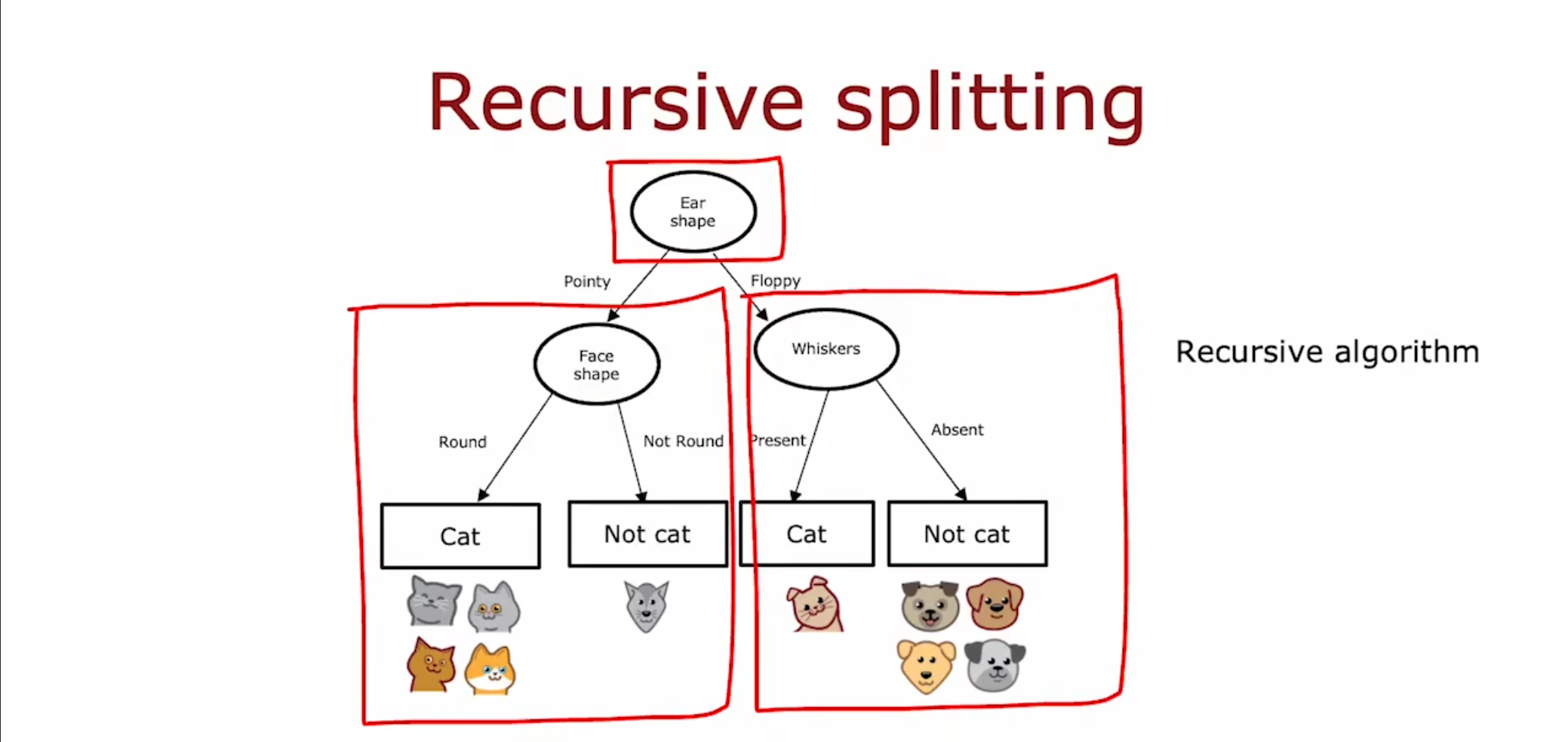
首先在根节点选择的数据集是全部的样本，接着在左节点我们选择被分割的那五个作为样本数据集，在右节点选择另外五个作为数据集，其中每次选择的数据集不同。

根据一定的策略 , 确定哪个属性作为树根 , 然后每个子树 , 在确定剩余的哪个属性作为子树的树根 , 这是递归问题 ，就像二叉树的深度优先遍历一样。

独热码

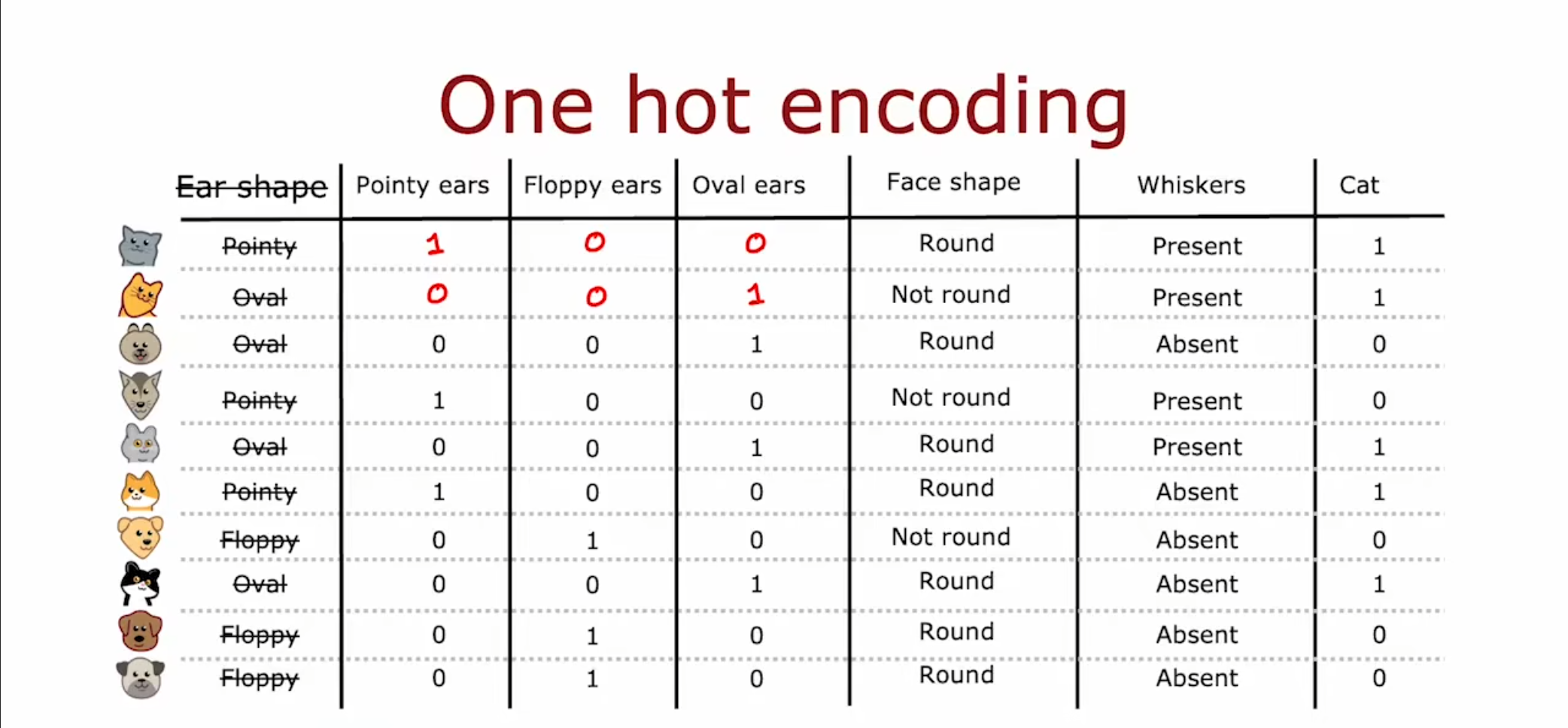
为了处理两个以上的离散特征值，我们选择了使用独热码的形式，将其中符合特征的值设置为$ 1 $，使用这种方式就可以表示$ k $个的离散特征值，接下来处理连续的特征值。

连续特征值

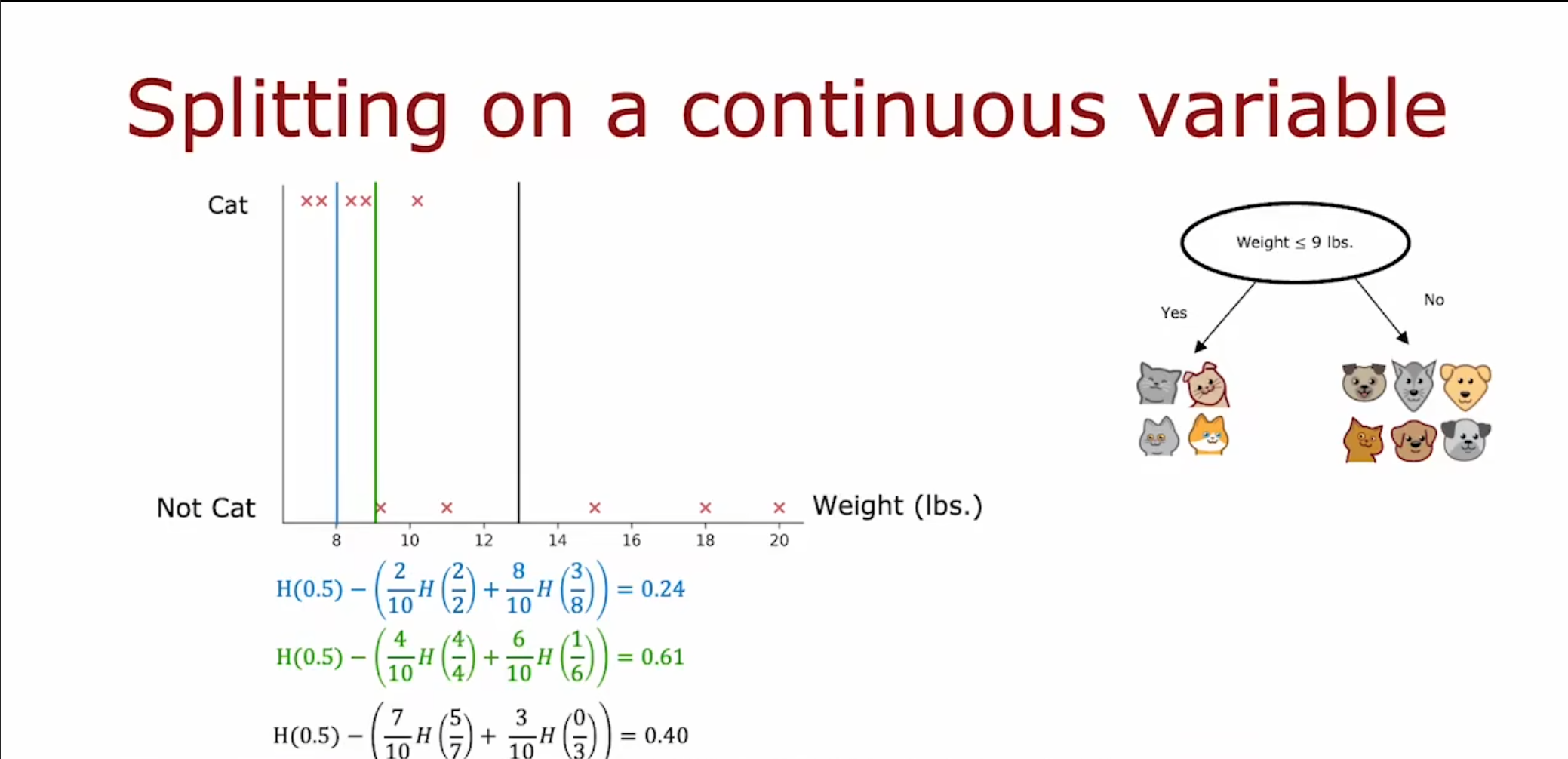
对于连续的特征值，我们可以尝试不同的阈值，分别计算对应的信息增益，最终计算出最高的那个阈值，并使用这个作为我们的分裂特征。

回归树

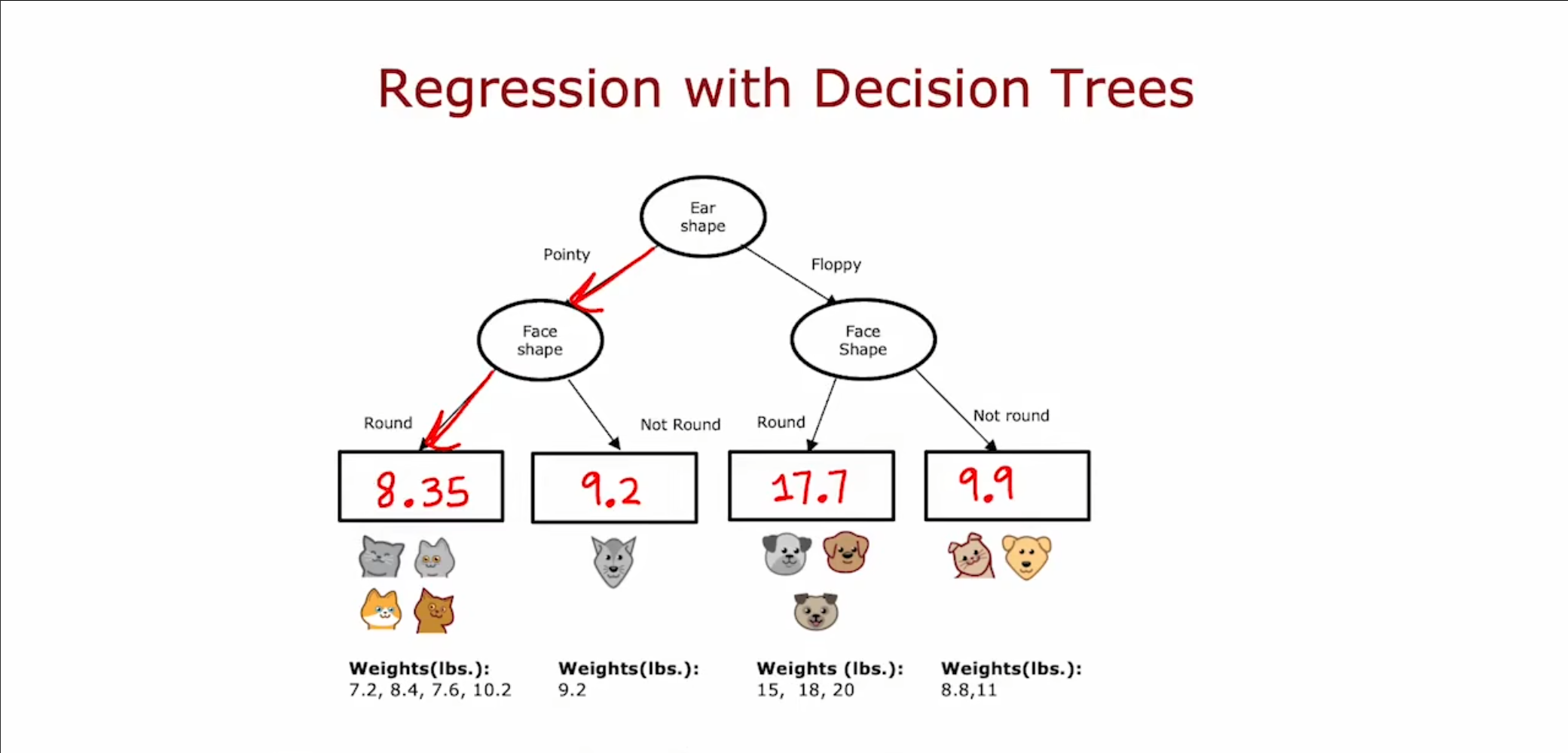
我们对之前的决策树进行泛化操作，使得原本仅可以判断分类的决策树也可以实现回归问题，跟决策树相同，仅仅在输出结果时将原本的分类改为分类的重量平均值，实现了对于重量的预测。

在计算应该选择那个节点作为新节点时，我们不再选择使用信息熵作为需要的指标，而是使用方差，最终我们计算出减少方差最多的那个节点，将其选择为分裂节点。

多决策树

一棵树对于数据是很敏感的，我们仅仅改变其中的一个样本，我们选择的信息增益最高的分裂特征可能就会发生改变从而得到不同的左右节点，因此我们需要使用多颗决策树同时决策。

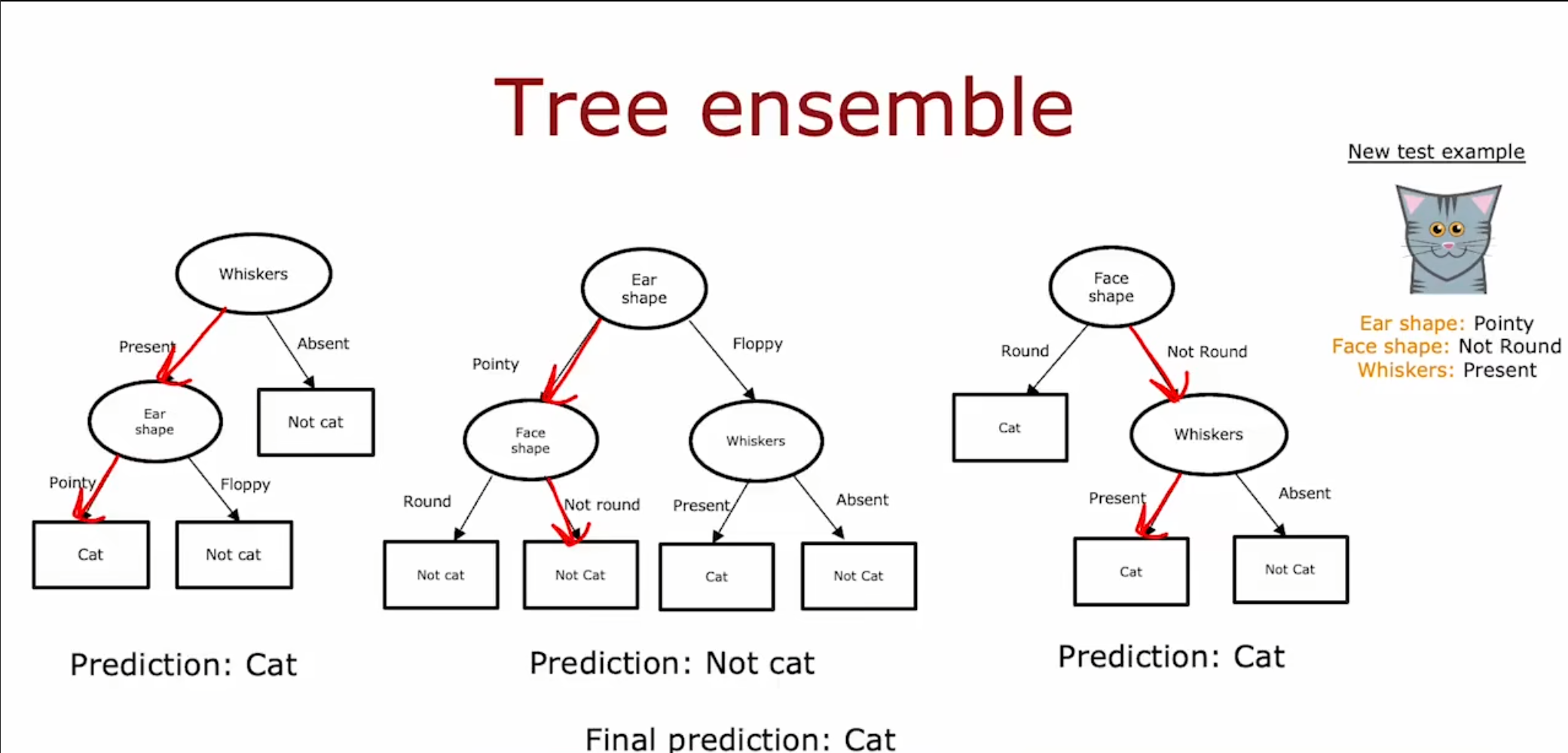
我们使用三颗决策树对于同一个样本进行预测，最终通过最多数的投票做出正确预测。

有放回抽样

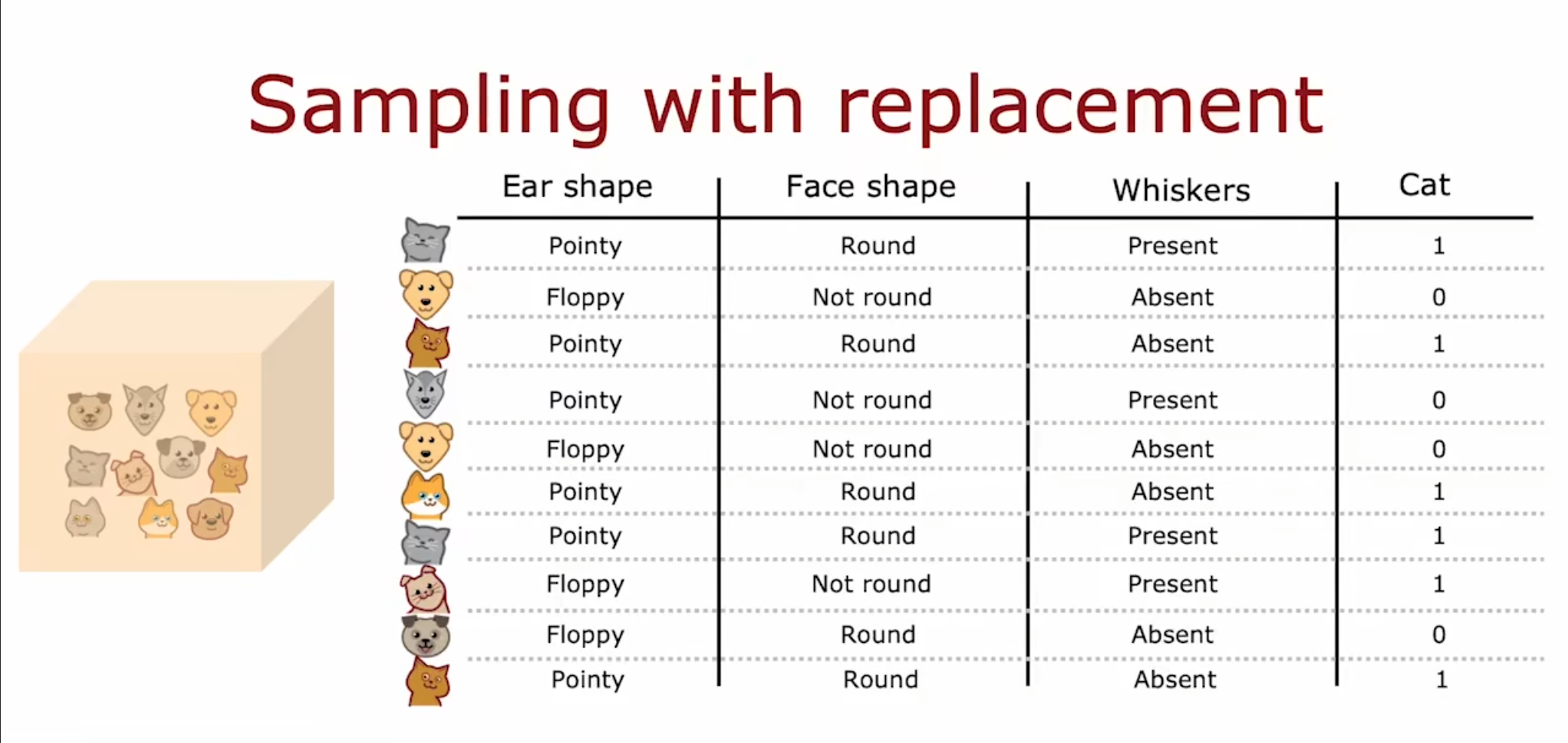
我们将要抽样的数据集放在一个袋子里，每次选择其中一个，然后放回继续抽取，最终我们可以得到一个跟原先数据集很相似，但是又不完全相同的新的数据集，这是构造决策树集合的关键步骤。

随机森林

我们循环$ B $次，每次都按照之前有放回抽样的方式这样就可以构建$ B $个决策树，但是即使这样我们的根节点还是有很大的概率选择相同的分裂特征，因此我们接下来使用在每个节点随机选取属性的方式构建随即森林。这种方式也称为$ Bagged \enspace decision \enspace tree $。

1. 一个样本容量为N的样本，有放回的抽取N次，每次抽取1个，最终形成了N个样本。这选择好了的N个样本用来训练一个决策树，作为决策树根节点处的样本。
2. 当每个样本有M个属性时，在决策树的每个节点需要分裂时，随机从这M个属性中选取出m个属性，满足条件m << M。然后从这m个属性中采用某种策略（比如说信息增益）来选择1个属性作为该节点的分裂属性。
3. 决策树形成过程中每个节点都要按照步骤2来分裂（很容易理解，如果下一次该节点选出来的那一个属性是刚刚其父节点分裂时用过的属性，则该节点已经达到了叶子节点，无须继续分裂了）。一直到不能够再分裂为止。注意整个决策树形成过程中没有进行剪枝。
4. 按照步骤1~3建立大量的决策树，这样就构成了随机森林了。

XGBoost

目前来说，同质个体学习器的应用是最广泛的，一般我们常说的集成学习的方法都是指的同质个体学习器。而同质个体学习器使用最多的模型是CART决策树和神经网络。同质个体学习器按照个体学习器之间是否存在依赖关系可以分为两类，第一个是个体学习器之间存在强依赖关系，一系列个体学习器基本都需要串行生成，代表算法是boosting系列算法，第二个是个体学习器之间不存在强依赖关系，一系列个体学习器可以并行生成，代表算法是bagging和随机森林（Random Forest）系列算法。

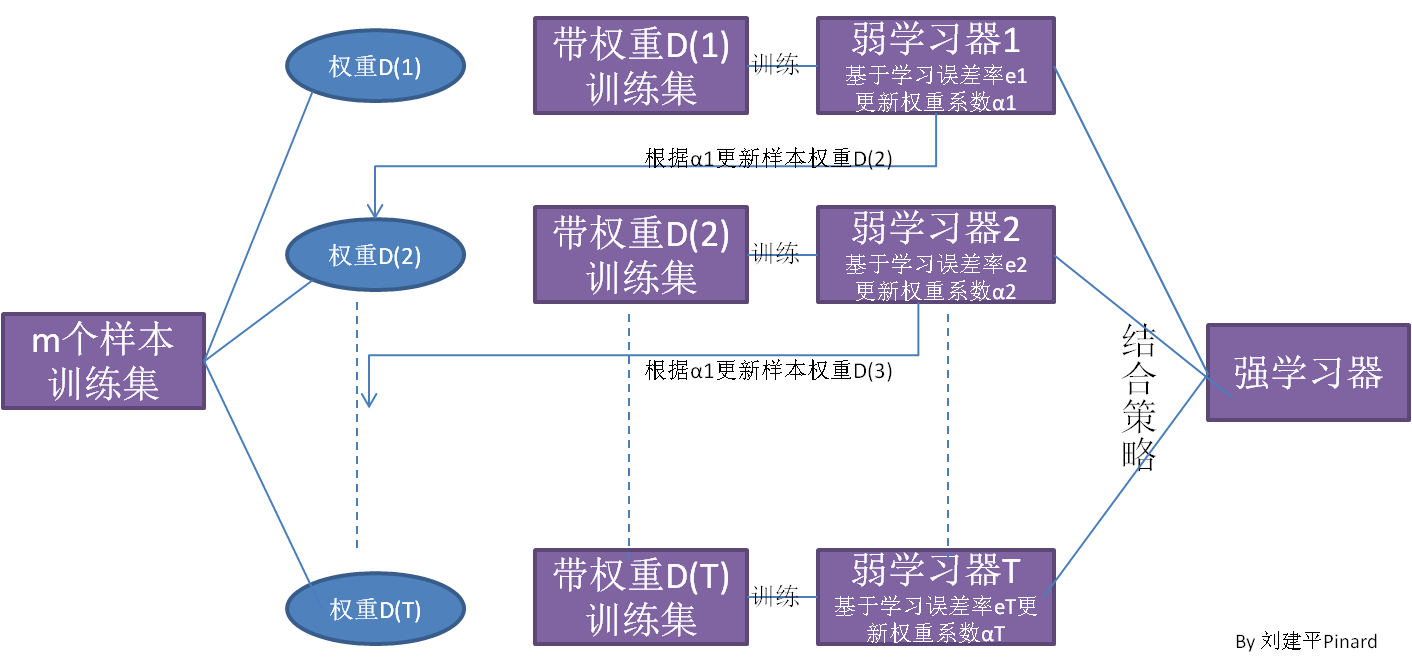
其中$ XGBoost $就是$ boosting $系列中的一个重要算法，它通过不断的调整学习器的权重，仅使用原始的训练集，而不是生成多个训练集，同时还内置了正则化以防止过度拟合，被广泛的用于各大比赛中。

参照：

集成学习原理小结 - 刘建平Pinard - 博客园

决策树VS神经网络

决策树：

• 适合结构化数据，不推荐处理非结构化的图形和声音数据
• 训练速度快
• 小型决策树可以被人为解释其中每一步的作用

神经网络：

• 对于结构化和非结构化数据都工作的很好
• 训练速度比决策树慢
• 当训练数据量不足时，可以使用迁移学习
• 当一个系统需要多个模型同时工作时，更容易构建大型的神经网络，决策树一次只能训练一颗