多元线性回归
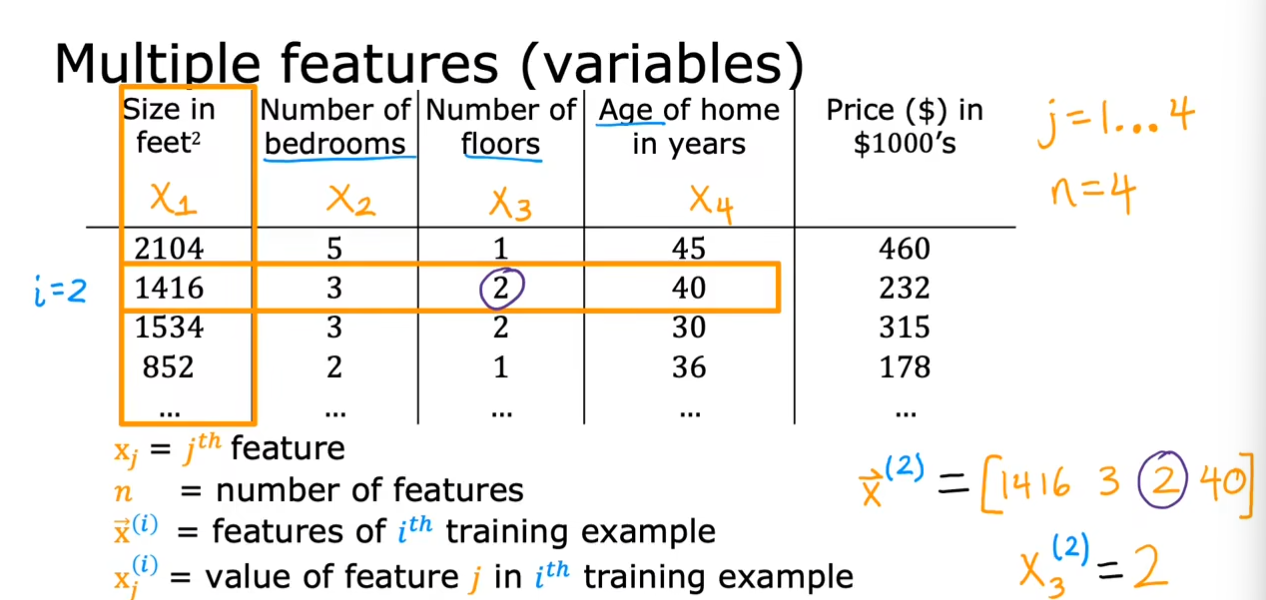
在前面的章节中,我们仅仅使用了一个变量$ x $,接下来我们将考虑多个变量的影响。
$ x_j $:第$ j $个特征
$ n $:表示特征的数目,有$ n $列
$ \vec{\mathrm{x}}^{(i)} $:表示第$ i $个训练示例,也可以称为一组行向量
$ x_{j}^{(i)} $:表示第$ j $个特征的第$ i $个训练示例
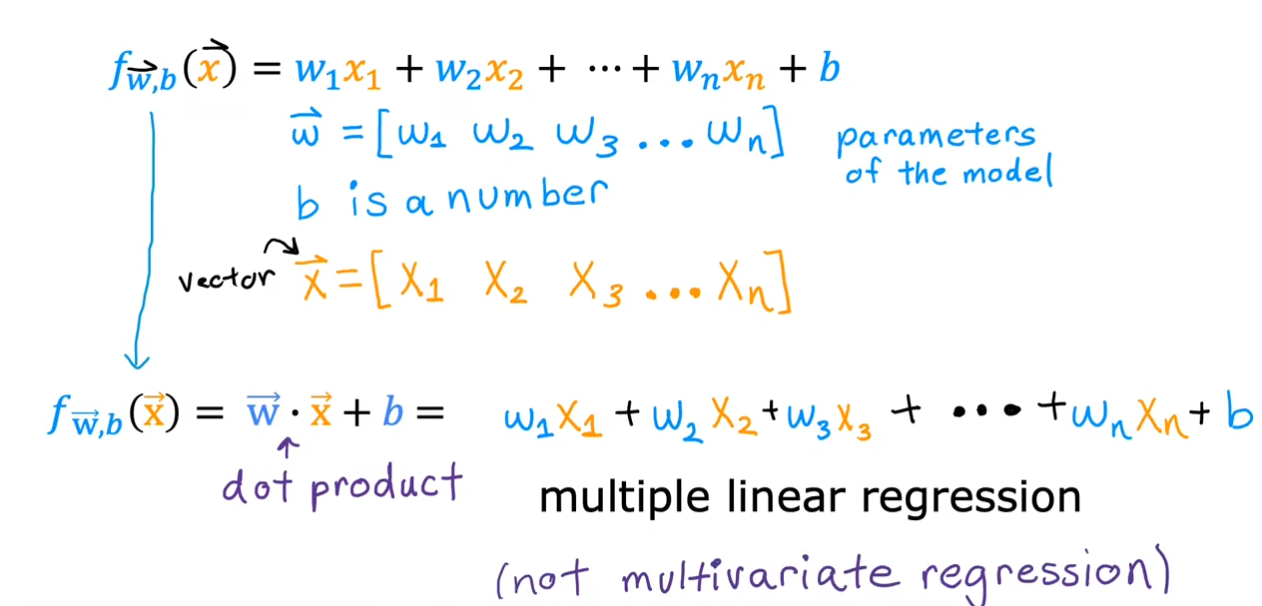
我们可以将上面的逐个相乘再相加的式子写成一个向量之间点乘的形式,更加简洁。通过引入多个特征,这也被称为多元线性回归。
向量化

对于$ f_{w,b}(x) $的表示我们有三种不同的方式,分别为直接相加,循环,使用向量表示。前两者不仅在编写上不如第三种,而且由于考虑到numpy可以实现GPU加速,在运算速度上也是胜过前两者。
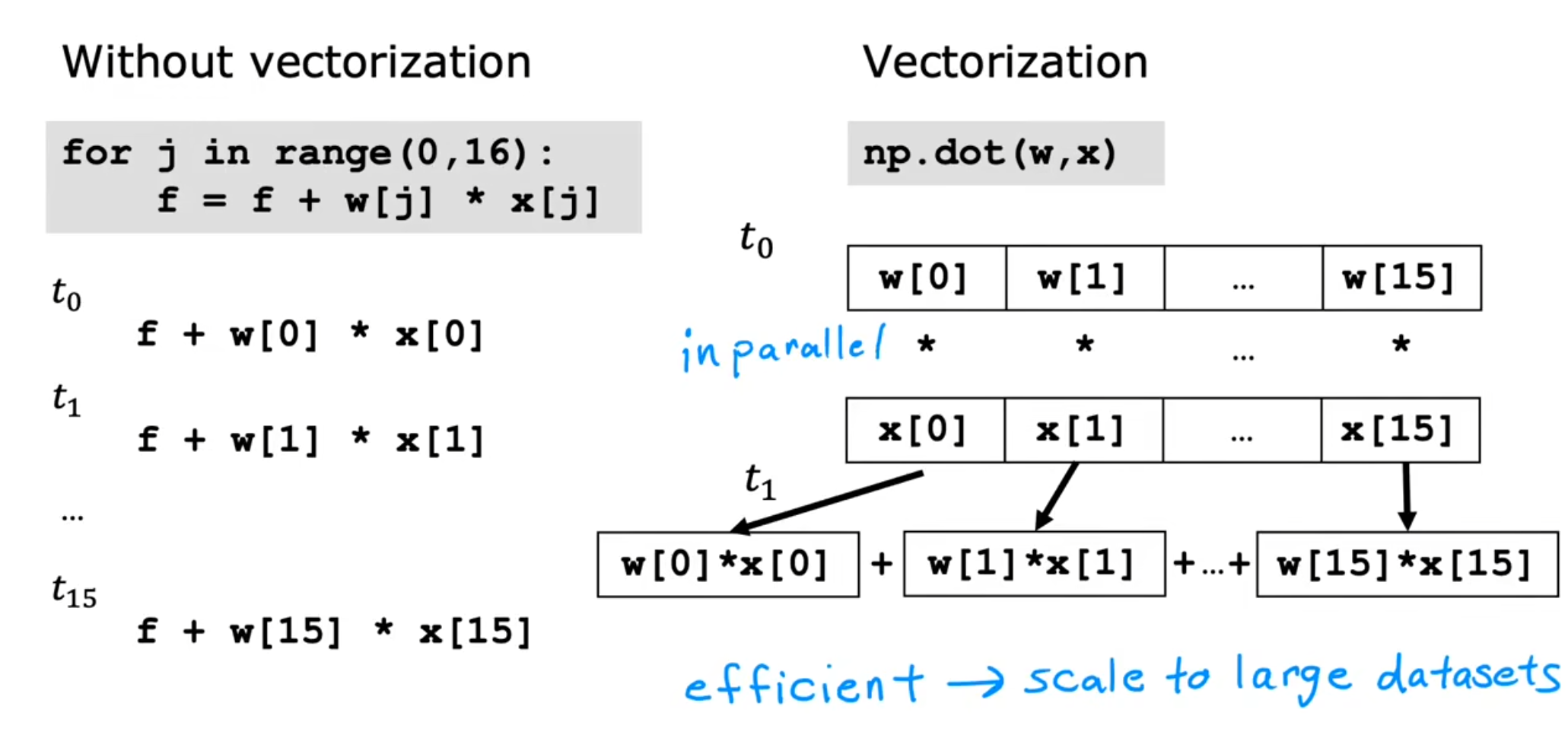
可以看到由于numpy可以将$ w,x $之间并行处理,不需要一步步的计算,因此速度远远快于累加的循环方法。
梯度下降

我们将$ w $向量化,可以得到右边的式子。
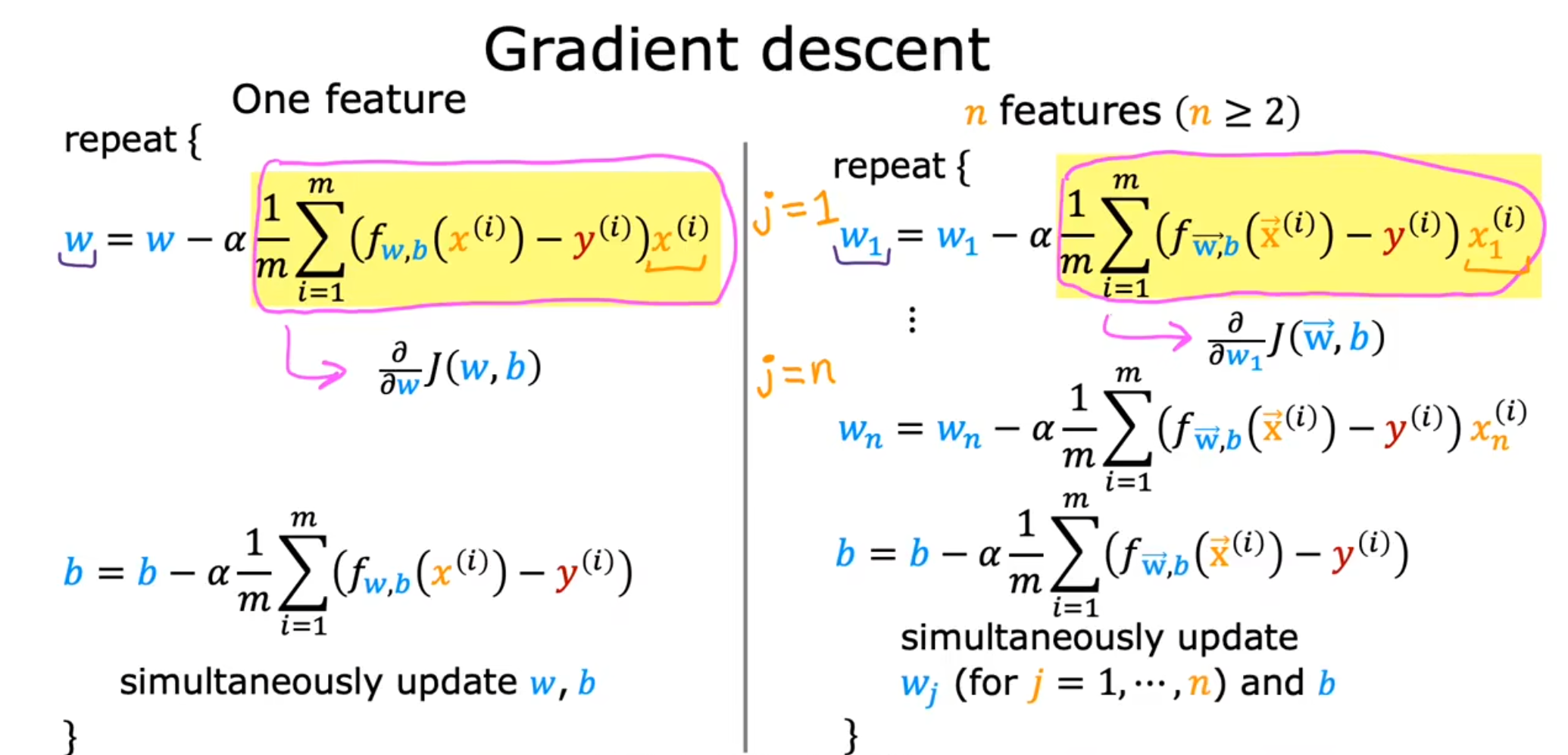
需要注意$ w_j $的计算,最后的$ x_{j}^{(i)} $是一个数,而不是一个向量。
特征缩放

像上面这个例子一样,由于面积这个特征的取值范围远远大于房间数目这个取值范围,因此我们可能会需要一个更聪明的模型才可以选择一个合适的$ w1,w2 $使得预估结果更加合理。
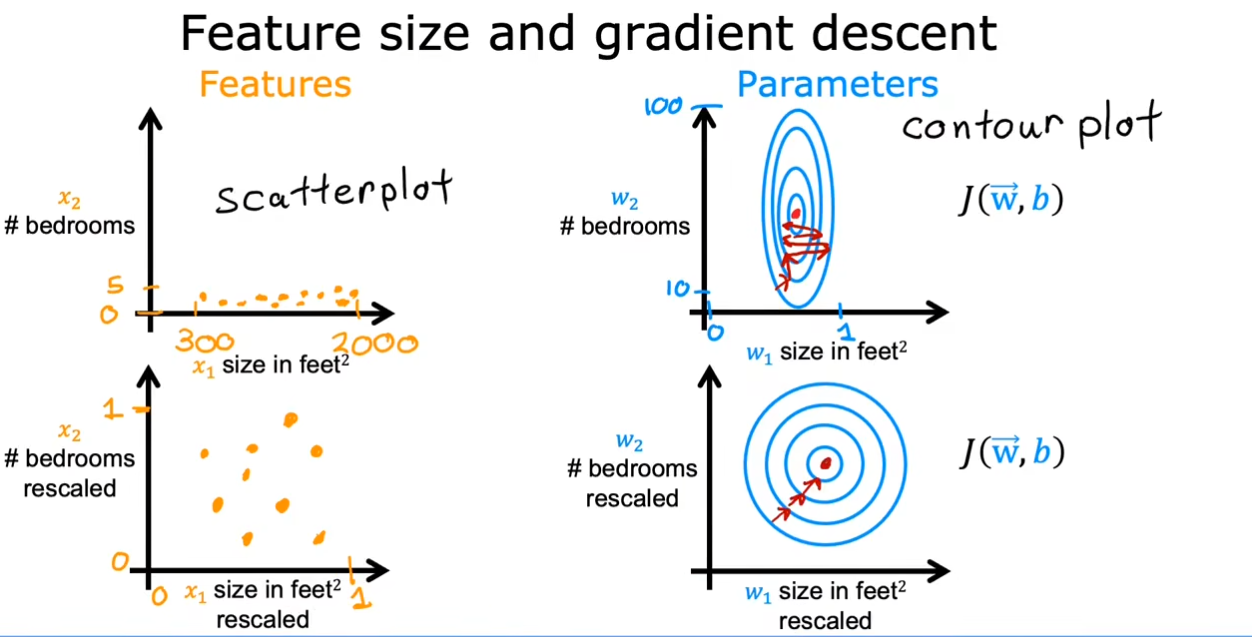
即使我们的模型足够聪明,选择了合适的$ w1,w2 $。但是我们可以看到上边两幅图中的特征值和等高线的分布都是十分不均匀的,这可能会导致我们在进行梯度下降的时候会折返多次。这时候就需要我们对于特征值进行一些缩放,使其可以更加均匀的分布,在进行梯度下降时可以更快的得到最小值。
- 直接缩放
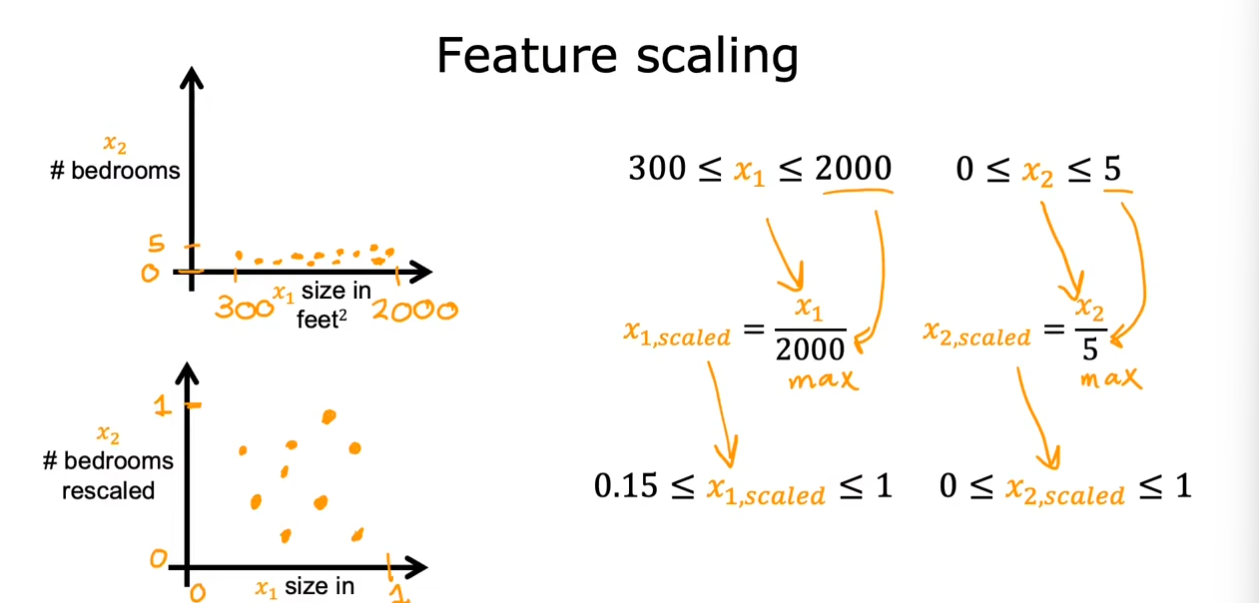
采用直接除以最大值的方式,使其范围在$ [0,1] $之间。
- Mean normalization

使用$ x_{new}=\frac{x-mean(x)}{max(x)-min(x)} $,通过减去均值在除以范围,使得范围在$ [-1,1] $之间。
- Z-score normalization
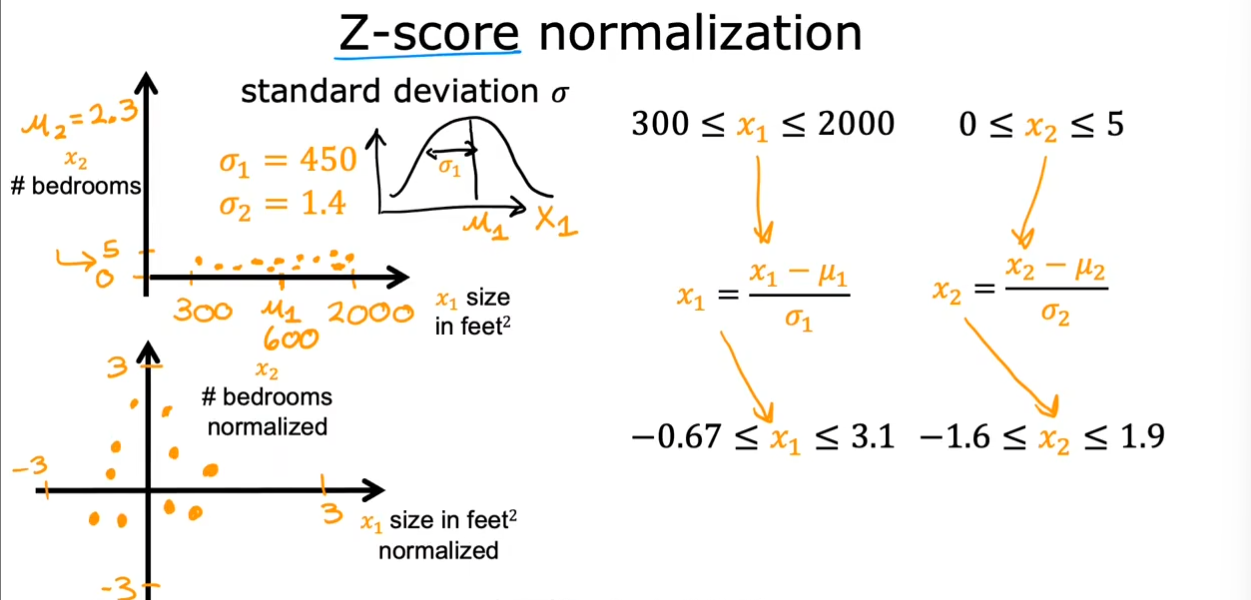
使用$ x_{new}=\frac{x-\mu}{\sigma} $,将数据变换为均值为$ 0 $,标准差为$ 1 $的分布切记,并非一定是正态的,只有原来就是正态分布才会变成标准正态化。
同时由于这些变化都是线性的,对于数据本身的顺序不会造成影响。
梯度下降收敛

通过左边的曲线我们看到当迭代次数达到$ 300 $时,我们的曲线的减少已经接近为0,在$ 400 $时已经接近于平衡。同时我们也可以使用一个$ \epsilon $来进行判断,当减少量小于这个数时,代表该曲线已经收敛。
选择合适的学习率
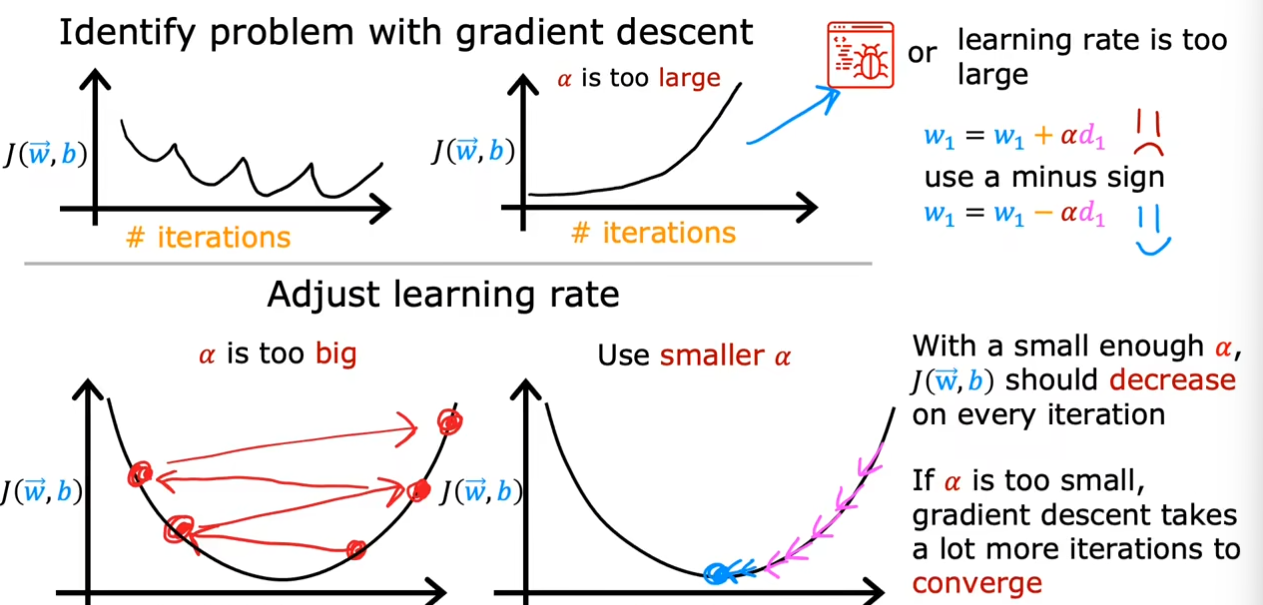
如果曲线不是呈现前面的逐渐下降直到最终趋近于平衡的话,而是不断起伏或者上升,那么就代表程序本身出现了bug或者学习率设置的过大,使得无法找到最小值,这时候我们需要调整这个数,使得曲线可以慢慢下降到最小。
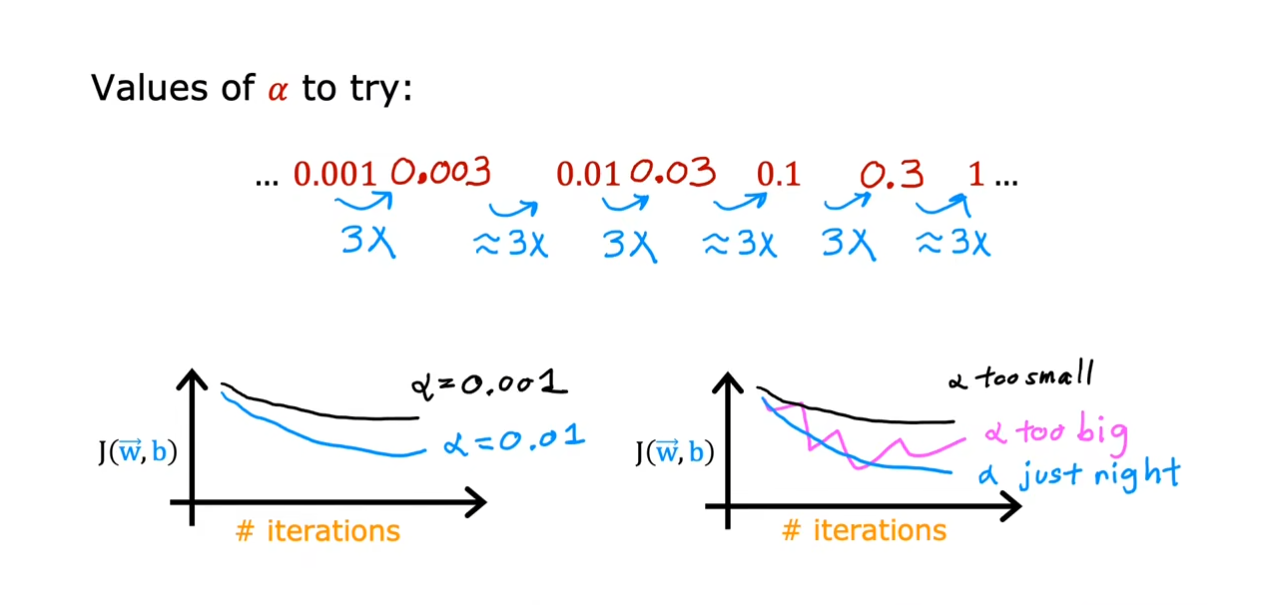
在最开始选择一个很小的学习率,不断地增大直到无法收敛,然后根据这样找到一个合适的值。
特征工程
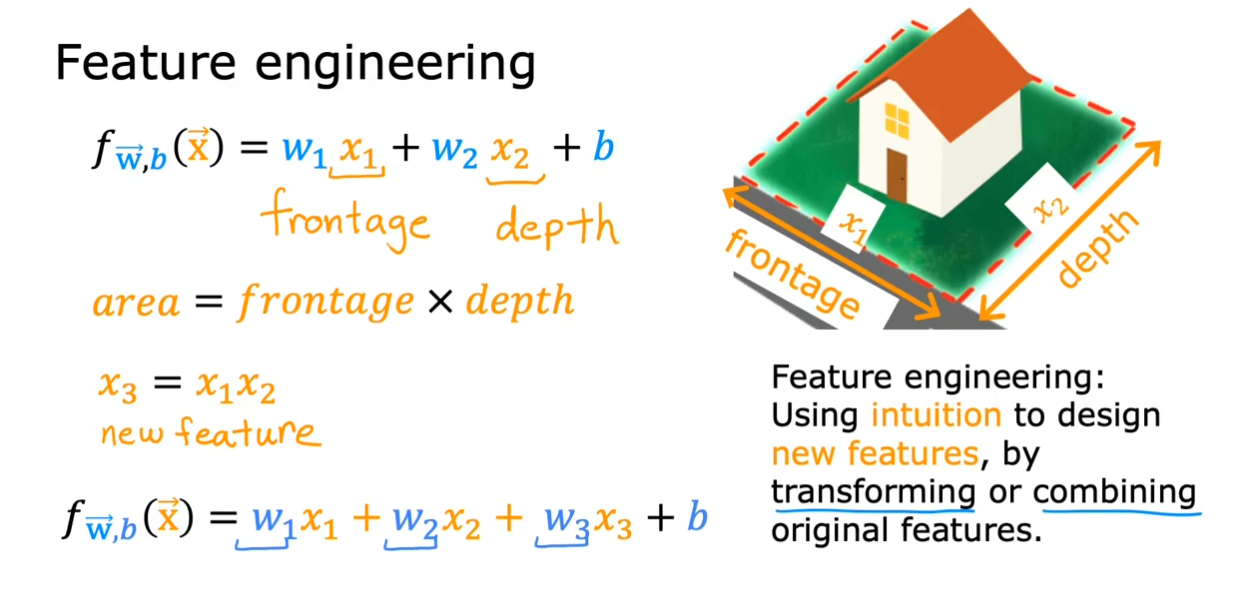
有时候原生特征不能完全满足预测的要求,那么可以根据一个或者多个原生特征衍生出其它可用或不可用的特征,这一过程称为“特征衍生”。特征衍生是特征工程一个比较重要的组成部分,它需要花费比较多的精力和时间尽量去认识原生特征和具体的预测命题,然后根据原生特征的特点构造出一些衍生特征。
例如我们一开始使用长度和宽度分别作为特征进行预估,但是可以使用这两个值的乘积也就是面积作为新的特征进行预测,使得结果更加精准。
多项式回归
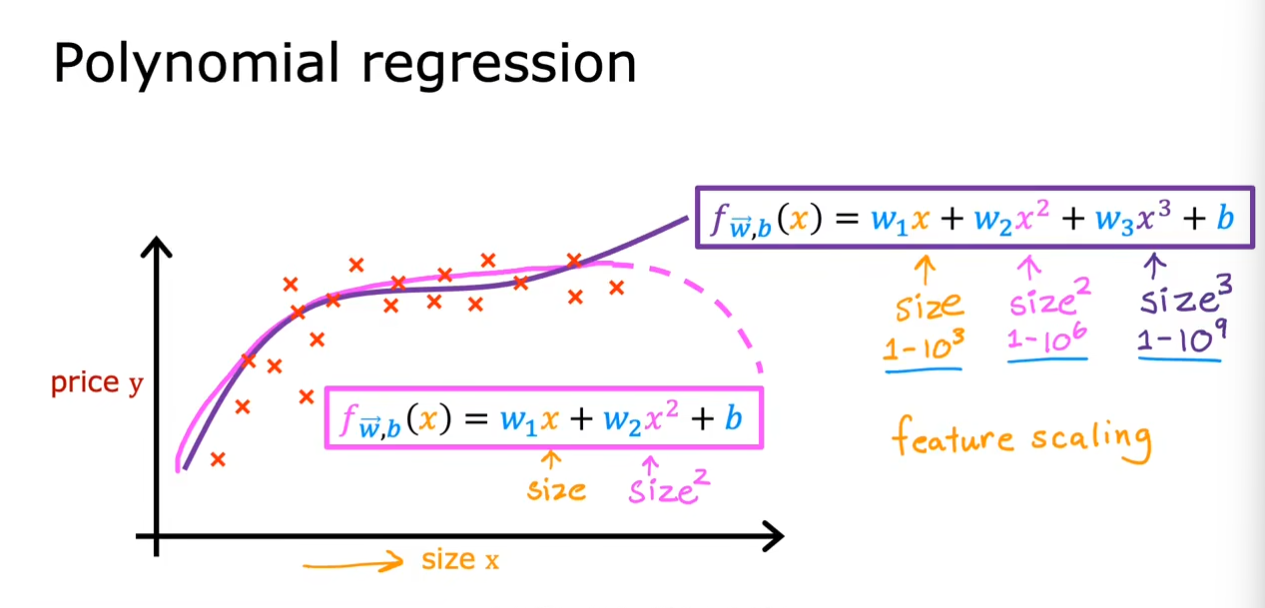
我们已经使用了很久的$ f(w,b)=wx+b $,现在让我们使用一个曲线来更好地拟合这些数据。
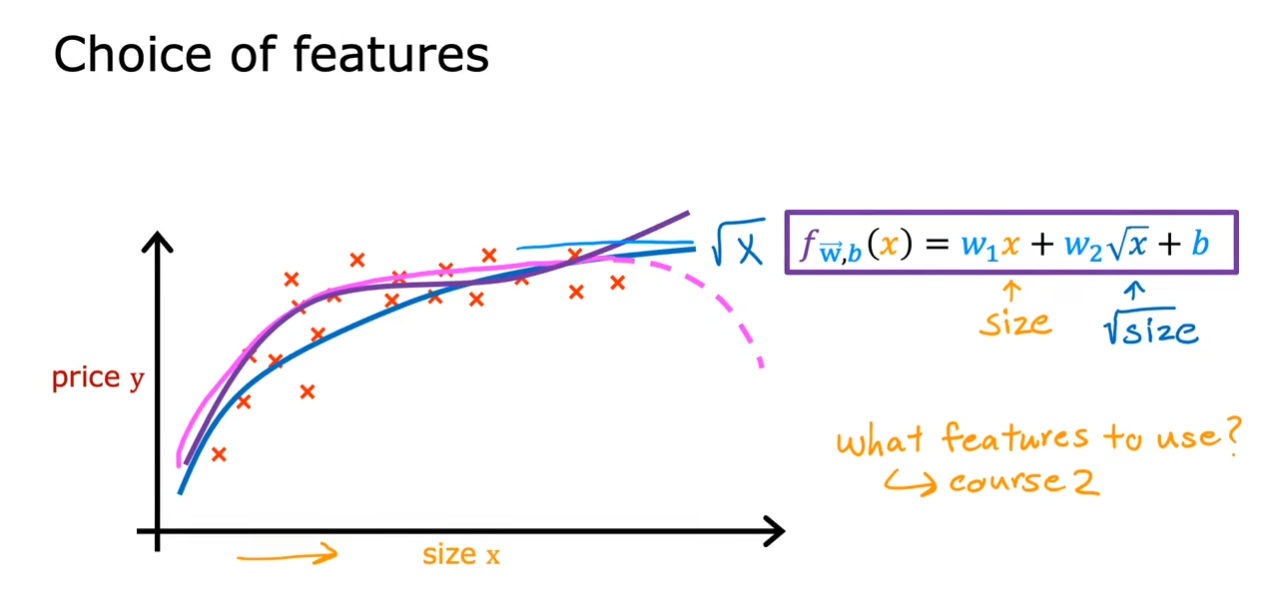
我们可以使用不同的多项式函数,使得我么的曲线更好的拟合数据。
正规方程
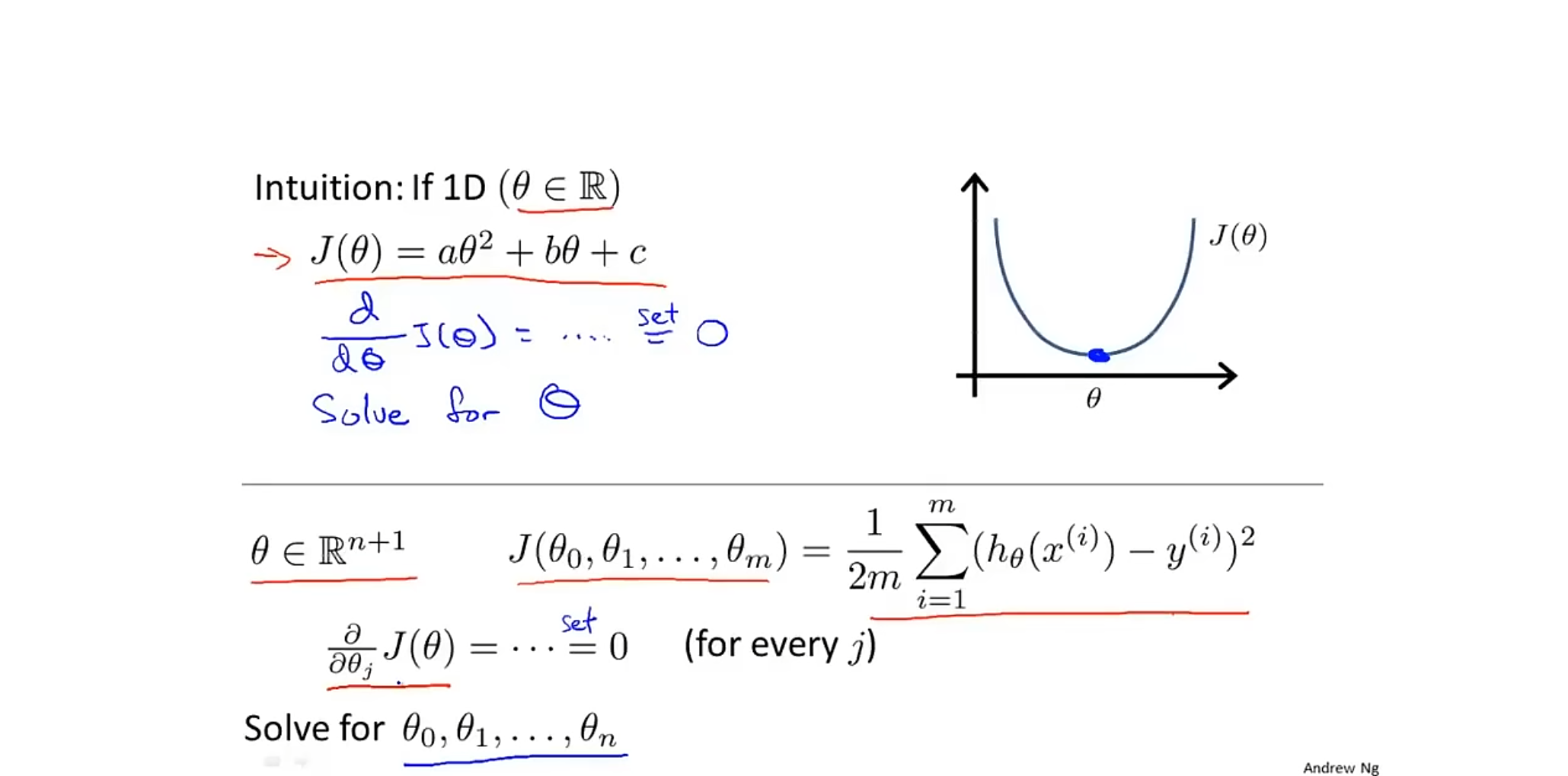
我们可以看到当偏微分为$ 0 $时,我们可以得到这个代价函数的最小值。

根据以上推导我们可以得到一个公式$ \theta=\begin{pmatrix}X^TX\end{pmatrix}^{-1}X^T\vec{y} $,通过这个式子我们无需在进行迭代可以直接得到我们需要的$ \theta $。
对于其它的方式也可以参看刘建平老师的博客
机器学习中的矩阵向量求导(四) 矩阵向量求导链式法则 - 刘建平Pinard - 博客园
假如我们有$ m $个训练样本,$ n $个特征变量。
| 梯度下降法 | 正规方程 |
|---|---|
| 缺点: 1. 需要选择学习速率$ α $。 2. 需要更多次的迭代 3. 特征值范围相差太大时需要进行特征缩放。 |
缺点: 1. 当特征数$ n $很大时,运算的很慢,因为求解逆矩阵的时间复杂度很高,属于$ O(n^3) $。 |
| 优点: 1. 当特征数$ n $很大时,也可以正常工作。 |
优点: 1. 不需要选择学习速率$ α $。 2. 不需要多次迭代 3. 不需要特征缩放 |
| 当$ n<10000 $时,通常使用正规方程,当$ n>=10000 $时,要考虑使用梯度下降。一些更加复杂的算法仅可以使用梯度下降。 |

同时我们需要注意并不是所有的情况$ X^TX $都是可逆的,当$ X $中的特征$ X1,X2 $出现线性相关时,或者需要的特征数$ n $大于等于($ n $等于$ m $时需要满足$ det(X) $不等于$ 0 $)给出的样本数$ m $的个数时会出现不可逆的现象。从数学的角度来看就是矩阵不满秩。
可以采取的措施就是删掉一些多余的特征,或者使用正则化。