线性回归

术语

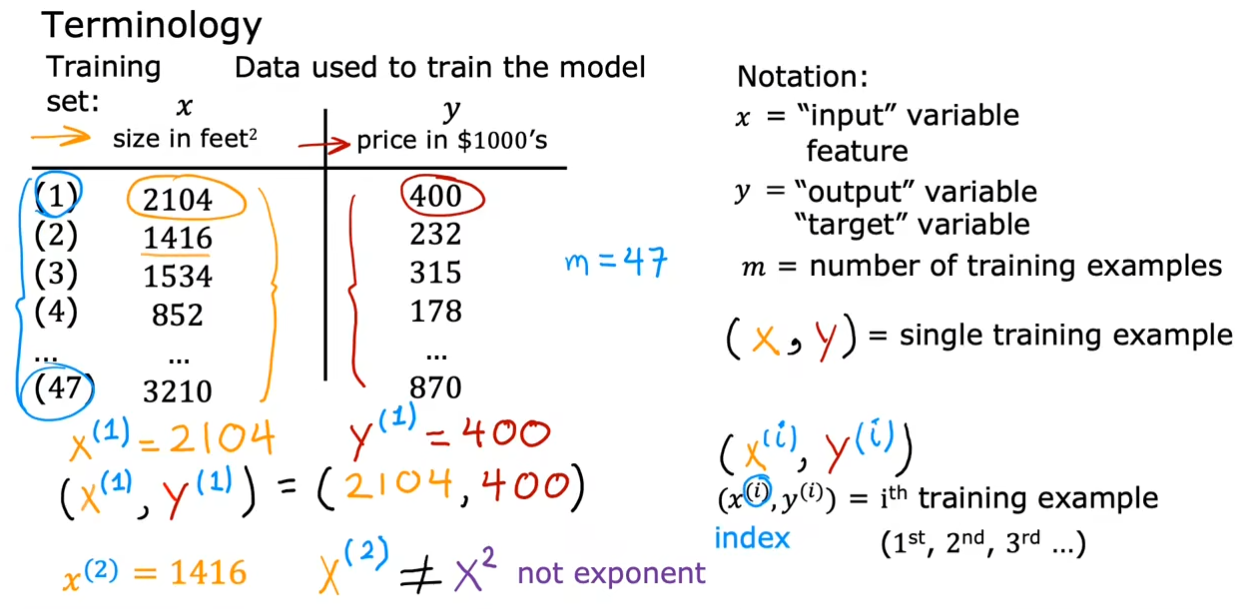
训练集：用于训练模型的数据

$ x $：输入变量，也称为特征或输入特征

$ y $：输出变量，也称为目标变量

$ m $：训练样本的总数

$ (x,y) $：一个训练示例

$ (x^{(i)},y^{(i)}) $ = 第 i 个训练示例

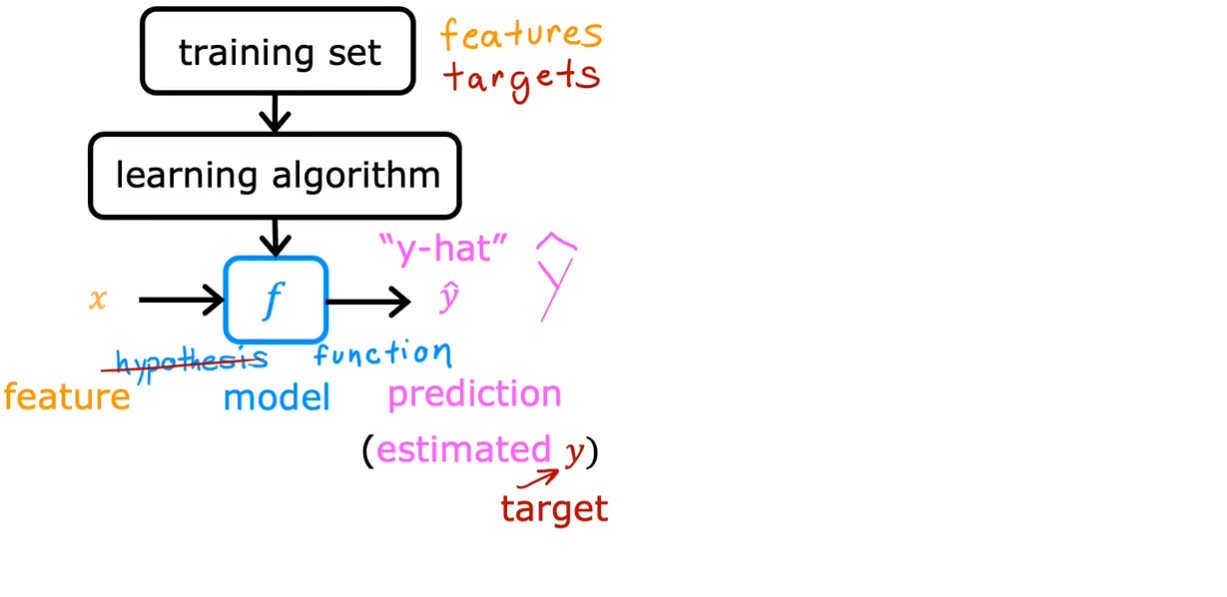
$ f $：模型，获取输入并给出对应的输出

$ x $：输入或输入特征

$ \hat{y} $：预测，也称为估计值

$ f_{w,b}(x) = wx + b $等价于$ f(x)=wx+b $

也被称为单变量线性回归

$ w,b $：参数，也被称为系数或者权重

代价函数

为了找到合适的$ w,b $，我们使用了$ J(w,b)
$作为代价函数来判断，最终使得我们得到的$ \hat{y}^{(i)} $尽量的接近于$ y^{i} $。

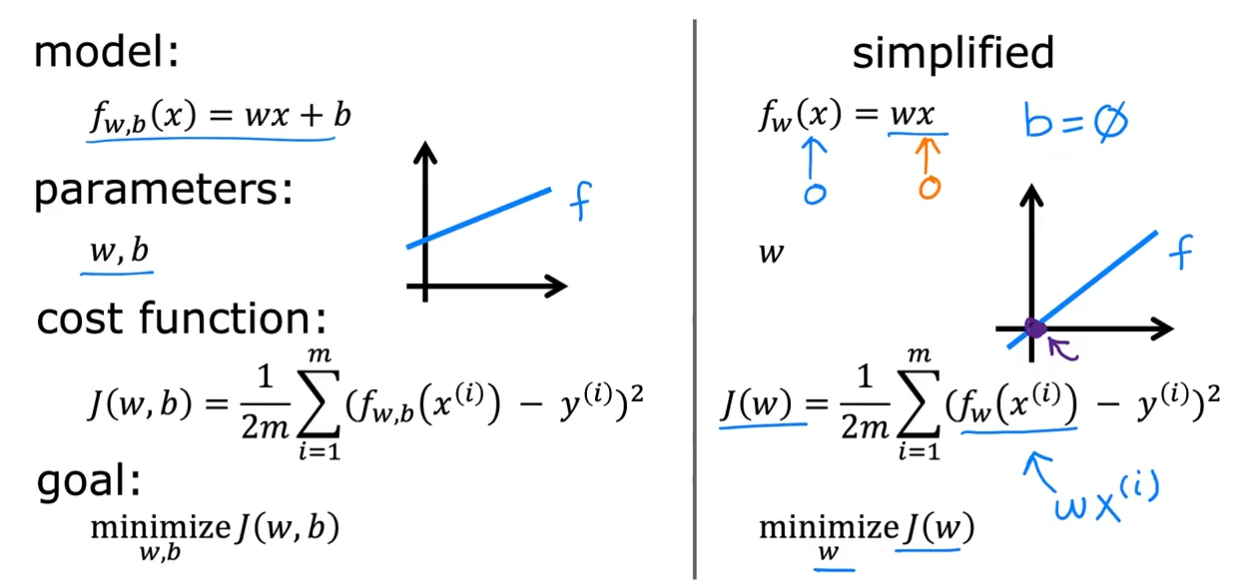
对于一个$ f_{w,b}(x) $的模型来讲，我们需要调整它的参数$ w,b $使得找到代价函数$ J{(w,b)} $的值最小，在数学中我们常常将其写为$ \underset{w,b}{\operatorname*{minimize}}J(w,b) $代表找到$ w,b $使得$ J $尽可能的小。为了更好的看到变化，我们将$ b $设置为$ 0 $使得可以更好的看到图像的不同。

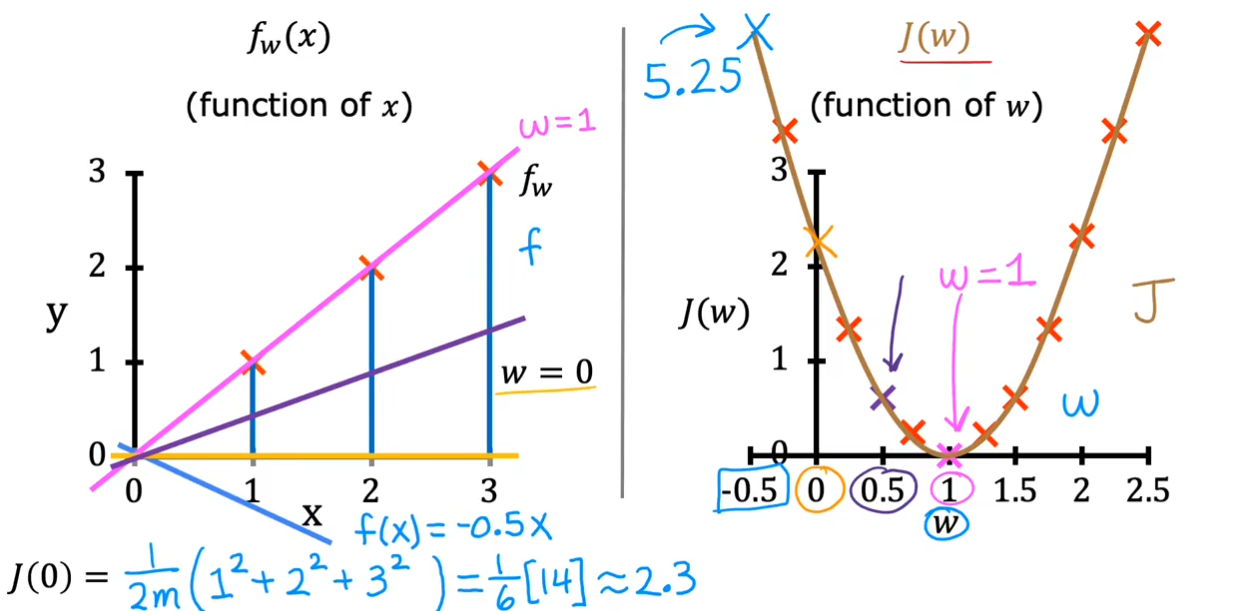
可以看到在图中训练集的情况下，选择$ w = 1 $得到的$ J(w,b) $最小。

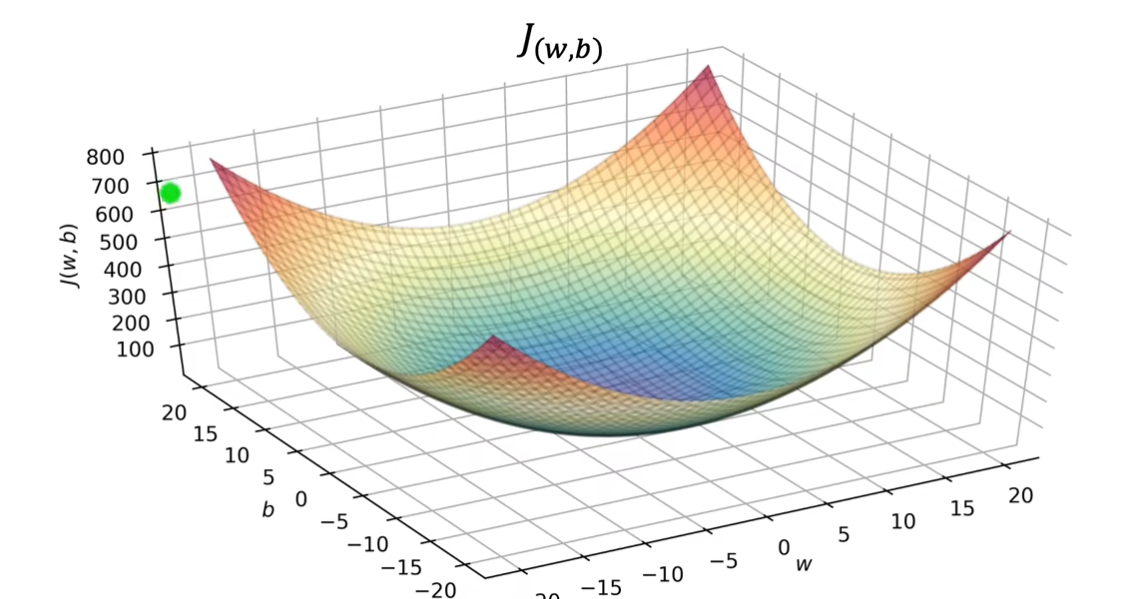
现在让我们重新考虑起$ b $，那么就会得到一个3D碗状的等高线图。

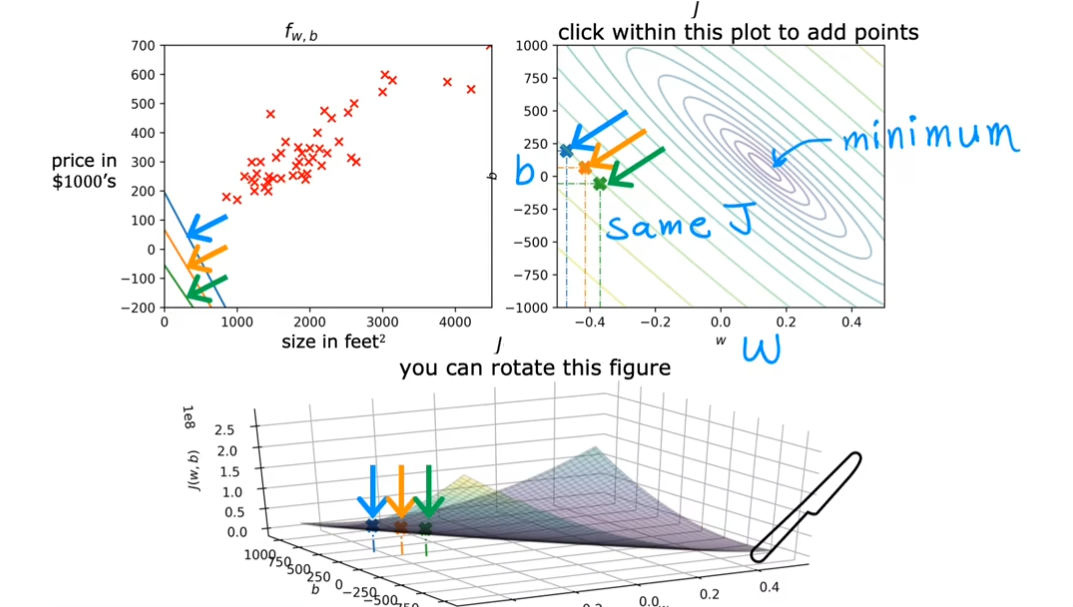
如果将这个图从水平切开，那么也就会得到右上角的图。